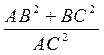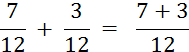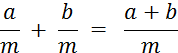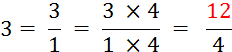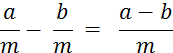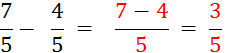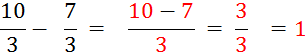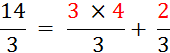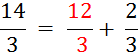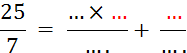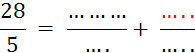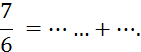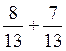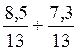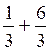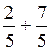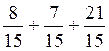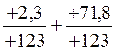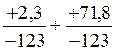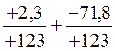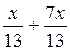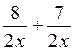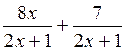|
Niveau VI et V |
|
||
|
|
|
|
|
|
|
|
Allez vers le corrigé… |
Pré requis :
Expression
d' un résultat
|
|
ENVIRONNEMENT du dossier :
|
|
|
|
|
|
|
Objectif précédent |
Objectif suivant :…. |
|
DOSSIER : ADDITION (
somme)
et SOUSTRACTION (différence) de nombres en écriture fractionnaire et factions
|
|
Fiche 1 : ADDITION : Somme de nombres
en écriture fractionnaire. |
|
|
|
Fiche 2 : Exercices sur l’addition dont intervient ,au moins, une fraction ou écriture
fractionnaire. |
|
|
|
Fiche 3 : SOUSTRACTION : différence de nombre
sous forme d’une écriture fractionnaire. |
|
|
|
Fiche 4 : Partie entière d’un nombre sous
forme d’une écriture fractionnaire. |
|
|
|
Fiche 5 :
Situations problèmes. ( pour ceux qui veulent
se mesurer ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Interdisciplinarité : 2°) Algèbre |
|
||||||
|
|
|
|
Ne faire les calculs
qu’en lien avec l’objectif !! |
|
|
|
|
Définition de l’objectif: Savoir additionner
deux fractions ayant le même dénominateur
|
|
|
|
||||||
|
|
Fiche 1 : Somme de nombres en écriture
fractionnaire. |
|
|
|||||
|
|
|
|
||||||
|
|
Cas particulier de fractions décimales. |
|
||||||
|
|
|
|
||||||
|
|
Complétez
« Vous concevez alors que l’on puisse écrire « Nous allons étendre cette addition aux fractions qui
ne sont pas décimales. |
|
||||||
|
|
Exemple avec des fractions : |
|
||||||
|
|
( avec des dénominateurs dont la valeur est différente de 10) |
|
||||||
|
|
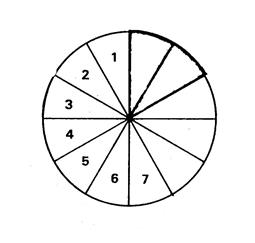
Considérons une tarte partagée en 12 portions
identiques. Complétez la numérotation…… |
|
|
|||||
|
|
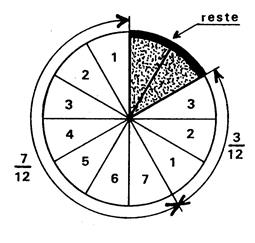
On a d’abord consommé « 7 » portions , puis une deuxième fois « 3 » portions
sont consommées. Le nombre de portions consommées est de : 7 + 3 = ….10 … Chaque portion représente « La première fois
il a été consommé les La deuxième fois il a été consommé les |
|
|
|||||
|
|
Au total il a été consommé sept douzièmes plus
trois douzièmes de la tarte. C'est-à-dire dix
douzième de la tarte. |
|
||||||
|
|
On écrit alors |
|
|
|||||
|
|
On dit alors que
|
|
||||||
|
|
|
|
||||||
|
|
Ce qui
vient d’être fait avec On dira alors : |
|
||||||
|
|
A
retenir : |
|
||||||
|
|
« a », « b » et
« m » étant des nombres décimaux , avec « m |
|
|
|||||
|
|
Ce qui se traduit : La somme de deux fractions de même dénominateur est égale à une
troisième fraction qui a : -
pour
« numérateur » la somme des numérateurs, et -
pour
« dénominateur » : le dénominateur commun. |
|
||||||
|
|
|
|
||||||
|
|
Activités n°…… |
|
||||||
|
|
Calculez : |
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
||||||
|
|
Situation problème n°1 |
|
||||||
|
|
Ce weekend , vous avez fait vos devoirs et vous
avez appris vos leçons. Vous avez consacré Combien de temps avez-vous travaillé ? |
|
||||||
|
|
Corrigé :
|
|
||||||
|
|
Situation problème n°2 |
|
||||||
|
|
Lors d’élections, deux candidats se présentent. -
Le premier recueille
« 56 % » des voix des électeurs inscrits. -
Le deuxième recueille
« 24 % » des voix des électeurs inscrits. Quel est le pourcentage des électeurs votants par
rapport aux électeurs inscrits ? (exprimez les pourcentages en fractions) |
|
||||||
|
|
« 56 % = |
|
||||||
|
|
|
|
|||
|
|
Fiche 2 : Exercices sur l’addition dont
intervient, au moins une fraction ou écriture fractionnaire. |
|
|||
|
|
|
|
|||
|
|
Cas 1 : dénominateurs différents : |
|
|||
|
|
Dans le cas où les écritures fractionnaires n’ont
pas le même dénominateur , on les remplace par des
écritures de même dénominateur. |
|
|||
|
|
|
|
|||
|
|
Exemple : on vous demande de calculer : On a alors : |
|
|||
|
|
Activités n°… |
|
|||
|
|
1°) Calculez :
|
|
|||
|
|
|
|
|||
|
|
2°) Calculez
: |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
3°) Calculez
: |
|
|||
|
|
|
|
|||
|
|
3°) Faites de même avec :
|
|
|||
|
|
|
|
|||
|
|
Cas 2 : Somme de deux termes avec un nombre entier naturel et une
fraction : |
|
|||
|
|
|
|
|||
|
|
1°) On vous demande de calculer :
|
|
|||
|
|
Donc : |
|
|||
|
|
|
|
|||
|
|
Activités n°…. |
|
|||
|
|
2°) Faîtes de même pour : |
|
|||
|
|
Transformons « 6 » en
fraction de dénominateur « 7 » : Aussi : |
|
|||
|
|
3°) Faîtes de même pour : |
|
|||
|
|
Transformons « 5 » en
fraction de dénominateur « 5 » : Aussi : |
|
|||
|
|
4°) Faîtes de même avec : |
|
|||
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
|||||
|
|
Fiche 3 : SOUSTRACTION : différence de
nombre sous forme d’une écriture fractionnaire. |
|
|||||
|
|
|
|
|||||
|
|
Approche : |
|
|||||
|
|
Complétez : « Or on peut écrire que : Vous concevez alors que l’on puisse écrire
que : |
|
|||||
|
|
Nous pouvons appliquer cette définition à tous nombres « x » , « y » et « z » en écriture
fractionnaire. « x – y = z »
signifie que « x = z + y » |
|
|||||
|
|
|
|
|||||
|
|
Vous venez de voir que : On peut donc écrire que |
|
|||||
|
|
|
|
|||||
|
|
A retenir : |
|
|||||
|
|
« a », « b » et
« m » étant des nombres décimaux
( dit : non relatifs) donc « a |
|
|
||||
|
|
Ce qui se traduit : La différence de deux
fractions de même dénominateur est égale à une troisième fraction qui
a : -
pour
« numérateur » la différence
des numérateurs, et -
pour
« dénominateur » : le dénominateur commun. |
|
|||||
|
|
Remarque : la fraction sera
précédée du signe « + » (positive) si « a |
|
|||||
|
|
|
|
|||||
|
|
Activité n°….. |
|
|||||
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
Dans le cas où les écritures fractionnaires n’ont
pas le même dénominateur , on les remplace par des
fractions ( écritures fractionnaires) ayant le même dénominateur. |
|
|||||
|
|
|
|
|||||
|
|
Complétez : |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
Activité n°… |
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||||||||||||
|
|
Fiche 4 Partie entière d’un nombre sous forme
d’une écriture fractionnaire. |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Considérons le nombre : Vous savez que |
|
1 |
4 |
3 |
|
|
||||||||||
|
- |
1 |
2 |
4 |
||||||||||||||
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
· « 4 » est appelé la « partie
entière » de · « 4 » est le quotient entier approché par défaut de « 14
par 3 » |
|
|||||||||||||||
|
|
Par encadrement , la fraction est compris entre …….. On peut écrire que |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
· En considérant la division de « 4 par 3 »
, on peut écrire : « 14 = 3 · Ce qui permet d’écrire que :
|
|
|||||||||||||||
|
|
Or vous savez que : |
on écrira alors : |
|
|
|||||||||||||
|
Mais comme |
On écrira alors : |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Ainsi :
Puisque « 2 » est le reste de la
division et « 3 » le diviseur , alors « 2 Il en serait de même pour tout nombre écrit sous
forme fraction. ! |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Activité n°… |
|
|||||||||||||||
|
|
1°) Ecrire
comme ci-dessus : |
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
2°) Faîtes apparaître le nombre d’heures ( entières ) dans
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Comparaison de nombres en écriture fractionnaire. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
On vous demande de comparer les deux fractions : 1°) on va comparer les parties entières : La partie entière
de Puisque « 4
|
|
|||||||||||||||
|
|
Activités n°… |
|
|||||||||||||||
|
|
Comparer les fractions : |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||||||
|
|
Droite graduée. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Pour placer , sur une
droite graduée, un point dont on donne l’abscisse , sous forme d’une fraction
, , il est commode de déterminer la
partie entière de ce nombre . Cela nous permet de le situer entre deux entiers
consécutifs. |
|
|||||||||||||||
|
|
Exemple : Pour placer le point d’abscisse Ecrit autrement : |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Activités n° …. |
|
|||||||||||||||
|
|
Placez de même
sur la droite ci-dessous les points d’abscisses : |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Fiche 5 :
Situations problèmes. ( pour ceux qui veulent
se mesurer ) |
|
|
|
|
|
|
|
N°1 : |
|
|
|
Avec une bouteille contenant SI « oui » quelle fraction de litre reste-il dans la
bouteille ? Si « non » quelle fraction de litre manque-t-il pour
remplir la carafe ? |
|
|
|
|
|
|
|
N° 2 : |
|
|
|
Une personne doit rembourser une somme d’argent
en 3 ans. La première année elle rembourse les Quelle fraction de la somme lui reste-il à rembourser ? |
|
|
|
|
|
|
|
N° 3 : |
|
|
|
Un réservoir est plein. On en retire le Quelle est la contenance de ce réservoir ? |
|
|
|
|
|
|
|
N°4 : |
|
|
|
La journée d’une certaine personne est répartie
de la manière suivante :
Le reste est consacré aux loisirs. Quelle fraction de la journée représentent les
loisirs ? |
|
|
|
|
|
|
|
N° 5 : |
|
|
|
Tu veux acheter un lecteur MP3. La somme que je possède n’est que le On me donne « 100 € »
. Vous possédez alors les Quel est le prix de ce lecteur ? |
|
|
|
|
|
|
|
N° 6 : |
|
|
|
Un bassin peut être vidé par deux robinets. Le premier robinet vide le bassin en « 8 h »,
le deuxième le vide en « 10 h ». 1°)Quelle fraction du
bassin est vidée en « 1 h »quand les robinets sont ouverts ensemble ? 2°) Combien faut-il de temps (
en h ; mn ; s ) pour
vider le bassin dans cette situation ? 3°) le bassin est rempli normalement en « 6
h ». On oublie de fermer le premier robinet ( le deuxième est fermé) . Combien de temps faudra-t-il pour remplir le réservoir ?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Par exemple : on peut faire l’opération: 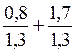 qui
donnera
qui
donnera ![]()
![]()
TRAVAUX auto
formatifs :
Info pédagogique :Le niveau de
« compétences » pour un élève de 6ème n’est le même qu’un élève de 3ème ;
pour chaque classe on consultera le référentiel.
1°)
L’addition de deux fractions (ou écriture fractionnaire )
n’est possible qu ’ à une condition laquelle ?
2°)Traduire
en langage littéral: 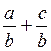 =
=![]()
3°)Traduire
en langage mathématique:
La somme de deux
fractions est égale à une troisième fraction qui aura pour :Numérateur
la somme des numérateurs et pour Dénominateur le dénominateur commun.(En
utilisant d’autres lettres que a ; b ; c )
4°)Donner
la procédure permettant de faire l’addition de deux fractions de même
dénominateur.
Niveau VI:
Effectuer les calculs suivants:
|
|
|
|
|
|
Niveau VI et V:
|
|
|
|
|
Niveau V : Faire exercices avec des nombres décimaux relatifs .
|
|
|
|
Niveau III:
Algèbre ; Faire les
additions suivantes
|
|
|
|
Trigonométrie : faire la somme : ![]() avec
avec ![]()
Réponse :