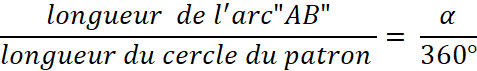|
|
|
Classe de
Troisième ( P 3) |
|
|
|
|
|
|
|
Pré requis |
|
|
|
|
Le triangle |
|||
ENVIRONNEMENT du
dossier:
DOSSIER :
Fiches sur : LE CÔNE de
révolution et le tronc de cône. :
|
|
Fiche 1 : Cône de révolution et tronc de cône. |
|
|
|
Fiche 2 : Calcul dans le cône de révolution. |
|
|
|
Fiche
3 : Calcul des dimensions d’un patron de cône. |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
Fiche 1 : Cône de révolution et tronc de cône.
|
|
|
|
|
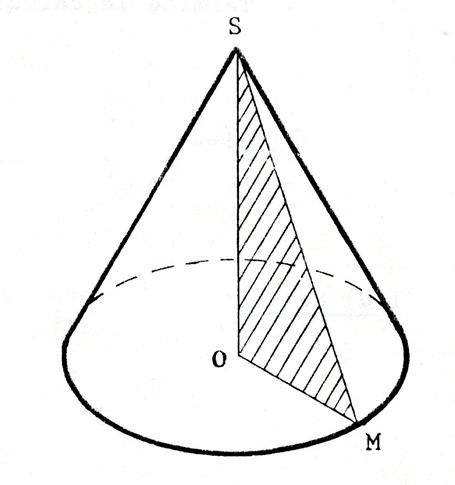
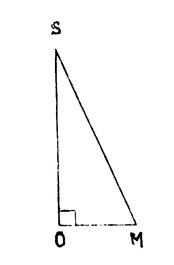
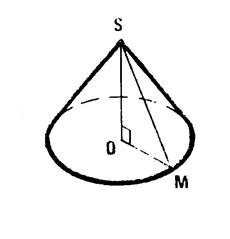
Ci-contre
on vous donne un dessin qui représente en
perspective cavalière un cône de révolution. « S »
est le sommer du cône. Sa base
est un disque . « O » est le centre du
disque. [ SO ] est
hauteur. ( SO)
est l’axe du cône. ( SO ) est perpendiculaire au plan de base. [ OM ] étant un rayon du disque de basez, ( SO ) est perpendiculaire à ( OM ), le
triangle « SOM » est donc un triangle rectangle. |
|
|
|
|
Expliquez pourquoi (verbalement) la longueur
« SM » est toujours la même quelle que soit la position de
« M » sur le cercle de base. On dit que le cône est engendré par le triangle
« SOM » tournant autour de l’axe (SO). « Faire un tour complet » se dit aussi « faire une
révolution », d’où le nom de « cône de révolution ». Le segment [ SM ] est
appelé « génératrice ». En tournant, il engendre la surface latérale du
cône. |
|
|
|
|
Intersection d’un cône de révolution par un plan parallèle à la base. |
|
|
|
|
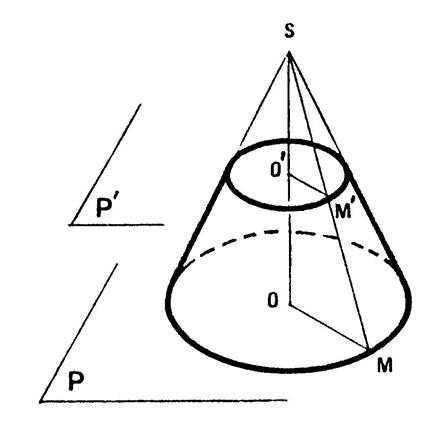
Ci-contre un cône « C » de sommet
« S ». « O » est le centre du disque de base . « P » est plan de la base.
« P’ » est un plan parallèle à « P ». Il est possible de démontrer que l’intersection
du cône « C » par le plan « P’ » est un disque dont le
centre est sur « (SO ) » Le plan « P’ » partage le cône
« C » en un cône « C’ » et un « tronc de cône » . Le cône « C’ » apparaît comme une
réduction de « C ». |
|
|
|
|
|
|
|
|
|
Fabrication d’un cône révolution et d’un tronc de cône. |
|
|
|
|
|
|
|
|
|
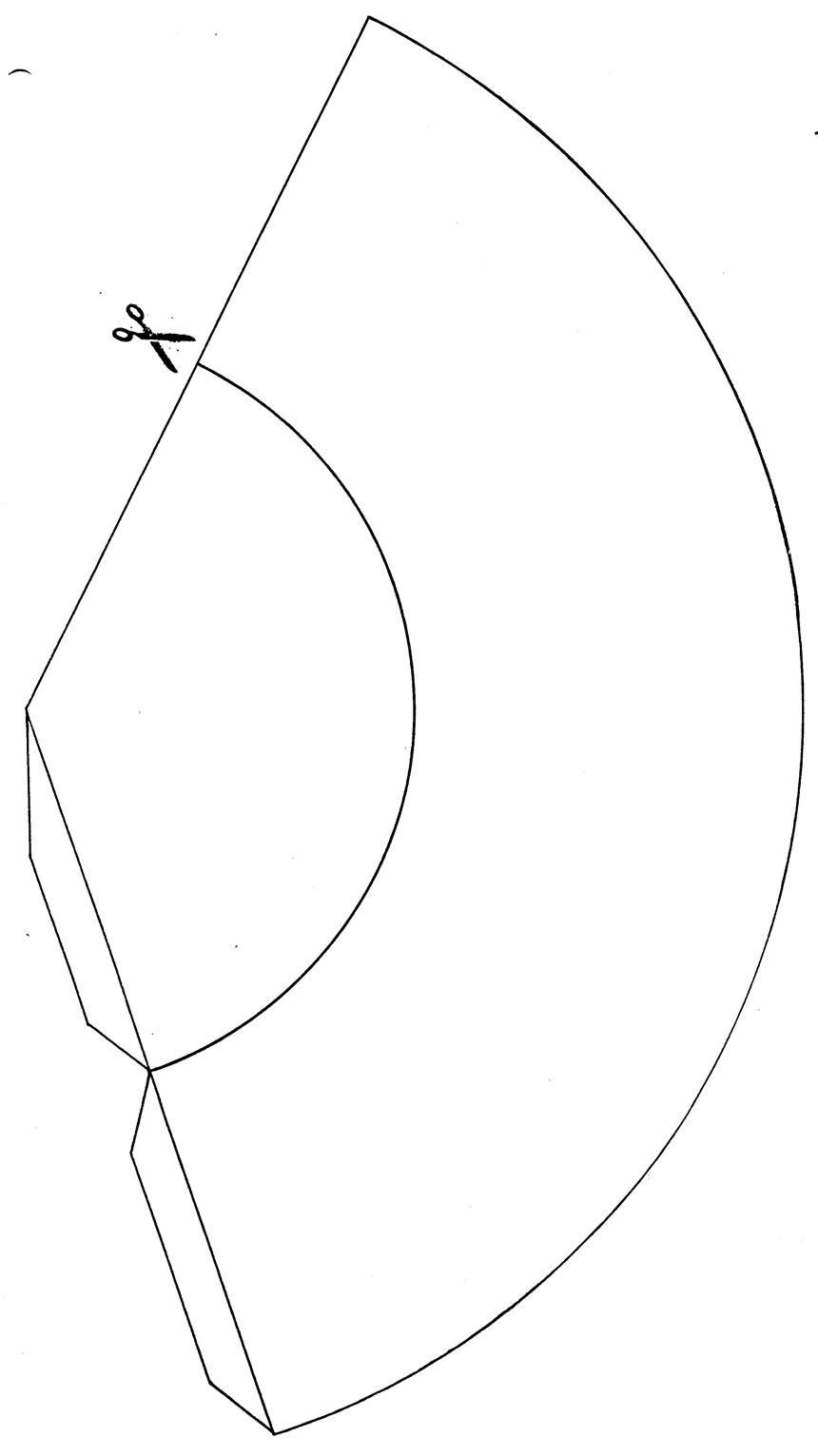
Prenez la dernière page de ce dossier (Page patron ( fiche
1 ) ) ;, découpez le patron du cône « C’ » et du tronc de cône.
, puis faites les collages nécessaires pour obtenir ces deux solides. Vous pouvez vérifier en plaçant convenablement le
cône « C’ » sur le tronc de cône que l’on obtient bien le cône
« C ». |
|
|
|
|
|
|
|
|
|
Fiche 2 : Calcul dans le cône de révolution. |
|
|
|
|
|
|
|
|
|
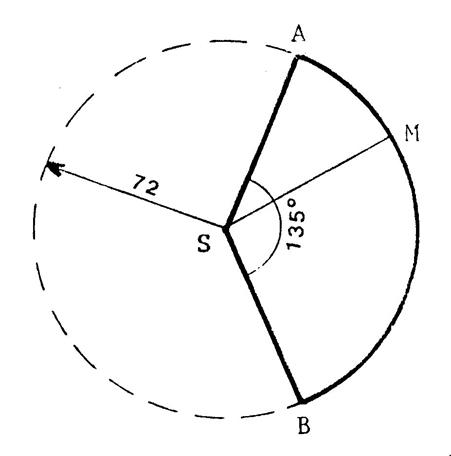
Nous reprenons le cône « C’ » et son
patron. Le patron est un secteur de disque de 72 mm de
rayon et dont l’angle est égal à 135° . Nous allons calculer le rayon « R » de
la base , la hauteur « h » , l’ aire
latérale et l’angle du cône. A ) Calcul du rayon « R ». La longueur du cercle de base du cône est égale à
la longueur de l’arc La longueur du cercle de base est égale
à : |
|
|
|
|
La longueur de l’arc Elle est les La longueur du cercle entier est égale à : |
|
|
|
|
La longueur de l’arc On a alors
|
C'est-à-dire : |
|
|
|
|
|
|
|
|
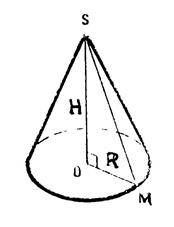
B ) Calcul de la hauteur « H » |
|
|
|
|
« M » étant un point quelconque du
cercle de base , le triangle « SOM » est
un triangle …………….. (
voir la fiche n° …..) Grâce au théorème de Pythagore
, on peut écrire :
SO² = SM ² - OM ² Or « SM » est égal au rayon du disque
du patron donc : SM =
……………………mm Terminez le calcul : H ² = ……………… |
|
|
|
|
|
|
|
|
|
C ) Calcul de l’aire de la surface latérale. |
|
|
|
|
C’est les |
|
|
|
|
|
|
|
|
|
D ) Calcul de l’angle du cône. |
|
|
|
|
On appelle « angle de cône » le double
de l’angle
Continuez le calcul de donner le résultat à 1° prés . |
|
|
|
|
|
|
|
|
|
Fiche 3 : Calcul des dimensions d’un patron
de cône. |
|
|
|
|
|
|
|
|
|
Calcul du rayon . Le patron est un secteur de disque dont le rayon
est égal à la longueur de la génératrice [ SM ] du cône. Dans le triangle « SOM » rectangle en
« O » , vous pouvez calculer
« SM ». |
|
|
|
|
|
|
|
|
|
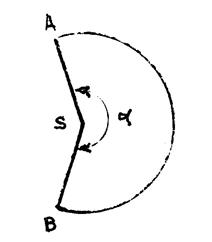
Calcul de l’angle. Nous appelons «
La longueur de l’arc « AB » est égale à
la longueur du cercle de base du cône. |
|
|
|
|
Cette longueur est égale à : …………………….( Donnez la relation , n’effectuez pas le calcul ) Longueur du cercle du patron : …………………….( Donnez la relation , n’effectuez pas le calcul )
|
|
|
|
|
Page patron ( fiche 1 ) |
|
|
|
|
Base du petit cône. |
|
|
|
|
|
|
|
|
|
Base pour le tronc de cône. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|