Cette fiche de travail  va  vous permettre de différencier chez le quadrilatère  le rectangle et des autres figures à quatre côtés ….. de bases 

1°) La définition du rectangle.

2°) Les propriétés du rectangle.

« les diagonales » et « symétries »

3°) Récapitulatif des propriétés d’un rectangle.

Tout d’abord voyons la définition du rectangle !!!!

1°) La définition du rectangle.

Nous avons déjà vu que :

Un quadrilatère est « un rectangle » ce qui signifie que :

Ses côtés opposés sont parallèles et ses côtés consécutifs sont perpendiculaires.

Cet énoncé, que nous appelons « une définition », nous donne les informations suivantes :

·       Info 1 : nous avons le nom de l’objet mathématique considéré : le quadrilatère.

·       Info 2 : On nous dit comment  reconnaître un tel objet :

Ainsi, on peut affirmer qu’un quadrilatère est un rectangle à condition d’être certain que :

o   Ses côtés opposés soient :  …… « parallèles »…………………..

o   Ses côtés consécutifs soient ……… « perpendiculaires »………………………….

Autrement dit : Si on sait qu’un quadrilatère a ces deux propriétés, alors on peut affirmer que ce quadrilatère est un «  rectangle »..

Sous-entendu : Si un quadrilatère n’a pas à la fois ces deux propriétés, alors …………………………………………….

·       Info 3 : l’énoncé nous nomme  des  propriétés que possède un tel objet :

Si on sait qu’un quadrilatère est un rectangle , alors on peut affirmer que :

o   Ses côtés opposés  sont  « parallèles » …

o   Ses côtés consécutifs  sont  « perpendiculaires » ….

Mais  le rectangle a  d’autres propriétés ………………..

Entre autre, vous savez que tout rectangle que tout rectangle possède deux axes de symétries .

Dans les chapitres suivants, vous allez chercher d’autres propriétés du rectangle et d’autres façons de reconnaître un rectangle.

Activité n°1 :

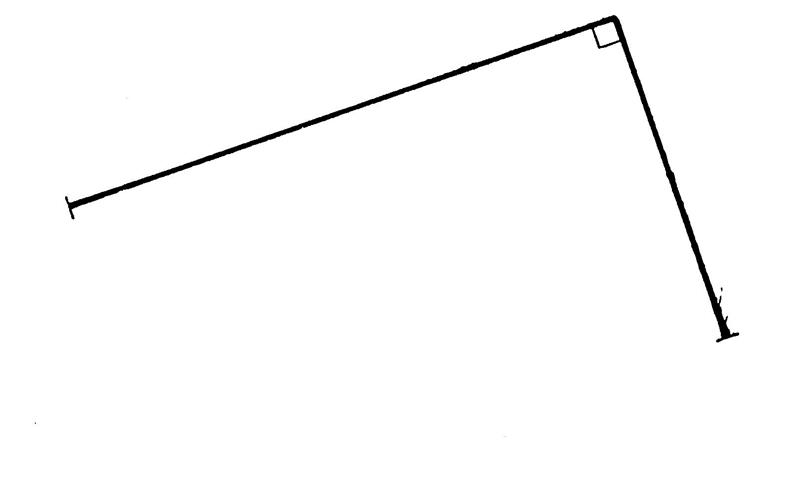
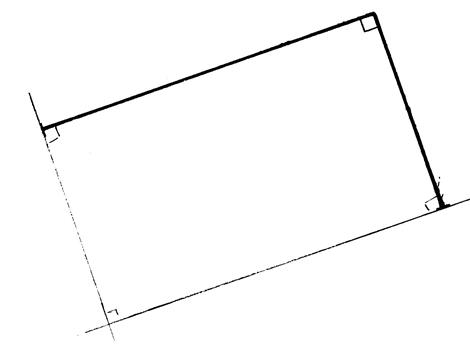
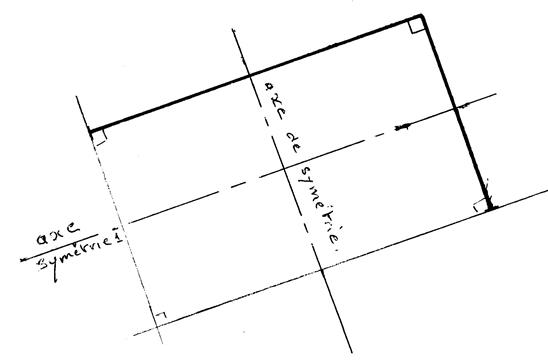
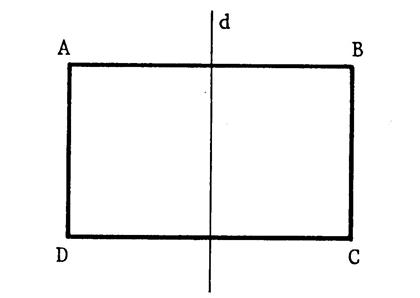
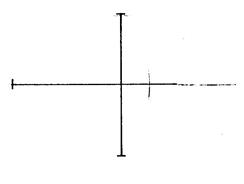
On vous a dessiné, ci- dessous, deux côtés d’un rectangle.

On vous demande de dessiner les autres côtés et de tracer les axes de symétries de ce rectangle.

Corrigé

2°) Les propriétés du rectangle.

Activité n°2 :

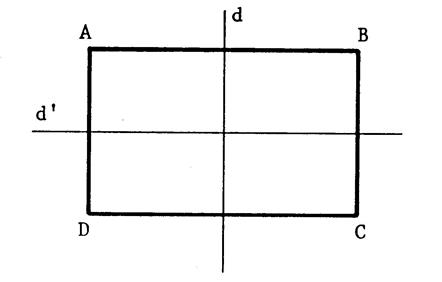
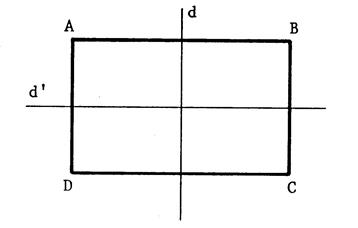
Prenez une feuille de calque ( format 21 x29,7)  , de la forme de la figure ci-contre ..

o   Nommez les sommets « A », « B »,  « C », « D » ; c’est un rectangle.

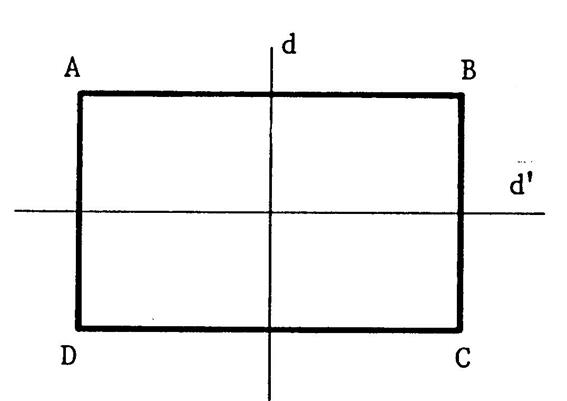
o   Pliez cette feuille pour obtenir les droites « d » et « d’ »

Info :   « d » et « d’ » sont ses axes de symétrie.

Vous constatez que [ A D]  coïncide avec …[ BC ]  …

Donc [ A D]  et  [ BC ]  ont même    « mesure »….

On peut dire que  « AD  …=  ….BC »….

·       En pliant suivant la droite « d’ » on obtiendrait de même :

« AB  …=  ….DC »….

Il en est ainsi pour tout rectangle, on peut donc dire

A retenir :

Dans un rectangle, les côtés opposés ont même  mesures.

Activité n°3 :

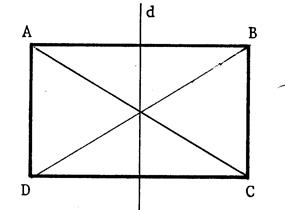
o   Reprenez  la feuille de calque ci-dessus : et sur la figure ci-contre.

Tracez les diagonales  [ A C]  et  [ BD ]  du rectangle. ; celles-ci se coupent en « O »

Nous considérons la symétrie orthogonale d’axe « d ».

o   Vérifiez que « B » est  le symétrique de « A » par rapport à la droite« d ».On dit que .« A » a pour symétrique  «  B » ..

o   Vérifiez que « D » est  le symétrique de « C » par rapport à la droite« d ».On dit que «  C »  a pour symétrique   «D ».. 

(Cette partie est difficile à comprendre, je vous conseille faire l’ exercice sur une feuille libre et dessinez  le tracé de la symétrie orthogonale de la droite AC par rapport a « d »  qui est « BD »)

On peut dire que : Le segment [ AC ] a donc pour symétrique  ………[ BD ]  ……

Les segments [ AC ]  et [ BD ]  étant symétriques ont donc même .. « Mesure »..

o   Tracé des diagonales 

Corrigé : tracé du cetntre « O »

o  

On dira alors :

(à retenir)                           Dans tout rectangle, les diagonales ont même mesure.

Remarque : On vient ainsi de prouver par le raisonnement, une propriété que vous avez constatez approximativement  en mesurant.. ( voir le cours sur les polygones)

Activité n°4 : 

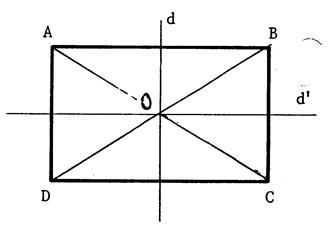
·       Nous appelons « O » le point d’intersection des droites ( A C )  et  ( B D ) . On vous demande de compléter le calque et la figure ci-dessous.

a)      Considérons de nouveau la symétrie orthogonale d’axe « d ».

« A » a pour symétrique …… « B »…. Et  « C » a pour symétrique … « D »…donc la droite « AC » a pour symétrique la droite ………..

Etant à la fois sur ( A C ) et sur ( B D ) , le point « O » est alors son propre symétrique.
Donc   le point « O » est situé sur « d ». ( voir centre de symétrie)

Et : dans une symétrie orthogonale :

[ OA ]  a pour symétrique  [ OB ]  , donc OA ….=….. OB .

[ OC ]  a pour symétrique  [ OD ]  , donc OC….=….. OD .

b)    Considérons la symétrie orthogonale d’axe « d ’ ».

Vous trouverez de même que « O » est situé sur … « d’ »…et que OA = …OD. Et OC = … « OC »

Vérification : pliez le calque suivant la droite « d’ ».

En considérant les 4 égalités , vous pouvez  écrire : OA = OB = OC = OD

Ce qui vous permet d’affirmer que « O » est le ……………..centre de gravité………….de [ AC ] et de   [BD]

A retenir :

Dans tout rectangle les diagonales se coupent en leur milieu.

Remarque :

Puisque : OA = OB = OC = OD

On peut affirmer que « A » , « B » , « C », « D » sont situés sur un ………….de centre …………

Tracez le sur le dessin…

3°) Récapitulatif des propriétés d’un rectangle.

Si  vous savez qu’un quadrilatère est un rectangle, alors vous pouvez affirmer qu’il possède les 5  propriétés suivantes :

Propriété n°1 :

« P₁ » Les côtés opposés sont parallèles.

Propriété n°2 :

« P₂ » Les côtés consécutifs sont perpendiculaires.

Propriété n°3 :

« P₃ » Les opposés ont même longueur.

Propriété n°4 :

« P₄ » Les diagonales ont même longueur.

Propriété n°5 :

« P₅ » Les diagonales se coupent en leur milieu.

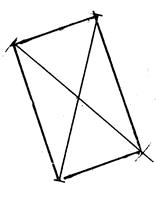
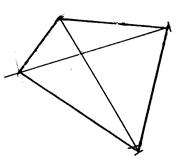
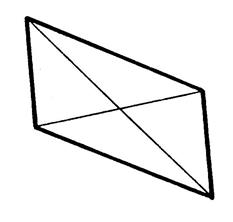
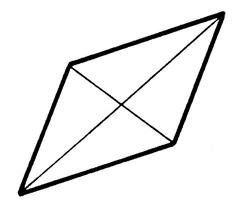
Activité 5  : Est-ce un rectangle ?

Si un quadrilatère possède une ou plusieurs de ces 5 propriétés peut-on dire que c’est un rectangle ?

Activité 5-A )  Un quadrilatère qui possède la propriété « P₁ » est-il rectangle ?

Propriété P1 :  Les côtés opposés sont parallèles.

Figure « a »

Figure « b »

Figure « c »

Figure « d »

Vérifiez que les 5  quadrilatères  ont leurs côtés opposés parallèles.

Reconnaissez-vous  les figures qui sont des rectangles ?:

………………………………………….

……………………………………………

Figure « e »

Vous voyez donc que la propriété  ( P1) « avoir ses côtés opposés parallèles »  n’est pas suffisante pour qu’un quadrilatère soit un rectangle.

Activité 5-B )  Un quadrilatère qui possède la propriété « P₂ » est-il rectangle ?

Propriété P₂ :  Les côtés consécutifs  sont perpendiculaires.

« à votre avis », est ce obligatoirement un rectangle ?  Appelons « ABCD » ce quadrilatère.

Grâce à la propriété « P₂ » qu’il possède, on peut écrire.

( A B ) ⏊ ( BC ) , ( BC ) ⏊ ( CD ) , ( DA ) ⏊ ( BC ) , ( DA ) ⏊ ( AB ) .

Or, puisque les droites (AB) et ( DC) sont toutes les deux « perpendiculaires » à ( BC ).

Alors elles sont « parallèles ». (info ++)

On  prouverait de même que ( AD)  et ( BC ) sont ………parallèles….

On peut donc affirmer que ce quadrilatère possède non seulement la propriété « P₂ » mais aussi la propriété « P₁ »

Donc d’après ce que l’on a vu au premier chapitre ce quadrilatère est bien un …….« rectangle »…..

On retiendra :

Un rectangle est un quadrilatère qui a ses côtés consécutifs  perpendiculaires.

Activité 5-C )  Un quadrilatère qui possède la propriété « P₃ » est-il rectangle ?

Propriété P₃ :  Les côtés opposés ont même longueur.

On vous propose cinq figures……

Figure « a ».

Figure « b ».

Figure « c ».

Figure « d ».

Vérifiez que les 5 quadrilatères ont leurs côtés opposés ont la même longueur.

Reconnaissez ceux qui sont des rectangles.

Vous voyez donc que la propriété « avoir ses côtés opposés de même longueur » n’est pas suffisante pour qu’un quadrilatère soit un rectangle.

Figure « e ».

Parmi les propriétés « P₁ » , « P₄ » , « P₅ », laquelle à votre avis, faut-il adjoindre à « P₃ » pour que le quadrilatère soit un rectangle. ?.............................

Nota : on ne considère pas la propriété « P₂ » car à elle seule elle suffit pour que le quadrilatère soit un rectangle.

Activité 5-D )  Un quadrilatère qui possède la propriété « P₄ » est-il rectangle ?

Propriété P₄ :  « P₄ » Les diagonales ont même longueur.

On ne considère ici que des quadrilatère convexes.

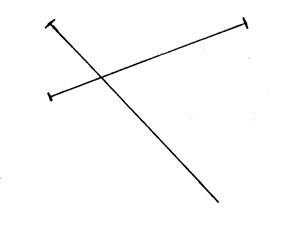
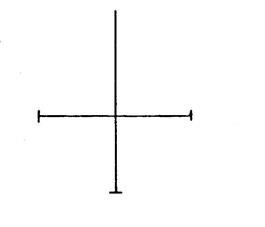
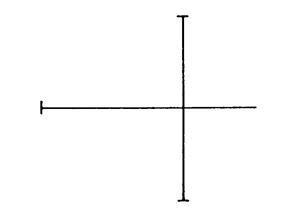
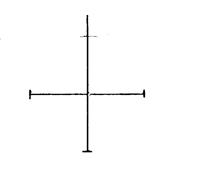
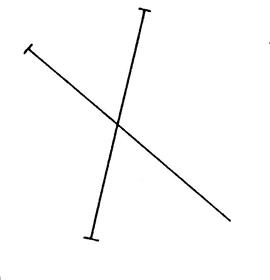
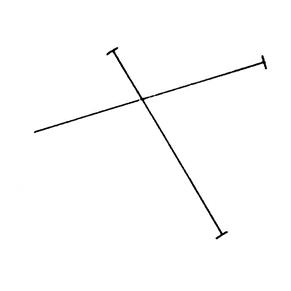
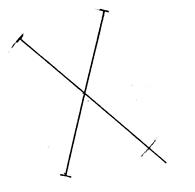
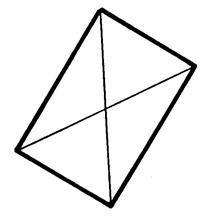
Dans les cinq exemples ci-dessous, on a placé « 3 » des « 4 » sommets d’un quadrilatère et le support des diagonales.

Activité n°…..  : On vous demande de placer le quatrième sommet de telle sorte que les diagonales aient la même longueur.

Tracez ensuite les côtés de ces quadrilatères.

Figure « a »

Figure « b »

Figure « c »

Corrigé

Corrigé

Corrigé

Figure « d »

Figure «e »

Complétez les  cinq figures proposées et entourez ceux qui sont des rectangles. .

Corrigé

Corrigé

Activité 5-E )  Un quadrilatère qui possède la propriété « P₅ » est-il rectangle ?

Propriété P₅ :  « P₅ » Les diagonales se coupent en leur milieu.

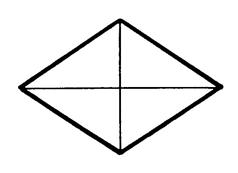
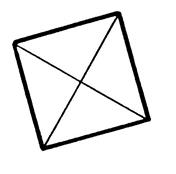
Activité n°… : Vérifiez que ces quadrilatères ont les diagonales qui se coupent en leur milieu.

Reconnaissez ceux qui sont rectangles. les entourer ..

Figure « a »

Figure « b »

Figure « c »

Corrigé c’est un rectangle

Figure « d »

Figure « e »

Entourez les rectangles…....

Corrigé c’est un rectangle

Vous voyez donc que la propriété « avoir ses diagonales se coupent en leur milieu »  n’est pas suffisante pour qu’un quadrilatère soit un rectangle.

Parmi les propriétés « P₁ »,  « P₃» , « P₄ », laquelle à votre avis, faut-il adjoindre à « P₅ » pour que le quadrilatère soit un rectangle.

  «  P ₄ » les diagonales ont mêmes longueurs