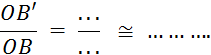Fiche 1 : Opérateur de projection .

Fiche 2 : Projection orthogonale.

Fiche 3 : Cosinus de l’angle aigu de deux droites.

Fiche 4 : Exercices .

Fiche 5 : Fabrication d’une table de cosinus.

Fiche 6 : Représentation graphique ….

Fiche 7 : Dans le triangle rectangle.

Fiche 8 : Construction d’un angle connaissant son cosinus.

Fiche 9   Exercices .

Fiche 1 : Opérateur de projection .

Info @ plus.

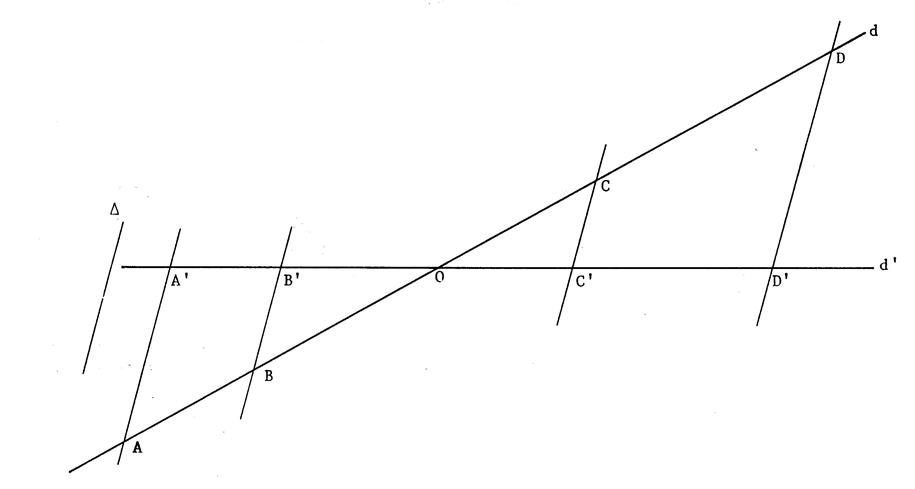
On donne deux droites «  »  et «  » se coupant en « ».

On projette «  » sur «  » suivant la direction «  » .

Activité n°1.

1°)  On vous demande de mesurer sur la figure les segments (sur la droite « d »)  et leurs projetés respectifs. (sur la droite « d’ ») 

Inscrire les valeurs (nombres) dans le tableau ci-dessous.

 2°) Calculer les quotients (divisions) , conservez deux chiffres après la virgule.

Segment projeté.

[ O A ]

[ O B ]

[ O C ]

[ O D ]

[ AB ]

[ AD]

[ O E ]

[ O F ]

Mesure du segment

78

Mesure du projeté .

58

0,74

Choisissez sur « d » deux autres points : « E » et « F » et faîtes comme pour « A »,  « B », « C » , « D ».

Vous constatez que l’on trouve sensiblement le même quotient dans tous les cas.

Il est possible de faire une démonstration prouvant que ces quotients sont égaux.

On peut écrire :

·       « opérateur de projection »

                   Le nombre représenté par tous ces quotients est appelé  « opérateur de projection ».

                   Il ne dépend pas des points choisis sur les droites «  » et «  ».

                   Il dépend de la direction de projection et de l’angle aigu des deux droites.

·       D’après ce qui précède , on peut dire qu’il y a proportionnalité entre la longueur d’un segment et la longueur de son projeté.

Le coefficient de proportionnalité n’est autre que  l’opérateur de projection.

Fiche 2 : Projection orthogonale.( et projection oblique)

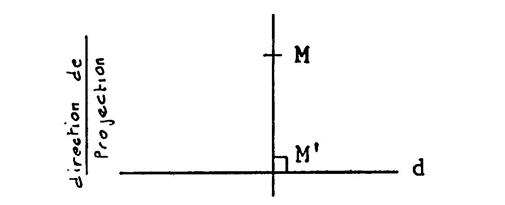
                  Une projection orthogonale  est une projection dans laquelle la direction de projection est orthogonale à la direction de la droite sur laquelle on projette.

C'est-à-dire : toutes les projetantes sont  parallèles  à la droite sur laquelle on projette.

ci-dessous : la projection orthogonale  de « M »

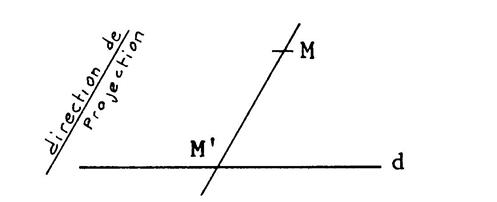
ci-dessous : la projection oblique  de « M »

Remarque 1 :

Dans le cas de projection orthogonale sur «  » , « M »  ayant pour image « M’ »,   « M’ » est appelé le projeté orthogonal de « M » sur «  ».

Remarque 2 :

Il arrive parfois que l’on dise « projection » sans préciser la direction de projection.

Il S’agit alors d’une projection orthogonale ( il en est de même pour  le projeté.

Fiche 3 : Cosinus de l’angle aigu de deux droites.

Info @ +++

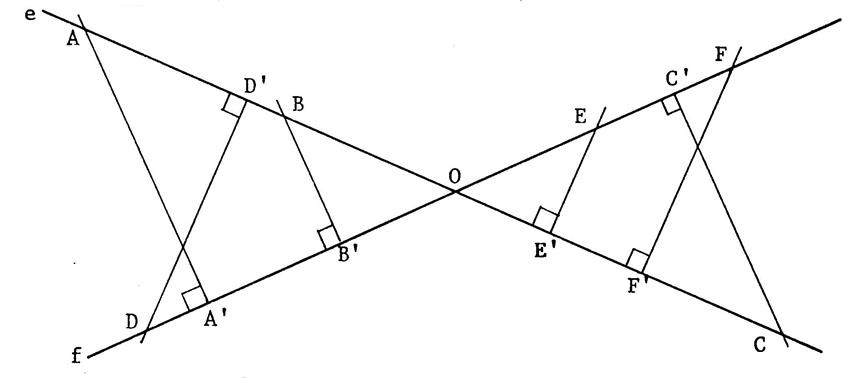
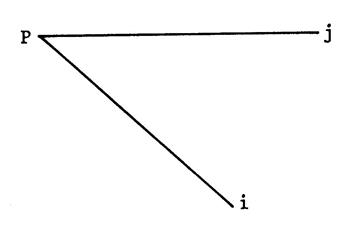
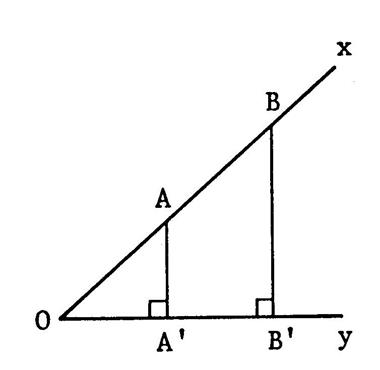
Ci-dessous on a tracé deux droites « e » et « f » se coupant en « O ».

On  a choisi des points quelconques sur « e » que l’on a projeté orthogonalement sur « f » et  des points quelconques  sur « f » que l’on a projeté sur « e ». .

Activité n° 2 :

Après avoir effectué les mesures nécessaires , déterminez approximativement l’opérateur de projection orthogonale de « e » sur « f » .  (prendre deux chiffres après la virgule )

Activité n° 3 :

De même déterminez l’opérateur de projection orthogonale de « f » sur « e » .  (prendre deux chiffres après la virgule )

Activité n° 4 :

Vous constatez que l’on trouve sensiblement le même nombre dans tous les cas.

Il est possible de faire une démonstration prouvant que :

       L’opérateur de projection orthogonale de « e »  sur « f » est le même que  l’opérateur de projection  orthogonale de « f » sur « e ».

Il en est ainsi pour toute paire de droite.

Ce nombre qui ne dépend pas des points choisis pour le déterminer , dépend uniquement de l’angle aigu des deux droites.

Définition :

On appelle « cosinus » de l’angle aigu de deux droites l’ opérateur  de projection orthogonale  de l’une sur l’autre.

Activité n° :

Mesurez l’angle aigu des droites « e » et « f ».  Vous trouvez ……°

Vous avez trouvé que le cosinus est sensiblement égal à «  0,67 ».

On écrit alors

( on lit « cosinus 48 ° »  )

Fiche 4 : Exercices .

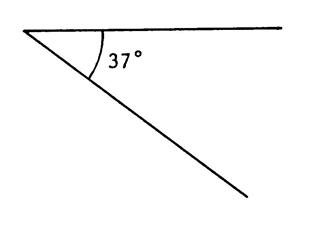
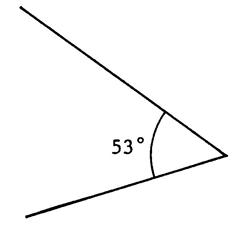
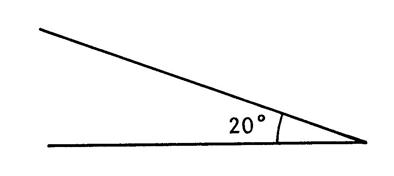
Exercice 1 .

 On vous donne le dessin de  3 angles tous égaux à « 42° ».

Après avoir choisi un point sur l’un des côtés de l’angle et l’ayant projeté orthogonalement sur l’autre côté  , détermine approximativement dans les trois cas , le cosinus de l’angle de « 42° ».

   = 

   = 

   = 

Trouvez-vous sensiblement le même nombre dans les trois cas ? ………………………………………

Etant donné un angle aigu , le cosinus de cet angle ne dépend pas du dessin le représentant .

Exercice 2 .

Après avoir fait les constructions nécessaires, déterminez approximativement le cosinus des angles représentés ci-dessous.

   = 

   = 

   = 

Exercice 3 .

On donne un  angle aigu   tel que  .

1°) Un point « A » de  «   »   se projette orthogonalement  sur « A ‘ » sur «   »   .

Sachant que « OA = 42 mm » , vous allez calculer  « OA’ ».

Vous savez que . , vous en déduisez que

D’où

2°)  Un point « B » de  «   »   se projette orthogonalement  sur « B ‘ » sur «   »   .

Sachant que « OB’ = 55 mm » , vous allez calculer  « OB ».

Vous savez que . , vous en déduisez que        ou    ;

D’où

Fiche 5 : Fabrication d’une table de cosinus.

Info  sur les tables de trigonométrie ++ @  

Nous allons vous expliquer ce que vous devez faire dans l’exercice suivant ;

On vous demande de remplir le tableau donnant le cosinus des angles de « 5° » en « 5° » de « 0° » à « 90° ».

Pour cela , utilisez le quart de cercle de rayon « 100 mm »qui y est dessiné.

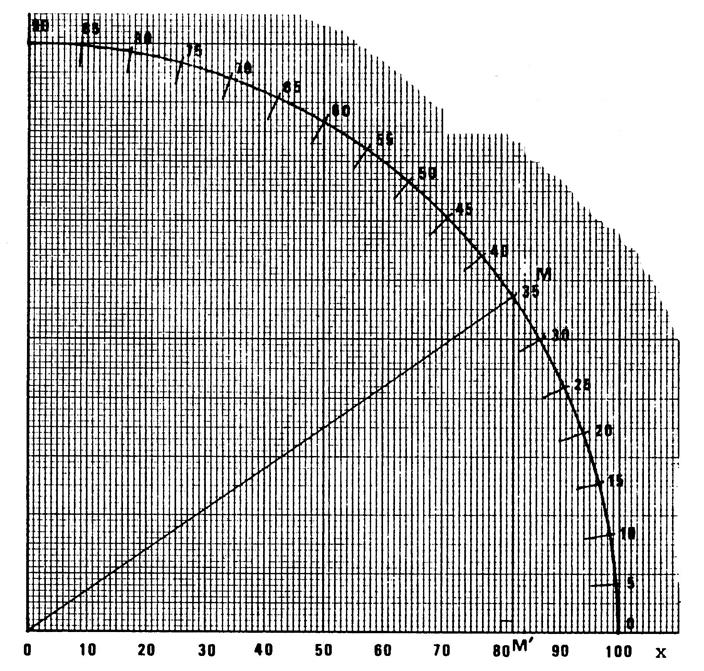
Exemple : considérons l’angle de « 35° » représenté sur le dessin par l’angle .

Le point « M » se projette orthogonalement  en « M’ » .  « OM = 100 mm », vous lisez « OM’ =  82  mm »

On a alors  « 

Faîtes de même pour tous les autres angles mais ne tracez rien sur la figure.

Angle

Cosinus.

0

5

10

15

20

25

30

35

0,82

40

45

50

55

60

65

70

75

80

85

90

Constatation :

Grâce à ce dessin, vous constatez que  «   et     , que tout angle aigu a un cosinus et un seul  et que ce cosinus est un nombre compris entre  « 0 »  et « 1 ».

Inversement , étant donné un nombre compris entre « 0 » et « 1 » , il lui correspond un angle aigu unique dont le cosinus est le nombre donné.

Fiche 6 : Représentation graphique …de la fonction « cos. » .

En utilisant ce qui précède , faites la représentation graphique de la fonction qui à tout angle aigu fait correspondre son cosinus.

Y-t-il proportionnalité entre le cosinus et l’angle ?

……voir cours …………………………………………………….

Grâce à ce graphique  déterminez par simple lecture :

Cos 32° = ……………………

Cos 67° = ……………………

Trouvez une valeur approchée des angles « x » et « y » tels que :

Fiche 7 : Dans le triangle rectangle.

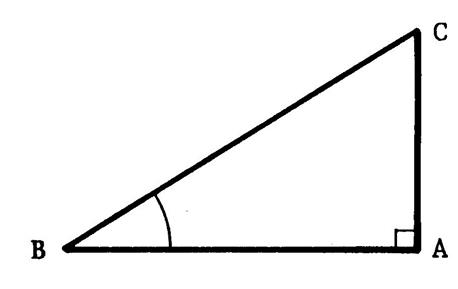
Ci-contre , un triangle rectangle en « A ».

En considérant que l’on projette orthogonalement la droite ( BC ) sur la droite ( BA ), on peut écrire.

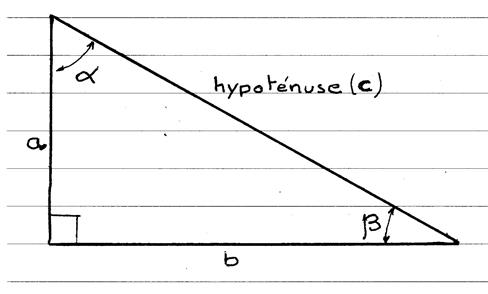
Vocabulaire :

Dans tout triangle , le côté opposé à l’angle droit s’appelle  « l’ hypoténuse ».

Dans le triangle « ABC », on dit que  [ BC ]  et  [ BA ] sont les côtés adjacents à l’angle .

Puisque  [ BC ]   est appelé l’hypoténuse , alors [ BA ] est appelé « côté adjacent à . ».

Avec ces notations , nous écrirons schématiquement :

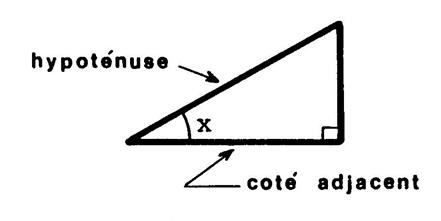
« x » désignant un angle aigu d’un triangle rectangle ; nous pouvons écrire la formule :

Remarque :

Dans la formule , quand on écrit  « côté adjacent » , on fait un abus de langage, on devrait écrire  « mesure de la longueur du côté adjacent » , ( on dirait de même pour l’hypoténuse : « mesure de la longueur de l’hypoténuse » ).

Exercice 1 :

Sur la figure ci-contre mesurez ( en mm)  « BA » et « BC » et calculez une valeur approchée à « 1° » près de  «  ».

Vous trouvez :

 «  BA = …. » ; «  BC = …. » ;  ;

En utilisant la table ou la représentation graphique (fiche 6) ou une calculatrice , donné la valeur approchée de «  ».

Vous trouvez «  ».

Mesurez «  ».

Vous trouvez «     ……………».

v Grâce à la formule encadrée ci-dessus , on peut écrire :

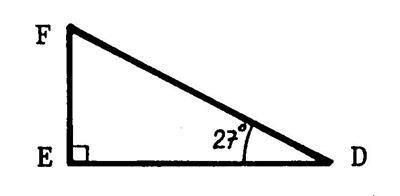
Exercice 2

« EDF » est un triangle rectangle  en « E »  tel que « FD = 50 mm » et  .

Vous allez calculer « ED » et « EF ».

Solution :

Calcul de « ED » :  On pose :  ;

Vous en déduisez  que

En utilisant la table ou la représentation graphique de la « fiche 5 »   ou une calculatrice  vous trouvez

Vous pouvez écrire  alors :    ,

Calcul de  : sachant que    vous en déduisez que 

     vous en déduisez que

   d’où   

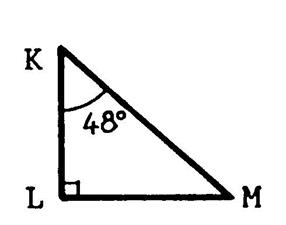
Exercice 3

« KML » est un triangle rectangle  en «L »  tel que « KL = 86 cm » et  .

Vous allez calculer « KM » et « LM » ( à 1 cm près ) .

Solution :

Calcul de KM :

 ,     vous en déduisez 

En utilisant la table ou la représentation graphique de la « fiche 5 »   ou une calculatrice  vous trouvez

Vous pouvez écrire  alors  que        =  128,53

Calcul de LM :

A vous de travailler : trouvez la valeur de  l’angle  «  90° - 48°  = 42° » ; cos 42° = 0,7431 ;  LM =  128,53  fois  0,7431 …

Fiche 8 : Construction d’un angle connaissant son cosinus.

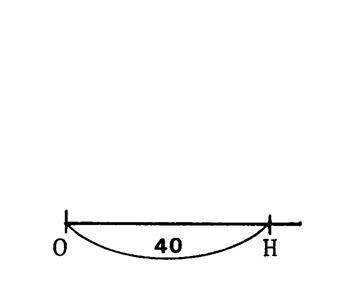
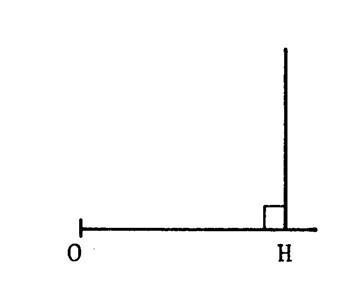
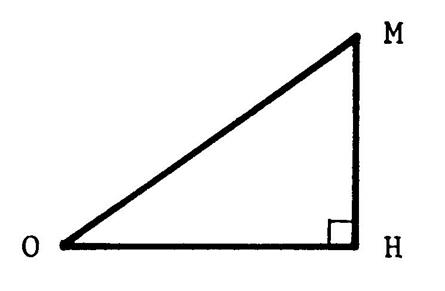
Construire un angle aigu   sachant que 

Tout revient à construire un triangle « OMH »  rectangle en « H » tel que   

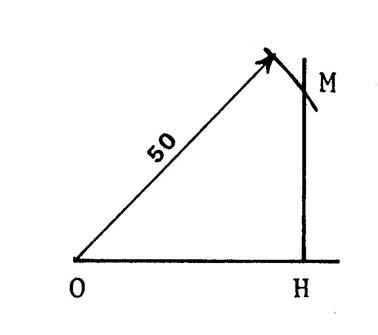
Et  

Choisissons par exemple  « OH = 40 mm »  et «  OM = 50 mm » 

Ci-dessous  nous vous donnons les étapes de construction :  

Etape  1

Etape  2

Etape  3

Etape  4

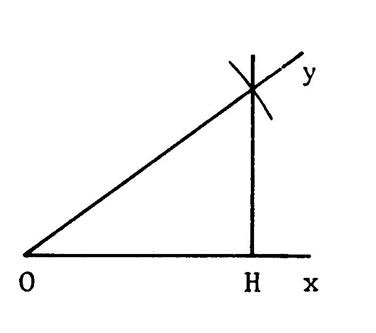
Refaites cette construction ci-contre

Construisez ci-contre  un angle aigu    tel que

Remarque :

Le problème est toujours possible à condition que le nombre donné pour le cosinus soit un nombre compris entre   « 0 » et « 1 ».

Fiche 9   Exercices .

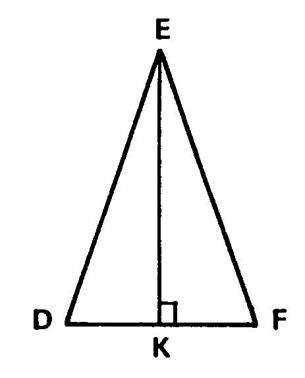
Exercice 1 :

« EFD » est un triangle isocèle de base  [ DF].

[ EK] est la hauteur . « EK = 50 mm »  , .

Calculez les côtés du triangle « EFD »  ( à 1 mm près).

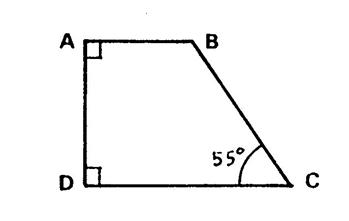
Exercice 2 :

« ABCD » est un trapèze rectangle en « A » et « D ».

« AB = 43 mm » , « BC = 80 mm »  .

Calculez l’aire de ce trapèze.

Exercice 3 :

« ACB » est un triangle tel que « AB = 120 mm », . ; .

Tracez la hauteur [ AH ].

Vous calculerez les longueurs à 1 mm près.

1°) Calculez   ;  ;

2°) Calculez  « AH » et « BH ».

3°° Calculez « AC » et « HC » puis « BC » .

Refaire les fiches ci-dessus !!!

TRAVAUX AUTO FORMATIFS :

CONTROLE :

1°)  Traduire en langage littéral :

« cos  a »    lire :   

« cos  b »  lire :

2°)   Traduire en symbole mathématique :

« cosinus de l’angle alpha »   : …………………………………..

 « cosinus de l’angle bêta » : ……………………………

3°)   Traduire en langage littéral :

cos a =

4°)  Traduire en langage mathématique

« Le cosinus d’un angle ; dans un triangle rectangle ;  est égal au rapport de la longueur du coté  adjacent  sur la longueur de l’hypoténuse. »

5°)  Compléter les phrases suivantes  : 

·       Le cosinus est un nombre qui n’a pas ................. ;Précisez ses limites  numériques en fonction des angles .........

·       Quand on connaît le cosinus d’un angle ...........................................

·       Quand on connaît la valeur d’un angle .........................................

6°) *Donnez la définition littérale d’un « cosinus ».

7°)   Donnez son modèle mathématique.

EVALUATION :

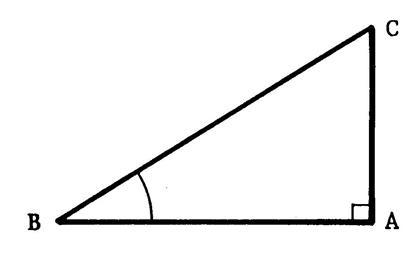
Compléter  les  tableaux suivants :

Avec la table :

Avec la calculatrice :

Au choix  (calculatrice ou table)

Soit un triangle rectangle : (Voir la figure  ci-dessus )

I  ) Compléter le tableau :      ( prendre   a  = 60° )

II  )  Compléter le tableau suivant :

   l’angle  a  = 60°

III) Compléter le tableau :

Au choix  (calculatrice ou table)

xd

Soit un triangle rectangle :

I  ) Compléter le tableau :      ( prendre   a  = 60° )

II  )  Compléter le tableau suivant :

   l’angle  a  = 60°

III) Compléter le tableau :