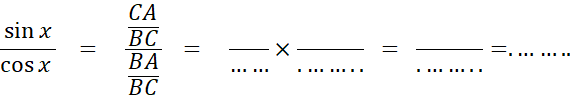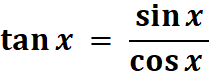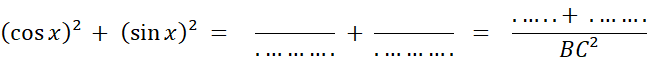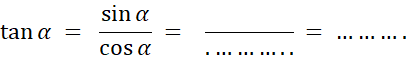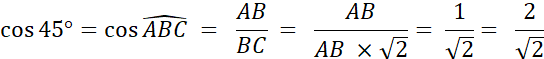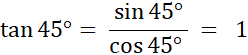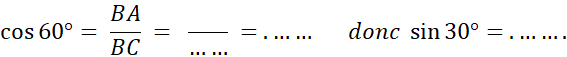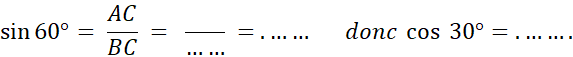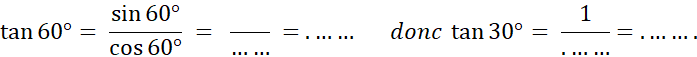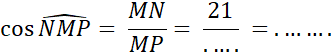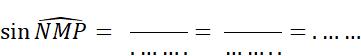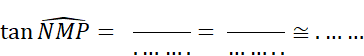|
|
|
|
Classe 3ème
collège |
|
|
|
|
|
|
|
|
|
|
|
|
fiches corrigées (reste à faire)… |
Pré requis :
|
Le système sexagésimal |
|
|
Le triangle rectangle |
|
|
Le produit en croix |
Environnement du dossier :
|
Objectif précédent : 3°)premières Fiches
sur la trigo 3ème |
Objectif suivant : |
info Présentation :
liste des cours disponible sur la trigonométrie |
|
|
|
|
|
|
La
trigonométrie au 3ème
collège :
(suite )
|
|
Fiche 4 :
Suite ( relations entre sinus, cosinus et tangente
d’un angle aigu) |
|
|
|
Fiche 5 : Angles complémentaires : |
|
|
|
Fiche 6 : Angles remarquables. |
|
|
|
Fiche 7 : Représentation graphique . |
|
|
|
Fiche 8 : Exercice dans le triangle
rectangle. |
|
|
|
Fiche 9 : Calculs dans le triangle
rectangle. |
|
|
|
Fiche 10 : Situations problèmes. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé évaluation |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 4 :
Suite ( relations entre sinus, cosinus et tangente
d’un angle aigu) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
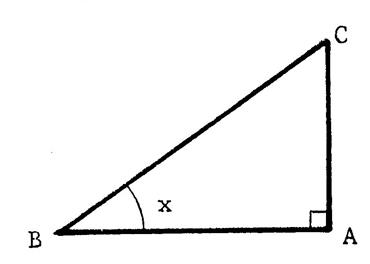
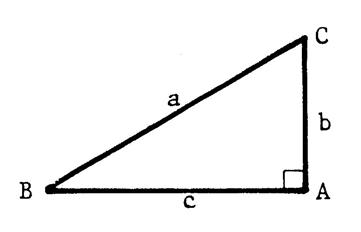
Reprenons le triangle « ABC3 de la fiche 2. Et
désignons par « x » l’angle Complétez :
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On dira alors : « x » désignant un
angle aigu quelconque |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Remarque : cette égalité n’a pas de sens
si « x = 90° » ( expliquez pourquoi ). Complétez :
Or, le triangle « ABC » est rectangle
en « A » , Donc , grâce au théorème de
Pythagore : Donc Au lieu de
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On dira alors « x » désignant un angle aigu quelconque |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 1 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez
Et vous contrôlerez en déterminant |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Puisque
Déterminez
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 2 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 3 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calculez
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 4 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 5 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« x » désignant un angle aigu quelconque , développez et simplifiez au maximum :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 6 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
«
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 5 : Angles complémentaires : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Considérons le triangle rectangle
« ABC » . Désignons par Complétez :
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vous
constatez que :
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Théorème : Si deux angles sont complémentaires alors : -
Le sinus de l’un est
égal au cosinus de l’autre . -
La tangente de l’un est
l’inverse de la tangente de l’autre. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité : complétez : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 6 : Angles remarquables. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Angle de 45° |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« ABC » est un triangle rectangle en
« A » tel que
Vous en déduisez que Donc « ABC » est isocèle : Donc AB
= AC [ BC ] peut être considéré comme la diagonale d’un carré. Donc :
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Et |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Angle de 60° |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« ABC » est un triangle rectangle en
« A » tel que
Vous en déduisez que Donc « ABC » peut être considéré comme un
demi-triangle équilatéral dont la hauteur est [ AC]. En appelant « a » la longueur BC , on a : AB = …a sin |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
60° a pour
complémentaire : 30° |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Complétez le tableau : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Angle |
0° |
30° |
45° |
60° |
90° |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
sinus |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
cosinus |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
tangente |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 7 : Représentation graphique : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
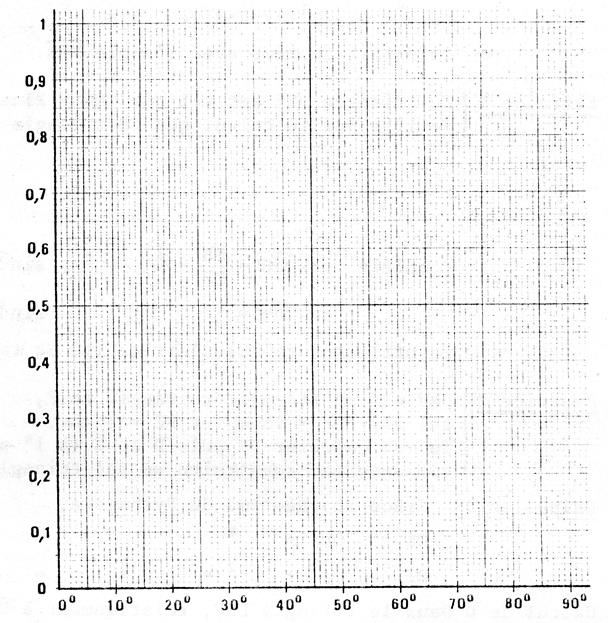
Vous allez faire la représentation graphique de
deux fonctions : -
La fonction qui à tout angle aigu fait
correspondre son cosinus. -
La fonction qui à tout angle aigu fait
correspondre son sinus. Vous ferez ces représentations sur le même
graphique mais avec des couleurs
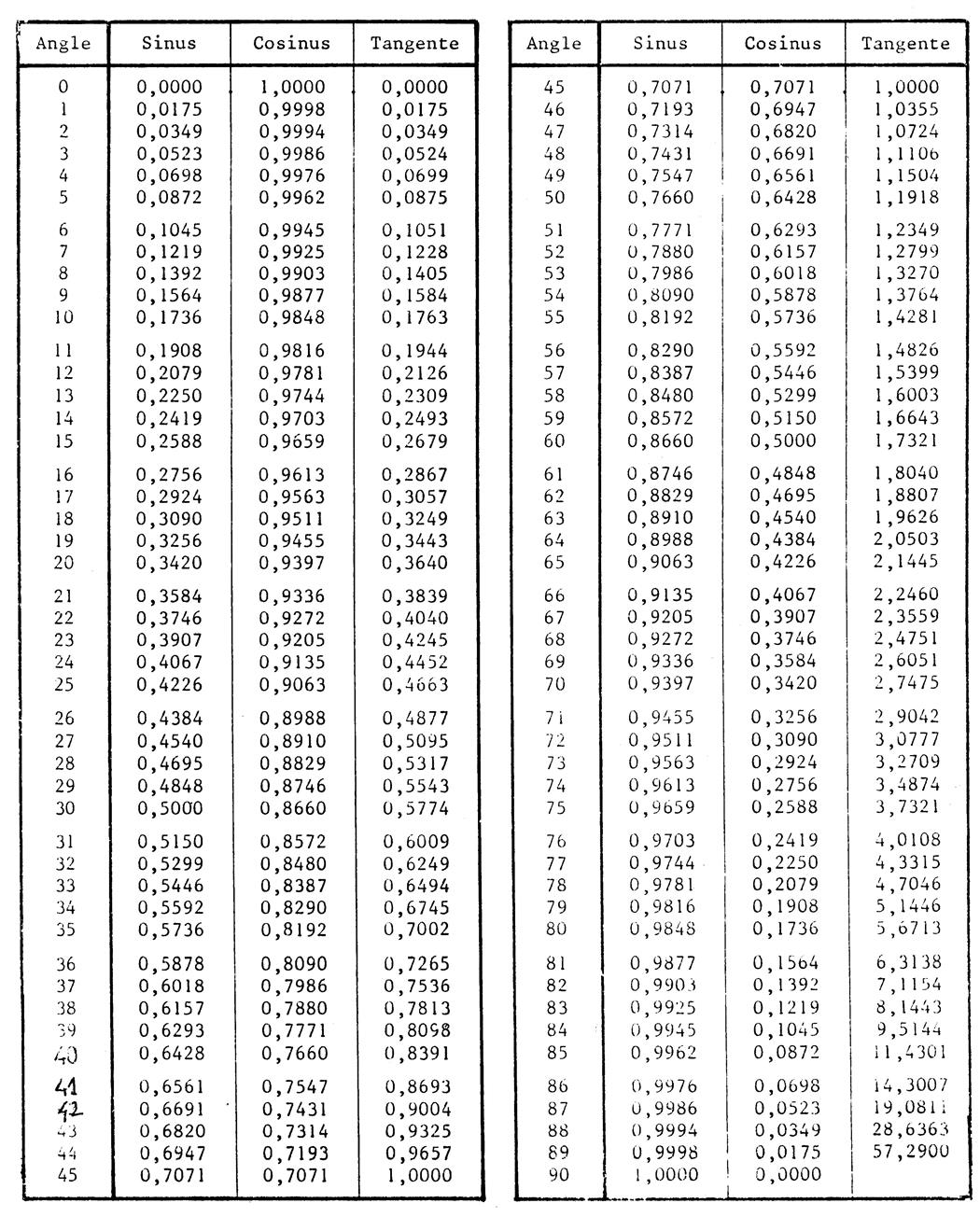
différentes. Auparavant, en utilisant votre calculatrice ou la
table de trigonométrie, remplissez le tableau donnant le cosinus et le sinus
des angles aigus de « 5° » en « 5° » (
2 chiffres après la virgule) et utilisez ce tableau pour faire vos
représentations graphiques. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Ces fonctions sont-elles des fonctions linéaires ?...... ( expliquez
pourquoi ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Y a-t-il proportionnalité entre le cosinus
et l’angle ou le sinus et l’angle ? |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Grâce à ces représentations graphiques , déterminez par simple lecture : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
cos 27° = |
cos 62° = |
sin 18° = |
sin 53°
= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· Trouvez une valeur approchée des angles « x » ,
« y » , « z » , « t » tel que : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 8 : Exercice dans le triangle
rectangle. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
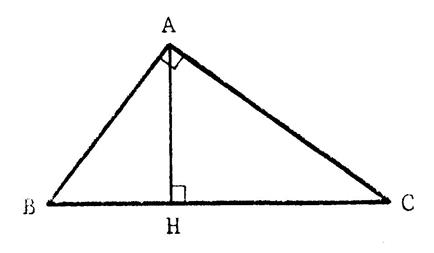
« ABC » est un triangle rectangle en
« A » . [ AH ]
est hauteur . 1°) En exprimant
Démontrons que : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dans le triangle rectangle « ABC » , Dans le triangle rectangle « ABH » , On peut donc écrire : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Rédigez les solutions des
question « 2 » et
« 3 » sur une autre
feuille. 2°) En exprimant
3°) Démontrez que : En calculant
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 9 : Calculs dans le triangle
rectangle. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
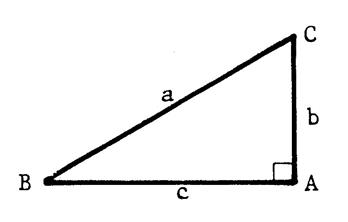
« ABC » est un triangle rectangle en
« A » . On désigne par Avec ces notations complétez : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
· On ferait de même avec l’angle |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 1 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
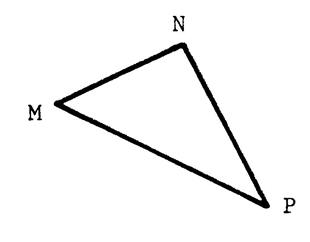
Le triangle « MNP » est tel que « MN = 21 mm »
, « NP= 28 mm » et « MP= 35 mm ». Vérifiez par le calcul que ce triangle est
rectangle en « N ». Complétez : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
En utilisant votre calculatrice ( ou la table
) , complétez : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 2 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« DEF » est un triangle rectangle en
« F », tel que « DF = 15 mm » et « FE = 36 mm ». On vous demande de calculer « DE » puis
Commencez par construire un tel triangle . a)
Calcul de
« DE » : Grâce au
théorème de Pythagore
, « DE² = DF² +
……² » ; DE² = . …..² + …….²
= ………..+ ……… = …………. ; DE
= ………. b)
Calcul de Dans le triangle « DEF » , relativement à « FE » représente le côté …………………… « DF » représente le côté …………………… Tu cherches parmi les formules de la « fiche
2 » celle qui fait intervenir ces
côtés. (il est préférable de choisir comme côtés ceux qui
sont donnés dans l’énoncé ). Vous trouvez : En utilisant votre calculatrice ( ou la table
) , vous trouvez c)
Calcul de « DEF » étant un triangle rectangle , |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 3 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« GHK » est un triangle rectangle en
« H ». Tel que
« GH = 16 mm » et « GK= 34 mm ». On vous demande de calculer « HK »
puis Commencez par construire un tel rectangle. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Calcul de « HK » : Grâce au théorème de Pythagore
, HK ² = …………- ………….. HK ² = …………- ………….. ; HK ² = …………- ………….. =
………….. ; HK Calcul de
En utilisant votre calculatrice ( ou la table
) , vous trouvez a)
Calcul de « GHK » étant un triangle rectangle , |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 4 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« LMN » est un triangle rectangle en
« M ». tel que « LM = 42 mm » et
« Vous allez calculer « MN » et
« LN ». Commencez par construire un tel triangle. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a)
Calcul de
« MN » . Vous connaissez « LM » et vous voulez
calculer « MN ». Dans le triangle « LMN », relativement
à « « MN » représente le côté
……………………………….. Vous cherchez parmi les formules de la
« fiche 2 » celle qui fait intervenir ces côtés .
Vous trouvez :
En utilisant votre calculatrice ( ou la table
) , vous trouvez On a alors « MN b)
Calcul de
« LN » . En procédant comme précédemment
, vous trouvez :
En utilisant votre calculatrice ( ou la table
) , vous trouvez On a alors « LN |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 5 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« PRS »
est un triangle rectangle en « R » tel que « PR = 28 mm » et On vous demande de calculer « PS » et
« RS ». Commencez par construire un tel triangle. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a)
Calcul de
« PS ». En procédant comme aux exercices précédents , vous trouvez :
En utilisant votre calculatrice ( ou la table
) , vous trouvez On a alors « PS b)
Calcul de
« RS ».
En utilisant votre calculatrice ( ou la table
) , vous trouvez On a alors « RS |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 6 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« TUV » est un triangle rectangle en
« U » tel que « TV = 54 mm » et « ON vous demande de calculer « TU » et
« UV ». Commencez par construire un tel triangle. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a)
Calcul de
« TU ».
En utilisant votre calculatrice ( ou la table
) , vous trouvez On a alors « TU b)
Calcul de
« UV ». |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Activité 7 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On donne un cercle de rayon « 6 cm ». [ AB ] est un diamètre, [ AC ] est une corde telle que « AC = 8 cm ». Calculez |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Fiche 10 : Situations problèmes. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 1 : « ABCD » est un rectangle de centre « O »
tel que « AB = 12 cm » et « BC = 3 cm ». Calculez |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 2 : |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
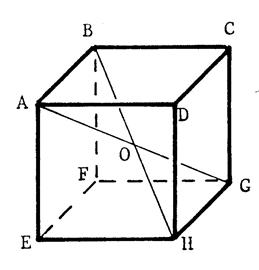
« ABCDEFGH » est un cube de 10 cm
d’arête. 1°) Calculez l’angle 2°)
« O » étant le point d’intersection des diagonales [ AG ] et [ BH] , calculez |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
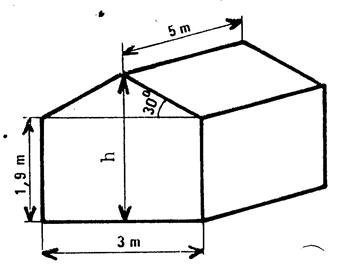
D’après le brevet Grenoble (
1988) , on veut construire un garage dont les dimensions sont données
sur le dessin ci-contre. 1°) Calculez la hauteur « h » du
garage. On donnera une valeur affichée à 1 cm près. 2°) Calculez l’aire « S » du toit . On donnera une valeur approchée par excès à 1 dm²
près. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« SRT » est un triangle rectangle en
« R ». [ RJ ] est hauteur , « RJ = 6 mm » , « SJ = 4 mm ». Calculez « SR » , « ST » ,
« JT » , « RT ». Donnez les valeurs exactes. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 5 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
D’après un brevet 1987 . « ABC » est un triangle rectangle d’ hypoténuse [ BC
]. Une parallèle à ( BC)
coupe [ AB ] en « E » et [
AC ] en « F ». On pose « AE = x » . 1°) Sachant que « AB = 10 cm » et
« AC = 7,5 cm » , calculez BC. 2°) Comparez les angles : En évaluant
3°) « H » et « G » sont les
projetées orthogonaux respectifs de « E » et « F » sur (BC ). Evaluez de deux façons différentes En déduire
une relation entre « EH » et « x ». 4°) A quelle condition simple le quadrilatère
« EFGH » est-il un carré ? Déterminez « x » pour que « EFGH » soit un carré. On donnera d’abord la valeur exacte de
« x » , puis la valeur approchée à 0,01 mm
près par excès.. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 6 . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« ABC » est un triangle rectangle en « A » .
La bissectrice de Sachant que « BA = 85 mm » et |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 7 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« EDF » est un triangle tel que Calculez |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 8 . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On considère un cercle de centre « O »
dont le rayon est 24 cm. « M » est un point tel que « OM = 63 cm ». On trace
par « M » deux tangentes au
cercle. On désigne par « E » et « F »
les points communs au cercle et à ces tangentes. Calculez une valeur approchée (
à 1° près ) de l’angle |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 9 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« ABC » est un triangle rectangle en « A » tel que [AM] est
médiane [ AH]
est hauteur. 1°) Démontrez que le triangle « BMA »
et « CMA » sont isocèles. 2°) Donnez la valeur en degré de 3°) Sachant que « BC = 20 cm » , calculez « AM » , « MH » ,
« HA » , « HC » , « AC ». 4°) Déterminez la valeur exacte de ( pour cela , calculez le sinus de |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Problème 10 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
« ABC » est un triangle isocèle tel que
« AB = AC = a » , [ AH] et [ BK]
sont deux hauteurs. 1°) On
désigne 2°) En utilisant « a » et « 3°) En
utilisant « a » et l’angle «
2 4°) Déterminez une égalité entre |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||