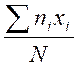Nota :  les cours proposés n’ont pas pour objectif  de vous apprendre  à utiliser une  calculatrice .

 Pour utiliser la calculatrice , il faut utiliser le livret fourni (chaque marque à son livret ) . Dons tous les cas on ne peut bien utiliser la calculatrice que  si on comprend ce que va calculer cette calculatrice .    

 Pré requis:

 

Les Statistiques  info
Voir : les conventions d’écriture en algèbre
Voir : la signification des principaux symboles  d’écriture en algèbre.

 

ENVIRONNEMENT du dossier:

Index  warmaths

Objectif précédent   1°) les enquêtes et observations .

Objectif suivant 1°) les caractéristiques de tendance centrale et de position. 2°) les caractéristiques de dispersion.

Info géné. 2°) liste des objectifs 3°) voir : médiane graphique avec les ECC et les ECD…

 

	DOSSIER : Résumé  des observations des données statistiques: Définitions : Les indices ( dit aussi : indicateurs) de position et de dispersion
	-      A  ) Les indicateurs de position :    1°)  les quatre indicateurs (indices) de position :  (mode ; médiane ; quartile ; les moyennes dont la moyenne :        )   2°) Comparaison de la médiane et de la moyenne d’une même série.   -      B )  les quatre indicateurs ( indices) de dispersion. ( l’étendue ; l’intervalle interquartile ; la variance ; l’écart type.)

 

 

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

Info. COURS

 

Résumé  des observations :

 

Les observations recueillies nous permettent de repérer deux catégories d’indices (ou indicateurs) qui vont nous permettre de décrire un ensemble ou des ensembles de données. (nous nous situons par rapport aux données de score  (nombres)  :

Ces indices sont des indices de position  ( mode ; médiane ; moyenne et quartile )  et des indices de dispersion. ( étendue ; l ’intervalle interquartile ;  variance et écart type  )

 

Attention : Ne pas confondre avec les indices de la vie économique. ( info ++++)

 

 

 

 

 

A ) Les « 4 »  indices  (indicateurs)  de position :

 

1°)    Ces indicateurs    : « mode » ; « médiane » ; « quartiles » , « moyenne »  vont mettre en valeur  certaines  caractéristiques de la variable.

 

1)    Le mode :

 

                Le mode est la valeur de la variable pour laquelle est observée la plus grande fréquence.

 

2) La médiane :

 

  La médiane permet de trouver la valeur de la variable telle qu’il y ait autant de mesures qui lui soient inférieures que de mesures qui lui soient supérieures.

Identification du rang médian :

 

Exemple : si nous reprenons le tableau des mesures de tailles

, si nous opérons le cumul des effectifs , nous constatons que le 15^ème événement se situe parmi les 3 événements : 1,75 m. La médiane est égale à 175

 

Taille inférieure ou égale à	162	167	172	177	182	187	192
Nombre d’observations cumulées	2	6	11	20	26	29	30

 

La médiane appartient à l’intervalle médian [173-177[

Nous verrons que l’on peut obtenir la valeur  de la médiane en traçant la ligne polygone des ECC et des ECD.  ( détermination du point médian)

 

 

3) les quartiles.

 

 

4) les moyennes .

 

 

4-1         ) La moyenne :                       application : moyenne arithmétique pondérée par les effectifs

=

 

4- 2 ) Comparaison de la médiane et de la moyenne d’une même série.

 

On retiendra :   le calcul de la médiane consiste à partager  la population en deux parties égales  alors que le calcul de  la moyenne

 

Exemple L à venir )

 

 

 

 

B) les  « 4 »  indices (dit aussi : paramètres ) de dispersion :

 

Ces indices  ( paramètres)  ( étendue ;l ’intervalle interquartile , la  variance et écart type  )  rendent compte de l’étendue de la variation.

 

1°) Etendue : l’étendue est la différence entre la plus grande et la plus petite valeur du caractère .

 

2°) l ’intervalle interquartile

 

 

3°) La variance :

 

Exemple : considérons la notation par 2 professeurs qui ont la même moyenne mais des notes extrêmement différentes : l’un note de 2 à 18  , alors que l’autre note de 8 à 14 . Il se peut que le calcul de la moyenne des notes de chacun d’eux soit la même. Il faut un autre indicateur.

 

Cet indicateur sera la « somme des carrés des écarts » , que l’on appellera « variance ».

 

Un écart est égal à la différence d’une note d’un élève avec la note moyenne (calculée) .

 

4°) Ecart  type : l’écart type est la racine carrée de la variance .

 

 

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

1°)  Citer les indices (indicateurs) de position . ( précisez)

 

2°) Citer les indices (indicateurs)   de dispersion. ( précisez )

 

EVALUATION

INTERDISCIPLINARITE

corrigé CONTROLE :

 

Qu’est qu’un « indice »  ?

L’indice : l’indice est un nombre (supérieur à 0 ) qui a pour but de traduire de l’évolution dans le temps d’une grandeur mesurable :

 

corrigé EVALUATION

 

corrigé INTERDISCIPLINARITE