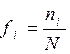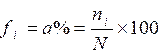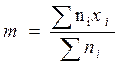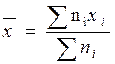|
|
|
|
N°13 |
LES Caractéristiques d’une série
statistique : RESUME : VOCABULAIRE et
LES CALCULS DE BASE en STATISTIQUE |
|
Rappel
|
|
||||||||||||||||||||||||||||
|
|
Lorsque
la variable étudiée (
les xi ) peut prendre différentes valeurs . Si elles
sont nombreuses elles sont réparties en classes. |
||||||||||||||||||||||||||||
|
|
Nous
savons que l’amplitude d’une classe est la différence entre la valeur
maximale et la valeur minimale de la classe. |
||||||||||||||||||||||||||||
|
|
L’effectif
d’une classe (notée : f i ) est le nombre de cas où la valeur de la
variable est comprise dans la classe . ( voir le segment semi ouvert tel que la borne « a » est
incluse et « b » est exclue) |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
1
- |
Fréquence : On
appelle « fréquence d’une classe »
(noté fi
) : le rapport entre
l’effectif de la classe ( noté :
ni ) et l’effectif total. (
noté : N) |
||||||||||||||||||||||||||||
|
Question
1 |
Qu’appelle
–t-on fréquence ? |
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
Info. cours : la fréquence peut être
exprimée par 2 valeurs : sous la forme d’un nombre
décimal (inférieur à 1) et ou sous la forme d’un « pourcentage » |
||||||||||||||||||||||||||||
|
|
cas 1 : |
Cas
2 = |
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
2
_ |
Effectifs
Cumulés Croissants |
|
|||||||||||||||||||||||||||
|
|
L’effectif
cumulé croissant de la première classe est égal à son effectif . |
Exemple :
|
|||||||||||||||||||||||||||
|
Question
2 |
Traduire : E. C.C. |
Classe
|
effectif |
ECC |
|||||||||||||||||||||||||
|
Question 3 |
A
quoi est égal L’ECC d’une classe ? |
Cl
1 |
7 |
7 |
|||||||||||||||||||||||||
|
|
L’ ECC d’une
classe est égal à L’ ECC de la classe
précédente plus l’effectif de la classe. |
Cl
2 |
17 |
(17+7) 24 |
|||||||||||||||||||||||||
|
|
Remarque 1 : L’
ECC de la dernière classe est égal à l’effectif total. |
Cl
3 |
34 |
(24+34) 58 |
|||||||||||||||||||||||||
|
|
Remarque
2 : L’ ECC de la classe [a ;
b [ (segment semi ouvert) est le nombre de cas où la variable est
inférieur à « b » . |
Cl
4 |
12 |
70 |
|||||||||||||||||||||||||
|
|
|
|
70
|
(= 70) |
|||||||||||||||||||||||||
|
3
_ |
Effectifs
Cumulés Décroissants |
Exemple :
|
|||||||||||||||||||||||||||
|
Question
4 |
A
quoi est égal le ECD de la première
classe |
Classe
|
Effectif
|
E
D C |
|||||||||||||||||||||||||
|
|
Le E.C.D
de la première classe est égale à l’ effectif total . |
Cl
1 |
7 |
70 |
|||||||||||||||||||||||||
|
|
Remarque
1 : l’ E.C.D. d’une classe est
égal à l’effectif cumulé décroissant de la classe précédente moins l’effectif de la classe. |
Cl
2 |
17 |
(70
– 17) = 53 |
|||||||||||||||||||||||||
|
|
L’
E.C.D. de la dernière classe est égal
à son effectif. |
C
l 3 |
34 |
(53
– 34) = 19 |
|||||||||||||||||||||||||
|
|
L’E.C.D. de la classe [ a ; b [ est le nombre
de cas où la variable est supérieure à « a ». |
C
l4 |
12 |
(19-12)
= 7 |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
4
_ |
Exemples
|
||||||||||||||||||||||||||||
|
Question
5 |
a)
Série discontinue |
||||||||||||||||||||||||||||
|
|
Dans
une série discontinue , le mode est la valeur dont l’effectif est le plus
élevé. |
xi |
ni |
|
|||||||||||||||||||||||||
|
|
Dans
une série continue , la classe modale est la classe dont l’effectif est le
plus élevé. |
X1 |
12 |
|
|||||||||||||||||||||||||
|
|
|
X2 |
36 |
|
|||||||||||||||||||||||||
|
|
|
X3 |
47 |
Mode |
|||||||||||||||||||||||||
|
|
|
X4 |
23 |
|
|||||||||||||||||||||||||
|
|
|
b)
Série continue : |
|||||||||||||||||||||||||||
|
|
|
Classe
|
ni |
|
|||||||||||||||||||||||||
|
|
|
Cl
1 |
4 |
|
|||||||||||||||||||||||||
|
|
|
Cl2 |
17 |
|
|||||||||||||||||||||||||
|
|
|
Cl
3 |
36 |
Classe
modale |
|||||||||||||||||||||||||
|
|
|
Cl
4 |
23 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
Ce
calcul concerne le calcul de la moyenne des valeurs pondérées par les
effectifs. |
|
|||||||||||||||||||||||||||
|
|
Dans
une série continue (constitution de classe )
,il faut d’abord calculer le centre de chaque classe : « xi » |
Classe
|
Effectif
« ni » |
Centre
de classe « xi » |
Calculs
des produits: « ni
xi » |
||||||||||||||||||||||||
|
|
Nous
désignons par « ni » l’effectif de chaque classe. |
[0 ; 10 [ |
8 |
|
|
||||||||||||||||||||||||
|
|
Procédure
de calcul (étapes) : |
[10 ; 20 [ |
9 |
|
|
||||||||||||||||||||||||
|
|
1°)
Compléter la colonne des centres de classe : « xi » |
[20 ; 30 [ |
16 |
|
|
||||||||||||||||||||||||
|
|
2°)
Calculer le produit « ni
xi » de chaque classe. |
[30 ; 40 [ |
9 |
|
|
||||||||||||||||||||||||
|
|
3°)
Calculer la somme des calculs des « ni xi » ;
que l’on note en mathématique : |
[40 ; 50 [ |
8 |
|
|
||||||||||||||||||||||||
|
|
4°)
Calculer le quotient « m » : |
Total ( |
50 |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Calcul de la
moyenne : |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
La
médiane est la valeur du caractère (de la
variable) tel que la moitié de l’effectif ait une valeur inférieure ou
égale. |
||||||||||||||||||||||||||||
|
|
|
Classe |
Effectif
« ni » |
ECC |
|
||||||||||||||||||||||||
|
|
On peut la
déterminer à partir de la Courbe des Effectifs Cumulés croissants. |
[0 ; 10 [ |
8 |
8 |
|
||||||||||||||||||||||||
|
|
|
[10 ; 20 [ |
9 |
17 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
[20 ; 30 [ |
16 |
33 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
[30 ; 40 [ |
9 |
42 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
[40 ; 50 [ |
8 |
50 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
Total ( |
50 |
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
1°) Détermination des coordonnées des
points.(permettant de tracer les segments…) |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
Point O |
|
|
Point A |
|
|
|
||||||||||||||||||||||
|
Abscisse
|
0 |
Valeur de début Classe de la [0 ; 10 [ |
|
10 |
Valeur de Fin
de Classe de la [0 ; 10 [ |
|
|
||||||||||||||||||||||
|
Ordonnée
|
0 |
Effectif de départ |
|
8 |
Effectif
correspondant à la limite supérieure de la classe [0 ; 10 [ |
|
|
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
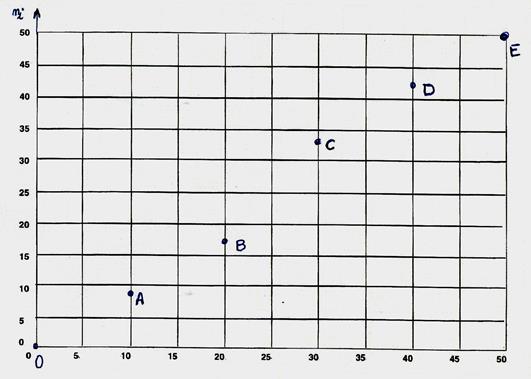
Et
ainsi de suite : Point
B : ( 20 ; 17 )
; Point C ( 30 ;
33) ; Point D ( 40 ; 42) ; Point E ( 50 ;50) |
||||||||||||||||||||||||||||
|
|
2°)
Représenter les sur le graphique (voir
ci dessous) |
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
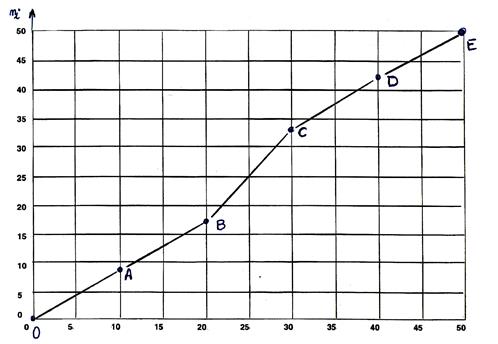
3°) et joindre ces points. Nous obtenons la
courbe des effectifs cumulés croissant. |
||||||||||||||||||||||||||||
|
|
Cliquez
sur l’image pour agrandir… |
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
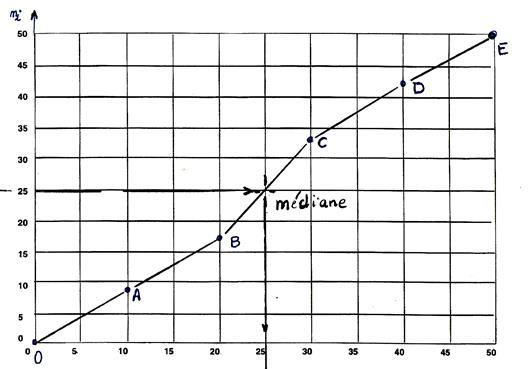
4°) Tracer une droite
« horizontale » dont le départ est égale à la moitié de l’effectif
( ici : 25.) C’est
une droite parallèle à l’axe des
abscisses ( dit aussi droite y= 25) |
la
moitié de l’effectif est aussi
appelé : effectif médian. L’effectif
médian correspond à 50% de l’effectif total est il
de calcul : |
|||||||||||||||||||||||||||
|
|
L’intersection
de cette droite et la courbe des E.C.C
donne un point qui permet de lire la valeur telle que la moitié de
l’effectif a une valeur inférieure ou égale. C’est la « médiane » |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
Remarque :
le point d’intersection des deux
courbes polygone des effectifs cumulés croissante et polygones des effectifs décroissants
définit les coordonnées du point médian de la série statistique étudiée. |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
L’Ecart
moyen arithmétique . |
|||||||||||||||||||||||||||||
|
|
Procédure
(étapes de calculs) |
|
|||||||||||||||||||||||||||
|
|
1°)
Calculer la moyenne de la série statistique. |
|
|||||||||||||||||||||||||||
|
|
Pour
chaque valeur de la variable (valeur du caractère) ,on calcule la valeur
absolue de l’écart par rapport à la moyenne.
|
|
|||||||||||||||||||||||||||
|
|
2°)Calculer les
distances : |
|
|||||||||||||||||||||||||||
|
|
3°)
Multiplier chaque distance ;par l’effectif correspondant : |
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
4°)
Faire la somme des différents produits obtenus . |
|
|||||||||||||||||||||||||||
|
|
5°)
Effectuer le quotient (diviser)
de la somme obtenue par l’effectif
total . ( N ) ; que l’on note aussi |
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||