Pré requis:

Les Statistiques info
Voir les fiches sur le lien entre les moyennes et la médiane ( collège classe de troisième)
ENVIRONNEMENT du dossier:
Warmaths		Objectif précédent : - vocabulaire et définitions -fréquence et effectifs Les indice de positions				Objectif suivant : Complément de cours sur la médiane s			Retour sur les cours de statistique
DOSSIER : La MEDIANE
TEST	COURS		Devoir Contrôle	Devoir évaluation	Interdisciplinarité			Corrigé Contrôle		Corrigé évaluation

La médiane partage l’effectif en deux parties égales : Cette valeur se détermine soit par calcul soit par graphique. On distinguera le cas de la variable discontinue (« bâtons »)de la variable continue (histogramme) : Pour la variable discontinue on ne trouvera pas de valeur médiane (sauf exception) donc « la médiane » sera recherchée dans le cas de série à variables continues.

COURS

1°) La médiane ( en abrégé « M » ou « Me ») est la valeur de la variable ( caractère) qui partage l’effectif total en deux parties égales, les éléments de la population étant rangés par ordre croissant ou décroissant. En d’autres termes , la médiane est la valeur statistique qui correspond , sur la courbe cumulative , à une ordonnée représentant une fréquence relative de 0,5 ou 50% , ce qui entraîne que 50% des observations seront inférieures à la médiane et 50% supérieures à celle - ci . . Remarque : la médiane a la même unité que le caractère. (on dit aussi : que La médiane est une grandeur )

Info : La valeur de la médiane peut se déterminer, soit par calcul numérique , soit graphiquement.

2°) Détermination de la valeur de la médiane par le calcul.

On distinguera deux cas : la variable est continue (dit aussi : caractère quantitatif continu) ou la variable est discontinue ( dit aussi : caractère quantitatif discret)

A ) Détermination de la médiane dans une série statistique ,dans le cas d’une variable continue : (organisation des données par classes)

Par définition : la classe à laquelle appartient la médiane est appelée : « classe médiane ». Exemple :

Valeurs

2 ; 3 ;5 ;7 ;7 ;9 ;

11 ;15 ;15 ;17 ;19

20 ;23 ;25 ;27

Classe

[ 0 ; 10 [

[ 10 ; 20 [

[ 20 ;30 [

Effectif : N = 14

6

5

4

La médiane de la série est

La classe médiane est donc [ 10 ; 20 [ ; 13 appartenant à cet intervalle.

Calcul numérique : L’équation de droite représentant la médiane est de la forme : y ( M) = 0,5 admet la solution dépendante de l’effectif étudié. Procédure : ■ Partager le total de l’effectif en deux : ( 2 possibilités) - Si le total des effectifs est « impair » : ( 2 n + 1) , le rang de la médiane est égal à : - Si le total des effectifs est « pair » ( 2n), les deux termes médians occupent « respectivement » les rangs : ■ Rechercher la classe correspondante au(x) rang(s) précédemment déterminé(s). ■ Déterminer, en postulant une répartition homogène des valeurs dans la classe, la valeur de la médiane par interpolation linéaire.

Application . Exemple : soit le tableau ci -dessous On veut : 1°) Evaluer le rang de la médiane 2°) Rechercher la classe correspondante au rang trouvé 3°) Trouver la valeur exacte de la médiane.

x i

Effectifs ( n i )

Simples

Cumulées Croissantes

Cumulées décroissantes

] 1000 - 1500 ]

6

6

65

] 1500 - 2000 ]

12

18

59

] 2000 - 2500 ]

25

43

47

] 2 500 - 3000]

17

60

22

] 3000 - 3500 ]

5

65

5

65

- Recherche du rang de la médiane : On remarque que l’effectif est impaire d’où l’évaluation du rang de la médiane :

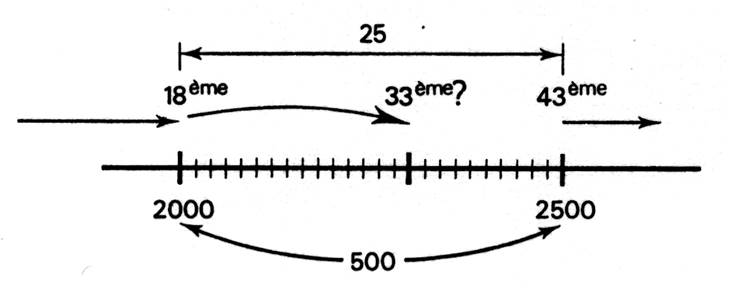
- recherche de la classe corresponde au 33^ème rang : Nous savons, d’après le tableau , que la valeur « 2000 » correspond au 18^ème rang et que la valeur « 2 000 » correspond au 43^ème rang. La valeur du 33^ème rang se trouve donc comprise entre 1500 à 2000 . La classe médiane est donc bien 1500 à 2000 . Pour trouver la valeur exacte , on doit procéder à une interpolation linéaire , comme indiquer par le schéma ci-dessus.

Calcul de la valeur exacte de la médiane : La valeur est obtenue en appliquant une simple règle de trois. Soit la médiane égale à « 2000 + ( ?= x)  » Calcul de la valeur « x » : On remarque que sur l’intervalle 2000 à 2500 , il y a un effectif de 25 On calcule la valeur de cet intervalle et 2500 - 2000 = 500 On divise cette valeur « 500 » pour la répartir pour à chaque élément de l’effectif : 500 / 25 = 20 ( valeur de 1 sous intervalle de la classe 2000 à 2500) 1 élément de la classe 2000 à 2500 « vaut » 20 ; pour arriver au rang « 33 » il faut connaître le nombre de sous intervalle qui part du rang « 18 » au rang « 33 » soit 33 - 18 soit = 15 ; il y donc 15 sous intervalles valant « 20 » soit 15 fois 20 = 300 aussi x = 300 Conclusion :la valeur de la médiane est égale à 2000 + 300 = 2300

2°) Détermination par le graphique :

A partir d’une fonction de répartition (voir les FFC) , la valeur de la médiane peut s’obtenir de deux façons :

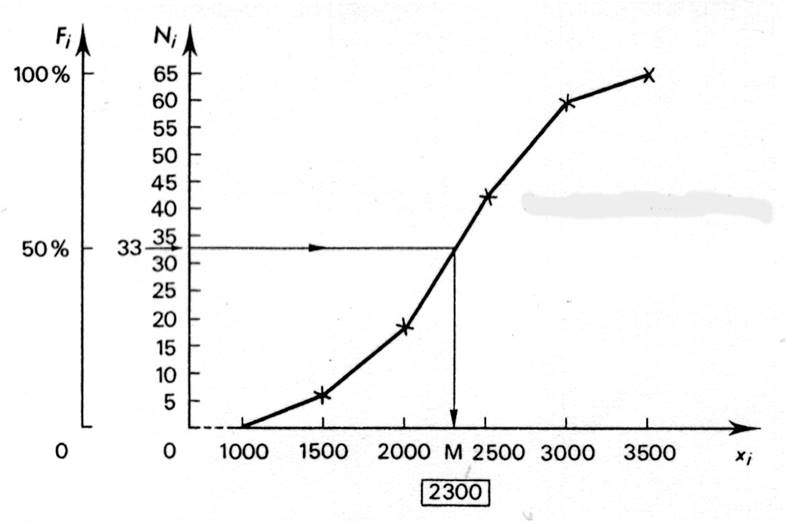
1 - Soit en traçant une parallèle à l’axe des abscisses au point d’ordonnées 50%. De l’intersection de cette droite avec la courbe de répartition , on abaisse une perpendiculaire qui indique sur l’axe des abscisses la valeur de la médiane. Exemple :à partir du tableau ci dessus ; on a tracée la courbe de la fonction de « Répartition » ;

remarquez : à 50% correspond le rang « 33 » qui fait correspondre la valeur de la médiane « 2300 ».

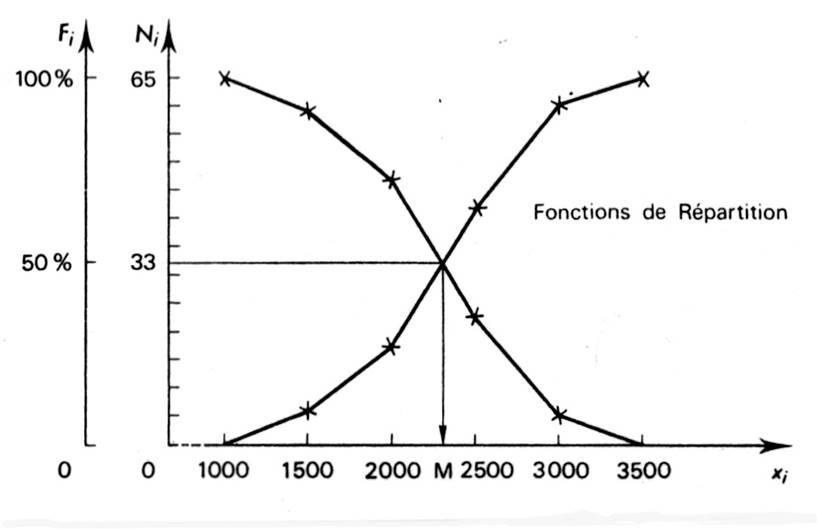
2 - On peut aussi obtenir la valeur de la médiane en traçant sur le même graphique les deux courbes des effectifs ou des fréquences cumulées croissantes et décroissantes. Le point d’intersection a pour ordonnée Fi = 50 % et pour abscisse la valeur de la médiane.

B ) Dans le cas d’une variable discontinue : ( dit aussi : caractère quantitatif discret)

Info : on rencontrera 2 cas, celui où les termes sont « impairs » ou « pairs ».

Cas 1 : la série discontinue possède un nombre de termes impairs et ces termes doivent être connus individuellement .

Exemple :la série discontinue possède 9 termes :

(On nous donne la série suivante) : 4 ; 6 ; 8 ; 10 ;12 ;13 ;15 ;16 ;20 . On remarque : - que les valeurs sont rangés par ordre croissant. -que le nombre de valeurs est impair ( 9 valeurs)

4

6

8

10

12

13

15

16

20

4 termes

Médiane

4 termes

La médiane de cette série de 9 nombres rangés par ordre croissant est « 12 ».

En conclusion : Si l’effectif total est impaire , la médiane est la valeur de la variable (caractère) située au milieu de la série.

Cas 2 : La série discontinue possède un nombre de termes pairs et ces termes doivent être connus individuellement .

Exemple :la série discontinue possède 8 termes : (On nous donne la série suivante) : 6 ; 8 ; 10 ;12 ;13 ;15 ;16 ;20 .

6

8

10

12

13

15

16

20

4 valeurs

Médiane 12,5

4 valeurs

La médiane de cette série de 8 nombres rangés par ordre croissant est

Détermination de la médiane par le graphique :

A partir d’une fonction de répartition :

3°) Propriétés .

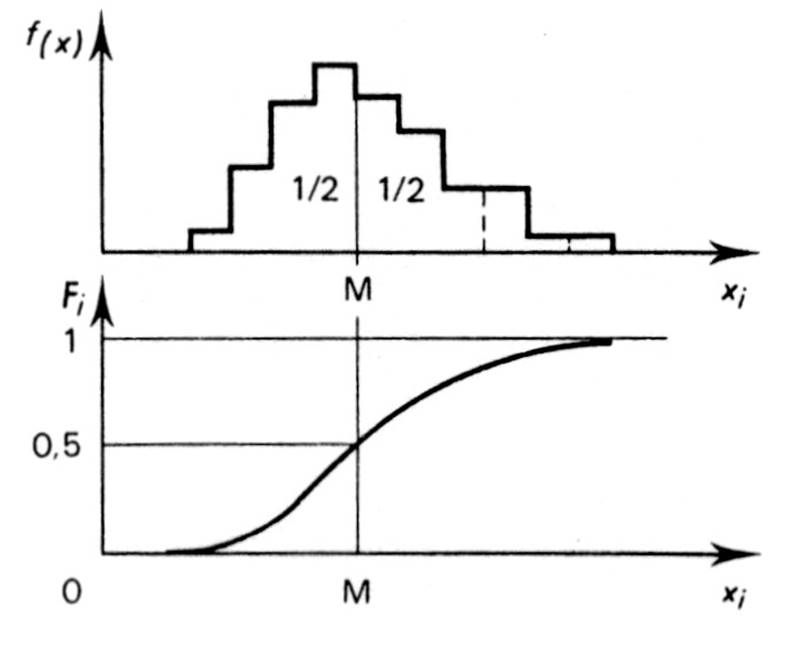
La médiane partage l’histogramme en deux aires égales à 1/2 . Elle dépend plus du rang des unités statistiques observées que des valeurs de la variable, et se trouve peu affectée par les variations des termes extrêmes. Ce que vous pouvez observer sur les deux représentations graphiques complémentaires.

COMPLEMENT :

Ce compléments a pour but de vous montrer comment on peut calculer la va leur de la médiane.

Rappel La médiane d'une série statistique est la valeur de la variable telle que le nombre de valeurs qui lui sont inférieurs est égal au nombre de valeurs qui lui sont supérieurs.

Graphiquement on peut déterminer sa valeur à l'aide du graphique des effectifs cumulés croissants et décroissants : La médiane est alors la valeur de l'abscisse du point d'intersection de ces deux courbes.

Prenons un exemple : Une distribution statistique a été établie après un contrôle radar sur autoroute, on a classé les données ( regroupées en classes) dans le tableau suivant :

Vitesse ( km/h)	Nombre de véhicules
[80 ; 100 [ [100 ; 120 [ [120 ; 130 [ [130 ; 140 [ (140 ; 150 [ [150 ; 170 [ [170 ; 190 [	120 90 100 120 40 20 10
Total	500

Si on complète ce tableau à l'aide des ECD et ECC :

Vitesse ( km/h)	Nombre de véhicules	ECC	ECD
[80 ; 100 [ [100 ; 120 [ [120 ; 130 [ [130 ; 140 [ [140 ; 150 [ [150 ; 170 [ [170 ; 190 [	120 90 100 120 40 20 10	120 210 310 430 470 490 500	500 380 290 190 70 30 10
Total	500

Le graphique des ECD et ECC est :

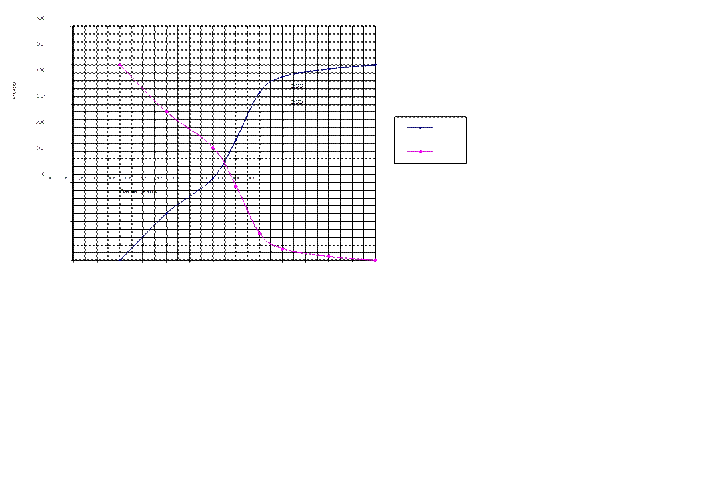Graphiquement on peut lire que la valeur de la médiane est environ 125 km/h.

C'est cette valeur qui partage l'effectif en deux soit 250 (graphiquement on lit un peu plus ).

Mais la lecture graphique est imprécise parfois, il est donc nécessaire d'avoir recours aux calculs pour pouvoir déterminer la valeur de cette médiane.

Détermination de la médiane par le calcul

Dans l'exemple qui nous intéresse, l'effectif total est 500.

Il va donc falloir trouver la valeur de la vitesse qui partage l'effectif en deux soit 250.

D'après le tableau des ECC, le 250^e véhicule se trouve dans la classe [120 ; 130[.

La valeur de la médiane est donc situé dans cet intervalle.

Dans l'intervalle [120 ; 130[ il y a 100 véhicules, le 250^e véhicule occupe la 40^eme place dans cet intervalle.

Pour déterminer la valeur de la médiane, on va considérer que les 100 véhicules de la classe [120 ; 130 [ se répartissent de manière uniforme :

Il y a 10 km/h d'écart entre 120 km/h et 130 km/h et 100 véhicules dans cet intervalle donc chaque véhicule sera espacé de:

Si on regroupe ce qui se passe dans une tableau :

Rang du véhicule parmi la totalité	Rang du véhicule dans la classe [120 ; 130 [	Vitesse du véhicule
211 212 213 214 215 216 217 ………………...ect…………….. 248 249 250	1 2 3 4 5 6 7 ………………...ect…………….. 38 39 40	120 120,1 120,2 120,3 120,4 120,5 120,6 ………………...ect…………….. 123,8 123,9 124

La valeur de la médiane est donc de 124 km/h.

On peut la calculer de la manière suivante :

La vitesse du premier véhicule dans la classe [120 ; 130[ est 120 km/h.

Or on sait que le 250^e occupe la 40^eme place dans cet intervalle. Etant donné que les véhicules se répartissent tous les 0,1 km/h, sa vitesse sera donc 120 + 40 ´ 0,1 = 120 + 4 = 124 km/h.

TRAVAUX AUTO FORMATIFS :

CONTROLE :

Donner la définition de la médiane ?

Comment calcule –t- on la médiane ?

EVALUATION

1- soit le tableau ci -dessous On demande  : 1°) Evaluer le rang de la médiane . 2°) Rechercher la classe correspondante au rang trouvé 3°) Trouver la valeur exacte de la médiane. Par le calcul puis de vérifier le résultat par le graphique.
	x i	Effectifs ( n i )
		Simples	Cumulées Croissantes	Cumulées décroissantes
	] 1000 - 1500 ]	6	6	65
	] 1500 - 2000 ]	12	18	59
	] 2000 - 2500 ]	25	43	47
	] 2 500 - 3000]	17	60	22
	] 3000 - 3500 ]	5	65	5
		65

3°) Soit une série statistique ordonnée, le nombre de donnée est de 25 :

a) Que peut -on conclure à partir de l’énoncé :

b) Quelle le rang de la médiane ?

2°) Déterminer la valeur de la médiane par le calcul ; puis vérifier par le graphique.

Les mesures sont des observations qui informent

Limites des classes	Valeurs centrales		Effectifs: ni	Calcul : appelé calcul des « Fréquences »
158-162	160 =		n1 = 2		= 0,07 (à 0,01près)
163-167	165		n2 = 4		= 0,13
168-172	170		n3 = 5		= 0,17
173-177	175		n4 = 9		= 0,3
178-182	180		n5 = 6		= 0,2
183-187	185		n6 = 3		= 0,1
188-190	190		n7 = 1		= 0,03
total			N = 30	Somme des fréquences = 1

CORRIGE :

3°) Soit une série statistique ordonnée, le nombre de donnée est de 25 :

a) Que peut -on conclure à partir de l’énoncé : il y a le même nombre de données de part et d'autre de la "médiane".

b) quelle le rang de la médiane ? Ainsi, si dans une série statistique qui a 25 données la médiane est la treizième valeur.

(12 données Ü médianeÞ 12 données)