|
COMPLEMENTS SUR
LA MEDIANE |
|
Ce compléments a pour but de vous montrer comment on peut calculer la va leur de la médiane.
Rappel La médiane d'une série statistique est la valeur de la variable telle que le nombre de valeurs qui lui sont inférieurs est égal au nombre de valeurs qui lui sont supérieurs.
Graphiquement on peut déterminer sa valeur à l'aide du graphique des effectifs cumulés croissants et décroissants : La médiane est alors la valeur de l'abscisse du point d'intersection de ces deux courbes.
Prenons un exemple : Une distribution statistique a été établie après un contrôle radar sur autoroute, on a classé les données ( regroupées en classes) dans le tableau suivant :
|
Vitesse ( km/h) |
Nombre de
véhicules |
|
[80 ; 100 [ [100 ; 120 [ [120 ; 130 [ [130 ; 140 [ (140 ; 150 [ [150 ; 170 [ [170 ; 190 [ |
120 90 100 120 40 20 10 |
|
Total |
500 |
Si on complète ce tableau à l'aide des ECD et ECC :
|
Vitesse ( km/h) |
Nombre de
véhicules |
ECC |
ECD |
|
[80 ; 100 [ [100 ; 120 [ [120 ; 130 [ [130 ; 140 [ [140 ; 150 [ [150 ; 170 [ [170 ; 190 [ |
120 90 100 120 40 20 10 |
120 210 310 430 470 490 500 |
500 380 290 190 70 30 10 |
|
Total |
500 |
|
|
Le graphique des ECD et ECC est :
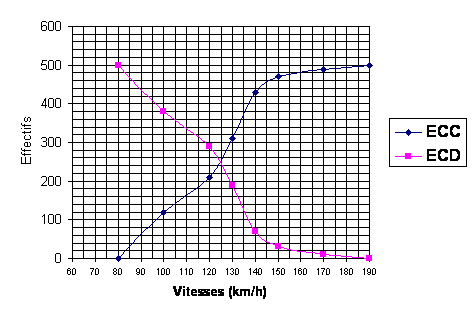 Graphiquement
on peut lire que la valeur de la médiane est environ 125 km/h.
Graphiquement
on peut lire que la valeur de la médiane est environ 125 km/h.
C'est cette valeur qui partage l'effectif en deux soit 250 (graphiquement on lit un peu plus ).
Mais la lecture graphique est imprécise parfois, il est donc
nécessaire d'avoir recours aux calculs pour pouvoir déterminer la valeur de
cette médiane.