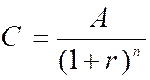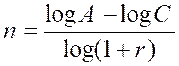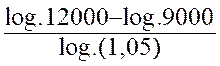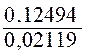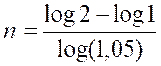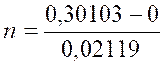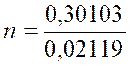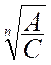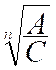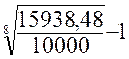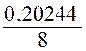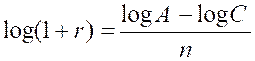Pré
requis:
|
|
|
|
|
|
|
Les suites
géométriques |
|
|
Les suites
arithmétiques |
|
|
|
|
|
Les puissances de
dix |
ENVIRONNEMENT
du dossier :
|
Objectif précédent Etude simple |
Suivant : 1°) Etude simple sur les log. Et expo |
||
|
|
|
|
|
|
|
|
|
|
Module : LES
INTERETS COMPOSES
|
TEST |
COURS |
Interdisciplinarité |
|
COURS
MATH
FINANCIERE :
Les mathématiques financières mettent en relation une personne (morale
ou physique ) qui prête une somme d ’argent ( appelée :
« prêteur » ) et une personne qui « emprunte cet argent (appelée « emprunteur » ) .
La somme d’argent prêtée ( appelée « capital ») rapporte de l’argent à
celui qui le prête. ( noté : C )
L’argent est prêté a un « certain »
taux exprimé en pourcentage .Le taux est « l’intérêt » produit par un
capital de 100 euros placés pendant un an.
L’intérêt est proportionnel au capital .
Cet intérêt est appelé
« loyer de l’argent » (ce
loyer de l’argent varie ,il est fixé par l’état ou les
banques.)
Il
existe deux types d’intérêt :
les intérêts simples : l’intérêt est dit « simple »
lorsqu’il est proportionnel à la durée du prêt.
Les intérêts composés :
l’intérêt est dit « composé »
si à la fin de chaque année , l ’ intérêt
simple produit pendant l’année précédente
est ajouté au capital, cet intérêt produisant à son tour des intérêts.
(on dit alors que l’intérêt est « capitalisé » .)
LES
INTERETS COMPOSES:
En arithmétique il a été
dit qu’un capital est placé à intérêts composés lorsqu’à la fin de chaque année
les intérêts s’ajoutent au capital de manière à
augmenter celui-ci .
|
|
Autrement
dit : Un capital est placé à intérêts composés ,
lorsque à la fin de chaque année , l’intérêt s’ajoute au capital pour
produire lui-même de l’intérêt. On dit encore que l’intérêt est capitalisé à
la fin de chaque année. Exemple :
Une personne place 1 000 euros à 5 % . Au bout
d’un an ce capital a produit un intérêt de 50 euros. Si la personne ne
perçoit pas ces 50 euros , ils s’ajoutent au capital
qui devient 1050 euros. A la fin de la seconde année ce capital de 1050 euros à produit un intérêt de 0,05 euros fois 1050 = 52,50 euros. Cet intérêt s’ajoutant de nouveau au capital celui-ci devient 1 102, 50 euros .
C’est ce capital qui portera intérêt pendant la troisième année et ainsi de
suite. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Problème
1 : Quelle est la valeur « A » acquise au bout de
« n » années par un capital « C » placé à intérêts
composés au taux « t » . Nous posons r = La valeur acquise par 1 euro est « 1 + r » ;
la valeur acquise de « C » euros est « C ( 1 + r
) » Ainsi
la valeur acquise par un capital au bout d’un an est égale au produit de ce
capital par ( 1 + r ) Valeur acquise par le capital
« a » au bout de la 2ème
année . |
|
|||||||||||||
|
|
|
C ( 1 + r ) |
( 1 + r )
= |
C ( 1 + r ) 2 |
|
|
|||||||||
|
|
|
Capital
au début de la 2ème année |
|
|
|
|
|||||||||
|
|
Valeur
acquise par le capital « a » au bout de la 3ème année . |
|
|
||||||||||||
|
|
|
C ( 1 + r ) 2 |
( 1 + r )
= |
C ( 1 + r ) 3 |
|
|
|||||||||
|
|
|
Capital au début de la 3ème
année |
|
|
|
|
|||||||||
|
|
A la fin de la nème
année |
|
|
||||||||||||
|
|
|
|
A
= C
( 1 + r ) n =
C ( 1 + |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
Ou |
Log A
= log C + n log ( 1 + r ) |
( 1 ) |
|
|
||||||||||
|
|
Remarque : On convient d’appliquer la formule (1) dans tous les cas , même lorsque la durée du placement n’étant pas un
nombre entier d’années « n » est une fraction. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
Exemple : Si l’un de nos ancêtres avait placé il y a 200 ans « C= 100 euros » à intérêts
composés au taux de 6 % , de quel capital
disposerions nous actuellement en admettant qu’il ait pu nous être transmis
sans prélèvement ? |
|
|||||||||||||
|
|
|
Appliquons la formule ( 1 ) |
Log
A =
log C + n log ( 1 + r ) |
|
|
|
|||||||||
|
|
|
|
Log
A =
log 100 + 200 log ( 1 ,06 ) |
|
|
|
|||||||||
|
|
|
|
Log 1,06 = 0,025306 |
Log 1,06 = 0,025306 |
|
|
|||||||||
|
|
|
|
|
200 Log 1,06 = 5,0612 |
Log A = 7 , 061 206 |
|
|||||||||
|
|
|
|
|
Log 100 = 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Sur la calculatrice : |
Taper :
7 , 061 206
inverse log = 11
513 463 euros ,804840153715497477250398 |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|||||||||||||
|
|
Généralisation :
Soit « C » le capital placé , « A » ce que
devient le capital augmenté de ses intérêts composés au bout de « n »
années ; « r »
l’intérêt de 1 franc. Ou ( euro : € ) Le capital « A » , au bout d’un an , sera devenu C ( 1 + r ) Le capital « A » , au bout de deux
ans , sera devenu : C ( 1+ r) ( 1+ r) Ou A =
C ( 1 +
r ) 2 Le capital « A » , au bout de 3
ans , sera devenu : C ( 1+ r)2 ( 1+ r) Ou A =
C ( 1 +
r ) 3 Et ainsi de suite
. Si l’on représente par
« A » , ce que devient le capital « C » au bout de
« n » années , on aura l’expression : A = C ( 1+ r ) n ou
A = C ( 1 + Si l’on utilise les logarithmes : on peut
écrire : Log A
= log C + n log ( 1 + r ) (1) |
|
|||||||||||||
|
I)
Calcul de la valeur obtenue ( A ) par le capital placé « C » : |
|
||||||||||||||
|
|
On applique la formule : A = C ( 1 + r ) n ou
A = C (
1 + Problème
1 : Que devient , après 15 ans , une somme de 8000 euros
placée à intérêts composés à 5 % ? Solution 1
: La quantité inconnue est A . Appliquons la formule : ( on utilise la
calculatrice scientifique) A = 8 000 ( 1
+ 0,05)15 A = 8000 (2,078928179411367257720947265625) A = 16631,425435290938061767578125 A = 16 632 euros à 1 euro
prés . Commentaire
sur l’analyse du résultat obtenu : on voit qu’une somme placée à
intérêts composés à 5 %
est plus que doublée au bout de 15 ans . |
|
|||||||||||||
|
Pour
effectuer le calcul précédent , on peut : Solution
1 : Trouver la 15ème
puissance de 1,05 soit avec la
calculatrice scientifique ou dans une table d’intérêts composés . Solution
2 : Effectuer le calcul par les logarithmes . |
|||||||||||||||
|
|
Solution 2 Calcul par les logarithmes : On a à effectuer : A = 8 000 ( 1,05)15 On posera : log A = log. 8
000 + log 15 log 1,05
- calculatrice : recherche du log. 8 000 = 3,90309 ………………= . 3,90309
- calculatrice recherche du 15
log. 1,05 = 0,02119
Total : log A =
3,90309 + 0,31785 Log
A =
4 ,22094 Recherche de « A » Avec la
calculatrice : Soit A = inv. log 4 ,22094 ;
A = : 16631
, 828572937439225613768710988 Avec la table des log. : Le nombre correspondant au log.
4,22094 est , d’après la table : 16632 Conclusion : A
= 16 632 euros à 1
euros prés . |
|
|||||||||||||
|
II)
Calcul du capital placé « C » : |
|
||||||||||||||
|
|
De la
formule (1) on obtient
la formule suivante :
|
|
|||||||||||||
|
|
De la formule ( 2 ) Log A
= log C + n log ( 1 + r ) ,
par transformation , on obtient :
log C = Log A - n log ( 1 + r
) |
|
|||||||||||||
|
|
on en
tire la formule (2): log C = Log A + n
colog ( 1 + r ) (3) |
|
|||||||||||||
|
|
Exemple :
Quel capital convient-il de placer à intérêts composés au taux de 5 % lors de
la naissance d’un enfant pour lui assurer 25 ans plus tard , une dote de 100
000 |
|
|||||||||||||
|
|
Appliquons la formule ( 2 ) :
log C = Log A - n log ( 1 + r )
log C = Log 100 000 - 25
log ( 1,05
) |
|
|||||||||||||
|
|
Calculs
intermédiaire : |
Log 1,05 = 0 , 021189 |
25 log 1,05
= 0,529725 |
|
|||||||||||
|
|
Log A 100 000 = 5 |
Log C = 5 -
0,529725 Log C = 4, 470275 |
|||||||||||||
|
|
C = inv. log 4, 470275 |
29530,785562960727707751789757064 |
|||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
Soit
le capital à placer : |
29 531
euros. |
|
|||||||||||
|
|
|
|
|||||||||||||
III ) CALCUL
DU TEMPS ou de « n »
|
|
||||||||||||||
|
|
Dans la formule : A = C ( 1+ r ) n on peut déterminer la valeur de
« n » . On a : ( 1+ r ) n = Et en appliquant le calcul :
« n » fois le log. ( 1 + r) = log. A – log. C et |
|
|||||||||||||
|
|
Problème 1: Un capital de 9 000 euros a produit , capital
et intérêts composés , une somme de 12 000 euros , le taux étant de 5 % . Combien
d’années est-il resté placé ? Solution : On aura , d’après la formule : 12 000 = 9000 et en appliquant le calcul logarithmique : n = on a log 12000 = 4,07918 et log. 9000 = 3,95424 reste : log :
0,12494 Or log. 1,05 =
0,02119 On aura donc à effectuer la division d’un logarithme par un autre
logarithme :
|
|
|||||||||||||
|
|
Problème 2: Au bout de combien de temps un capital placé à
5% d’intérêts composés doublera – t
–il de valeur ? |
|
|||||||||||||
|
|
Solution : |
|
|||||||||||||
|
|
Prenons pour unité le capital placé « C » = 1
et A = 2 |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Appliquons la formule ci-dessus : |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||
|
Log 2 = 0,30103 |
|
|
|||||||||||||
|
Log 1 = 0 |
|
|
|||||||||||||
|
Log 1,05 =
0,02119 |
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Log n = log 0,30103 - log 0,02119 |
|
|||||||||||||
|
|
log 0,30103 = -
0,52139022139877202145213797217432 |
|
Log n = (-
0,52139022139877202145213797217432 ) - (-1,6738690432892054231534034061317) |
|
|||||||||||
|
log 0,02119 = -1,6738690432892054231534034061317 |
|
Log n = 1,1524787786012279785478620278257 |
|||||||||||||
|
|
« n = 14,206227937433240939310643298711 »
année |
|
|||||||||||||
|
|
Soit
: 14 ans + ( 0, 206227937433240939310643298711
fois 360) = n =
soit 14 ans 74,2 jours |
|
|||||||||||||
|
|
« n = = soit 14 ans 74,2
jours » |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Pour qu’un placement rapporte 3 fois le fond de départ :
combien d’année doit durer un prêt :? |
|
|||||||||||||
|
|
Pour qu’un placement rapporte 4 fois le fond de départ :
combien d’année doit durer un prêt :? |
|
|||||||||||||
|
|
Pour qu’un placement rapporte 5 fois le fond de départ :
combien d’année doit durer un prêt : ? |
|
|||||||||||||
|
|
Pour qu’un placement rapporte 6
fois le fond de départ : combien d’année doit durer un prêt : ? |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
III) CALCUL DU TAUX ou DE
« r » |
|
||||||||||||||
|
|
Dans la formule : A = C ( 1+ r ) n on peut déterminer la
valeur de « r » . On a : ( 1+ r ) n = ( 1 + r ) = et r
=
Il faudra chercher la valeur de
|
|
|||||||||||||
|
|
Problème . 1 : A
quel taux faut-il placer un capital de 10 000 € ,
pour qu’il produise , capital et intérêts composés , une somme de 15 938 , 48
€ en 8 ans . Solution :*On aura , d’après la formule : 15 938,48 = 10 000 ( 1+ r ) n D’où r = Par calcul logarithmique ,
on a : log.15 938
, 48 = 4,20244 log .
10 000 = 4 différence : log. 0,20244 Ce logarithme doit être divisé par 8 , on a Au logarithme correspond le nombre 1,06 Retranchons l’unité , et
on a : r = 0,06 Le taux était de 6 % |
|
|||||||||||||
|
|
Problème . 2 : A
quel taux ……………. ? Ayant calculé
( 1 + r ) on en déduit facilement
« r » . Ce
problème n’a pas d’application pratique , on retiendra
qu’ un placement s’effectuant
au taux le plus avantageux. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
TRAVAUX AUTO
FORMATIFS.
CONTROLE
Soit expression : A = C ( 1+ r ) n
Que signifie chaque lettre ?
« C »,
« A »
« n »
; « r »
Transformer la formule précédente pour
obtenir :
C = ? ; r = ? ; n = ?
EVALUATION :
Problème 1 :
Que devient , après 15 ans , une somme de 8000 euros placée à intérêts composés à 5 % ?
Problème 2:
Un capital de 9 000 euros a produit
, capital et intérêts composés , une somme de 12 000 euros , le taux
étant de 5 % . Combien d’années est-il resté placé ?
Problème 3 .
A
quel taux faut-il placer un capital de 10 000 € , pour
qu’il produise , capital et intérêts composés , une somme de 15 938 , 48 € en 8
ans .