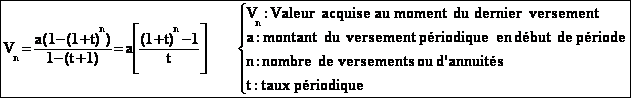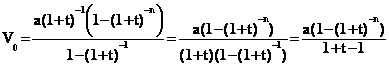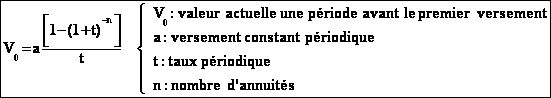LES ANNUITES-EMPRUNTS

Résumé cours (niveau 4)

LES ANNUITES

	I )PRINCIPE DES ANNUITES
	Définition ; +Exemple; +Généralisation : capitalisation avec versement en fin de période ; +Annuités et valeur acquise ; II ) Exercices d'application.
	III ) Actualisation d' une suite d' annuités constantes +But ; Exemple ; +Cas général ; +Annuité et valeur actuelle : A ) Exercices d'application ;
	IV )RENTABILITE D' UN INVESTISSEMENT +But : Exemple ; +Cas général
	+Annuité et valeur actuelle
	V )RENTABILITE D' UN INVESTISSEMENT valeur nette actualisée (VNA ou VAN) ; Exercice

COURS.

I )PRINCIPE DES ANNUITES

Définition : On appelle annuités des sommes payables de façon périodique ( à intervalles de temps déterminés et constants ). Les annuités peuvent servir à :

- Constituer un capital.

- Rembourser une dette.

+Exemple

Monsieur Dupont décide de constituer un capital en versant chaque année au 1^er janvier une somme de 12000 € pendant 10 ans. Les fonds sont bloqués et rémunérés au taux de 8,5 % annuel. Il s'agit alors de calculer le capital constitué lors du dernier versement..

Le premier versement a₁ aura acquis 9 ans plus tard la valeur :

12 000 ´ (1,085)⁹

Le second versement a₂ aura acquis 8 ans plus tard la valeur :

12 000 ´ (1,085)⁸

ect……

Le capital total disponible sera donc :

V₁₀ = 12 000 ´ (1,085)⁹ + 12 000 ´ (1,085)⁸ + ……+ 12 000.

Cette expression est la somme des termes d'une suite géométrique de 10 termes, de terme

U₁ = 12 000 et de raison 1,085.

En appliquant la formule de calcul ( voir chapitre 4°)) on a :

€

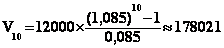+Généralisation : capitalisation avec versement en fin de période

Rappel : La somme des k premiers termes d'une suite géométrique de raison q et de premier terme U₁ est :

On considère une suite de n annuités constantes d'un montant a, versées en fin de période, le taux périodique est i.

On appelle V_n la valeur acquise au moment du dernier versement :

Au bout d'un an : n = 1 : V₁ = a(1+i) + a

Au bout de deux ans : : n = 2 : V₂ = V₁(1+i) + a = a(1+i)² + a(1+i) + a

Au bout de trois années : n = 3 : V₃ = V₂ (1 + i ) = a(1+i)³ + a(1+i)²+ a(1+i) +a

…………………………….

Au bout de n années : V_n = a(1+i)ⁿ + a(1+i)^n-1 +….+ a

On remarque que V_n est la somme des n premiers termes d'une suite géométrique de premier terme a et de raison (1+i), d'après la formule rappelée plus haut on a :

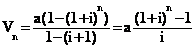
+Annuités et valeur acquise

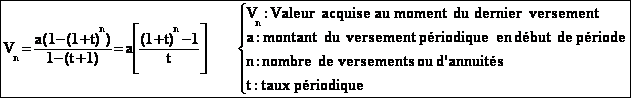
II ) Exercices d'application

1°) On verse 1000 € chaque année pendant 8 ans. Calculer la valeur acquise au moment du dernier versement.(Capitalisation annuelle, taux annuel : 2 %)

Réponse : 8582,97 €

2°) Une personne verse 150 € par mois pendant 3 ans. Calculer la valeur acquise au moment du dernier versement.(Capitalisation mensuelle, taux mensuel : 0,4 %)

Réponse : 5 795,72 €

3°) Afin d'acquérir un capital de 13000 €, on effectue 10 versements constants annuels, au taux annuel de 5 %. Quel est le montant de chaque annuité ?( Capitalisation annuelle)

Réponse : 1 033,56 €

4°) On verse chaque trimestre 230 €. Le taux d'intérêts trimestriels est de 0,5 %. La valeur acquise au moment du dernier versement est de 2 837,18 €. Calculer le nombre de versements trimestriels.

Réponse : 12 versements

III ) Actualisation d' une suite d' annuités constantes

+But : Calculer la valeur actuelle d'une suite d'annuités constantes, une période avant le premier versement.

+Exemple : Monsieur Warmé doit rembourser une somme empruntée en versant trois semestrialités d'un montant de 1 591 €. Le premier versement a lieu 1 semestre après l'emprunt.

Le taux semestriel est de 3 % et la capitalisation est semestrielle.

On veut calculer le capital emprunté.

Le remboursement est égal à la sommes des valeurs actuelles des trois remboursements :

Valeur actuelle du premier versement : 1 591 ´ 1,03^-1

Valeur actuelle du second versement : 1 591 ´ 1,03^-2

Valeur actuelle du dernier versement : 1 591 ´ 1,03^-3

Le capital emprunté est donc : 1 591 ´ 1,03^-1 +1 591 ´ 1,03^-2 + 1 591 ´ 1,03^-3 » 4 500 €

+Cas général : Le remboursement d'un capital emprunté est constitué par une suite de n annuités constantes, de valeur a. le taux période est t.

Le premier remboursement est effectué une période après l'emprunt.

Le capital emprunté est égal à la somme des valeurs actuelles des n versements :

Valeur actuelle du 1^er versement : a(1+t)^-1

Valeur actuelle du 2^eme versement : a(1+t)^-2

……..

Valeur actuelle du n^eme versement : a(1+t)^-n

Le capital emprunté V₀ est : V₀ = a(1+t)^-1 + a(1+t)^-2 + …..+ a(1+t)^-n

On reconnaît la somme des termes d'une suite géométrique de raison (1+t)^-1 et de premier terme a(1+t)^-1. En appliquant la formule rappelée plus haut (U₁ = a(1+t)^-1 et q = (1+t)^-1 )on a :

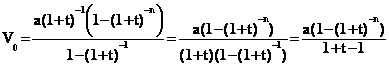
Ainsi :

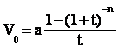
+Annuité et valeur actuelle :

La valeur actuelle V₀ d'une suite de n annuités de montant a, une période avant le premier versement est :

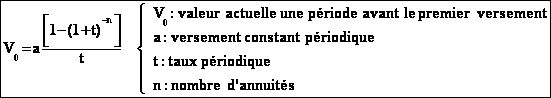
A ) Exercices d'application

1°) Pour rembourser un emprunt, on verse 10 mensualités constantes de 304,14 € au taux mensuel de 0,25 %. Le premier versement intervient 1 mois après l'emprunt. Calculer le montant de l'emprunt.

Réponse : 3 000 €

2°) Une personne s'engage à rembourser une dette de 1 830 € par des versements constants trimestriels sur 18 mois. Quel est le montant d'une trimestrialité si le taux trimestriel est de 0,75 % ? Le premier versement s'effectue 1 trimestre après l'emprunt.

Réponse : 313,06 €

3°) Combien de versements semestriels de 1 060,79 € une personne doit-elle effectuer pour rembourser un emprunt de 5 000 € ?

Premier versement : un semestre après l'emprunt; Taux semestriel : 2 %, capitalisation semestrielle.

Réponse : 5 versements.

IV )RENTABILITE D' UN INVESTISSEMENT

+1^erExemple : Une entreprise de transport investit 183 000 € au début de l'année 2000. Les rentrées nettes annuelles dégagées par cet investissement sont estimées à 44 000 € à la fin de chaque année pendant 5 ans.

Un investissement est rentable s'il rapporte plus d'argent qu'il n'en coûte.

Pour pouvoir comparer les sommes dépensées et les rentrées nettes dégagées, il faut les actualiser à la date de l'investissement : début 2000. On prend comme taux annuel 3,5 %.

Valeur actuelle de la rentrée 2000 : 44 000 1,035 ^-1 » 42 512

Valeur actuelle de la rentrée 2001 : 44 000 1,035 ^-2 » 41 074

Valeur actuelle de la rentrée 2002 : 44 000 1,035 ^-3 » 39 685

Valeur actuelle de la rentrée 2003 : 44 000 1,035 ^-4 » 38 343

Valeur actuelle de la rentrée 2004 : 44 000 1,035 ^-5 » 37 047

La somme de ces valeurs actuelles est : 198 661 €. Cette somme est supérieure au capital investi : L'investissement est rentable au taux de 3,5 %

La valeur nette actualisée (VNA ou VAN) est égale à 198 661 - 183 000 = 15 661 €

valeur nette actualisée (VNA ou VAN)

VNA = Somme des rentrés nettes actualisées - somme des capitaux investis actualisés

Si VNA > 0, L'investissement est rentable.

Si VNA < , L'investissement n'est pas rentable au taux utilisé.

Si VNA = 0, la taux d'actualisation est la taux de rentabilité interne (TRI)

Exercice :

Un dirigeant de PME décide d'investir 40 000 € puis 38 000 € l'année suivante pour l'achat de nouveaux matériels. Les rentrées nettes annuelles dégagées par cet investissement sont de 25 000 € pour chacune des trois années. La valeur résiduelle de ce matériel est de 10 000 € au bout des trois années.

1°) Déterminer la rentabilité de l'investissement aux taux annuels de 3% et 6%

2°) Vérifier que le taux de rentabilité interne est de 5,45 %

Indication : Rentrés nettes à actualiser : 25 000 €(1 an, 2ans et 3ans), 10 000 €(3ans)

Capitaux investis : 40 000 € et 38 000 € à actualiser(1 an)

Réponses : à 3 % VNA »2 973, 5 € ; à 6 % VNA »- 627,57 € ; A 5,45 € VNA »3,40 €