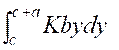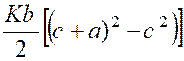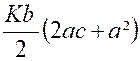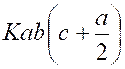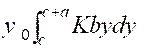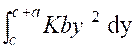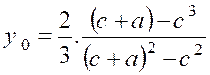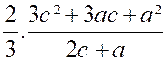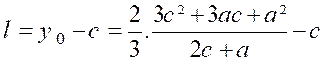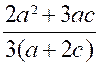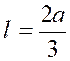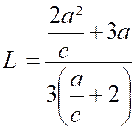COURS

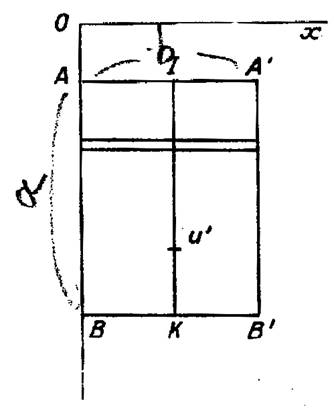
Soit une plaque rectangulaire (voir la figure ci contre) de dimensions :

«  A B =  a » ; « A A’ = b » , immergée verticalement dans l’eau , la surface libre de l’eau passant  par l’axe « O x » . On connaît la distance  «  OA = C » du bord supérieur de la plaque à la surface libre.

Cherchons la pression totale s’exerçant  sur la plaque .

On sait qu’en un point quelconque d’un liquide, la pression sur un élément de surface est égale au poids d’une colonne de liquide   , la pression sur un élément de surface  est égale au poids d’une colonne de liquide ayant pour section droite l’aire de l’élément et pour hauteur sa distance à la surface libre .

Partageons , par suite, l’aire du rectangle en petits éléments par des parallèles à « O x ». L’un d’eux , situé à la distance « y » de « O x » , a pour surface « b dy »

Tous les points étant à la même profondeur « y », il subit la pression «  K by dy » , en appelant « K » la densité du liquide.

La pression totale est donc :

  =    = 

Remarque :

La valeur de la pression peut se mettre sous la forme :   «  »

Elle est la même que si la plaque rectangulaire était immergé horizontalement à la même profondeur que son centre de gravité.

Soit, par exemple : OA = 2 mètres ; « AB = 5 mètres, « AA’ = 4 mètres »Le poids du mètre cube d’eau étant 1 000 kg , la pression sera :

1 000 fois 2 fois ( 2 fois 5 fois 2 + 25 )  = 90 000 kg.

Le centre de pression est , par définition, le point  d’application de la résultante de toutes les forces de pression normales à la plaque .

En prenant les moments de ces forces par rapport à l’ axe «  O x », on obtient l’ordonnée «  y₀ » du centre de pression cherché par la formule :

=   = 

d’où :

  =

Ce centre de pression «  »  est , par symétrie , sur l’axe « IK » du rectangle à une distance «   »  de la base supérieure donné par :

   =

En particulier, si « c » est nul, c'est-à-dire si le bord supérieur de la plaque est à la surface de l’eau , on a « .

Si « c » est très grand, en mettant « l » sous la forme :   , on voit que « l » tend vers «  ».

 Le centre de pression se confond alors avec le centre de gravité.

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Reprendre chaque exercice du cours.

Voir le cours !!!!!