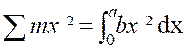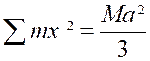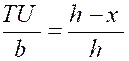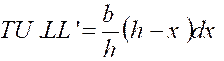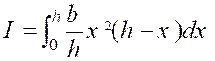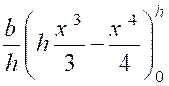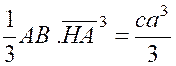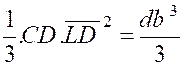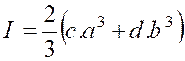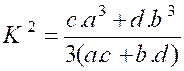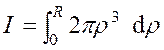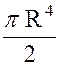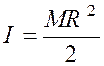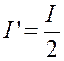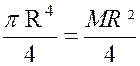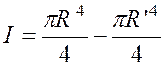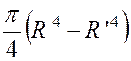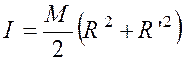Pré requis:
|
Info : liste des
connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°) L’intégration par parties. 5°) application géométrique
d’une intégrale simple :aires planes. |
APRES :
|
Complément
d’Info :
1°)
Liste des cours : prépa concours
A consulter pour
compléments : |
|
|
|
|
|
|
|
TITRE :niveau
III : LES INTEGRALES : APPLICATIONS
GEOMETRIQUES DES INTEGRALES SIMPLES :
LES MOMENTS D’INERTIE .
|
|
DEFINTION
. |
|
|
|
EXEMPLES : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Voir
l’évaluation !!! |
Contrôle |
évaluation |
|||
|
|
|
||
|
|
|
|
|
|
|
Le moment d’inertie d’un corps par rapport à un
point, un axe ou un plan est , par définition, la limite de la somme : «
Le rayon de giration est une longueur « R » telle que le moment
d’inertie ait pour valeur « M K
² » , « M »étant la masse totale du corps. Dans le cas usuel où le corps est homogène,on remplace habituellement la masse par « la
longueur » ; « la surface » ou « le volume »
suivant qu’il s’agit d’une ligne , d’une aire , ou d’un volume. |
|
|
|
|
DES EXEMPLES : |
|
|
|
|
Exemple 1 :
Moment d’inertie d’un rectangle par rapport à un côté. |
|
|
|
|
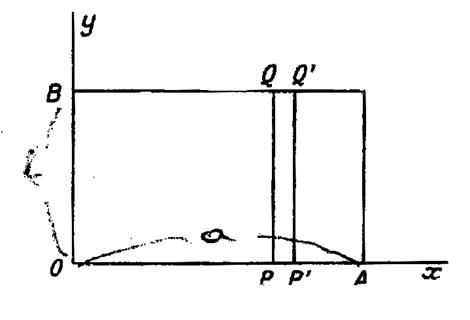
Soient « OA = a » et « OB = b » les côtés du
rectangle. Cherchons son moment d’inertie par rapport à
l’axe « Oy » En partageant la surface en éléments « P P ‘ Q ‘ Q »par des
parallèles à l’axe « O y », tous les points de l’un d’eux
sont à la même distance « x » , de l’axe
« O y » . Sa surface « P Q . P P’ = b dx »est son moment d’inertie est « Le moment d’inertie du rectangle est donc :
|
|
|
|
|
En appelant « M » la masse totale du rectangle , c'est-à-dire sa surface, on a « M =
ab » et « |
|
|
|
|
|
|
|
|
|
Exemple 2 :
Moment d’inertie ( I )
de la surface d’un triangle par rapport à sa base. |
|
|
|
|
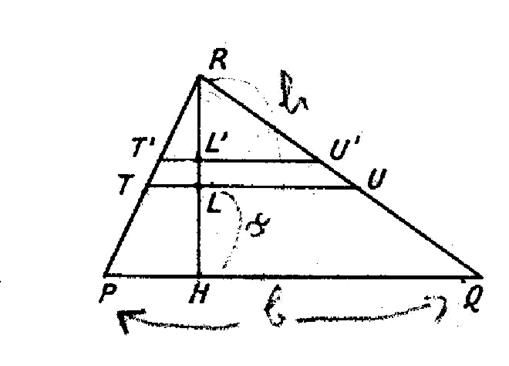
On désigne : ·
« b »
= « PQ » la base du triangle. ·
« h »
= « HR » sa hauteur. On demande : de calculer le moment d’inertie
de sa surface par rapport à « PQ » . Nous partageons le triangle en petites bandes
« T’U’ T U » assimilables à des
rectangles. On pose : « HL = x » ,on a
alors : L’élément d’aire est : |
|
|
|
|
Et |
|
|
|
|
|
|
|
|
|
Exemple 3 :
Moment d’inertie ( I )
de la surface d’une plaque en forme de
« T » , par rapport à son
axe . |
|
|
|
|
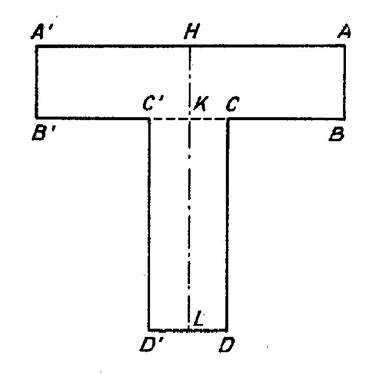
On donne : « AA’ = 2 a » ; « DD’ = 2
b » ; « AB = c » ; « CD = d » les dimensions de la plaque
. (voir la figure ci contre) Le moment d’inertie cherché est la somme des moments d’inertie
des quatre rectangles deux à deux égaux. Le rectangle « AHKB » a pour moment
d’inertie par rapport à « HK »
|
|
|
|
|
Le rectangle « LDCK » a , de même, pour moment d’inertie par rapport à
« KL » :
|
|
|
|
|
D’où le moment d’inertie cherché : |
|
|
|
|
D’autre part , la masse
« M » est la surface « 2 ( a.c + b.d) de la plaque . Et le rayon de
giration »R » est donné par : |
|
|
|
|
|
|
|
|
|
Exemple 4 :
Moment d’inertie ( I )
de la surface d’un cercle par rapport à son centre. |
|
|
|
|
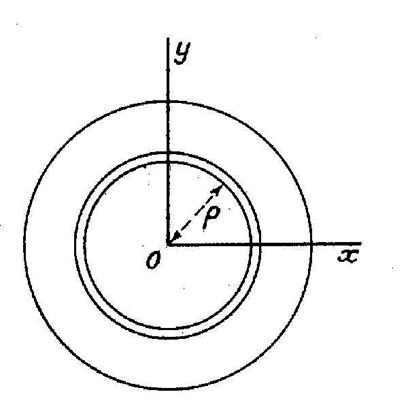
Nous partageons le cercle de rayon
« R » en couronnes concentriques .(voir la figure ci contre) Soit «
En désignant par « M » la masse du
cercle, c'est-à-dire sa surface « |
|
|
|
|
Remarque : Soit maintenant « I ’»
le moment d’inertie de la surface du cercle par rapport à un diamètre .Il est
facile de déduire « I ’» de « I ». En effet le moment d’inertie par rapport à
« O y », par exemple, est
« On a donc aussi : « D’autre part, le moment d’inertie par rapport au
centre est : « D’où
« |
|
|
|
|
Exemple 5 :
Moment d’inertie ( I )
d’ une couronne circulaire par rapport à un diamètre . |
|
|
|
|
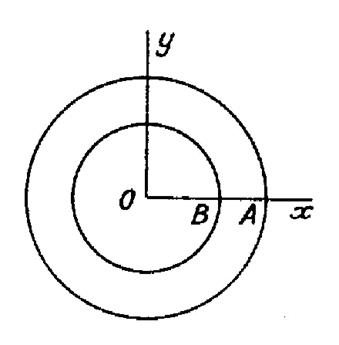
Soient « R = OA » et
« R’ = OB » , les deux rayons . ( voir la figure ci contre) Le moment d’inertie cherché est la différence
entre les moments d’inertie des deux cercles ,soit :
Si l’on veut exprimer ( I ) en fonction de la masse « M » ,
il faut remplacer la
surface : « D’où :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
Reprendre chaque exercice du cours. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||