|
DOC : Formation Individualisée
|
DOC : Elève. |
|
TRANSITION / COLLEGE / LYCEE. |
Information « TRAVAUX » |
|
OBJECTIFS :
- Savoir |
I ) Pré requis:
|
i9 |
:i |
II ) ENVIRONNEMENT
du dossier :
|
Dossier
précédent : |
Dossier
suivant : |
Info :retour vers
liste des résumés. |
III)
LECON n° : RESUME en
TRIGONOMETRIE
Chapitres :
IV)
INFORMATIONS « formation
leçon » :
|
Travaux auto - formation. |
|
Corrigé
des travaux auto - formation. |
||||
|
Corrigé |
||||||
V ) DEVOIRS
( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle : savoir » ; (remédiation) |
|
|
|
|
|
Devoir
sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents peuvent être
réutilisés ( tout ou partie) pour conclure une
formation .
|
Leçon |
Titre |
|
|
TRIGONOMETRIE |
|
RESUME |
|
Avant |
COSINUS D'UN ANGLE AIGU |
Après |
Première approche :
|
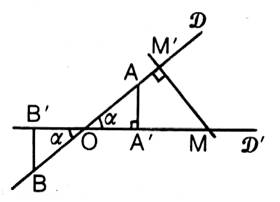
Deux droites sécantes et des segments et leurs
projetés. Dans la projection
orthogonale de la droite "D"
sur la droite "D' " , il y a
"proportionnalité des longueurs
entre segments et projetés. |
|
Le coefficient de proportionnalité est appelé : k
D'où le tableau de proportionnalité
|
´ k ¯ |
OA |
= |
OB |
¸ k |
|
|
OA' |
OB' |
On remarque que l'on a aussi OM' =
k OM M' est le projeté orthogonal
du point M sur la droite D.
On observera que le coefficient "k" ne dépend
que de la valeur de l'angle µ (lire: alpha). On
appellera le nombre "k"
cosinus de l'angle alpha. (Noté cos.µ)
En
conclusion : ![]()
Remarques : On observera que cos 90° = 0 et cos.0° = 1 ; d'où
0 "d cos.µ "d 1
|
Avant |
Les relations trigonométriques
dans le triangle rectangle. |
Angles :
- Dans un triangle la somme des angles sont
supplémentaires : 90° + ![]() +
+ ![]() = 180°
= 180°
- Dans un triangle rectangle la somme des deux angles
aigus sont dit "complémentaires" soit ![]() +
+ ![]() = 90°
= 90°
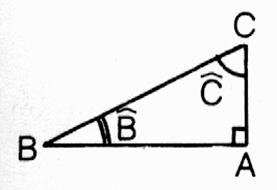
Côtés : Vocabulaire: 3 côtés ; 5 noms à connaître.
|
BC est appelée : Hypoténuse BA est le côté opposé à l'ouverture ou la fermeture
de l'angle a ( dit : côté opposé à a) BA est le côté adjacent à l'angle b AC est le côté opposé à l'angle b AC est le côté
adjacent à l'angle a. |
|
Remarques: l'hypoténuse est le côté
opposé à l'angle droit, BA et AC sont les côtés
"adjacents" à l'angle droit.
· COSINUS d'un angle :
Dans un
triangle rectangle. le
cosinus est égal au rapport de la longueur
du côté adjacent à l'angle considéré par la longueur de l'hypoténuse.
(Le cosinus est un nombre inférieur à 1)
|
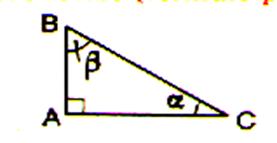
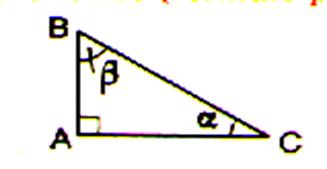
Relation
: appliqué
au triangle ABC ce donne : |
|
|
|
|
· SINUS d'un angle :
Dans un triangle
rectangle. le sinus est égal au rapport de la
longueur du côté opposé à l'angle
considéré par la longueur de l'hypoténuse.
(Le sinus est un nombre inférieur à 1)
|
Relation
: appliqué
au triangle ABC ce donne : |
|
|
|
|
· Tangente d'un angle :
Dans un triangle
rectangle. La tangente est égale
au rapport de la longueur du côté opposé
à l'angle considéré par la longueur du côté adjacent.
|
Relation
: appliqué
au triangle ABC ce donne : |
|
|
|
|
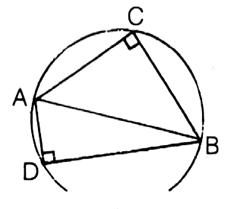
· On montre
que ![]() ;
parce que :
;
parce que : 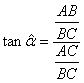
· On montre
que 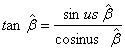 ;
parce que :
;
parce que : 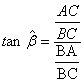
le sinus et le cosinus d'un angle aigu
sont des nombres compris entre 0 et 1 .
· Quelque que soit l'angle aigu a : Cos² a + sin² a = 1; (cos² a = (cos a )²)
· Quelques
valeurs à connaître:
|
|
0° |
30° |
45° |
60° |
90° |
|
Sin. |
1 |
|
|
|
0 |
|
Cos. |
0 |
|
|
|
1 |
|
Tan. |
0 |
|
1 |
|
|
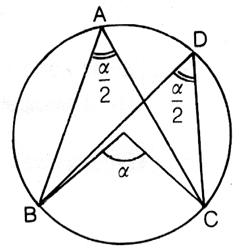
µ < 180°
|
Si |
|
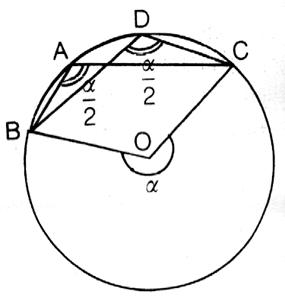
BC désigne l'arc intercepté par ![]() ou par
ou par ![]()
µ > 180°
|
Si
|
|
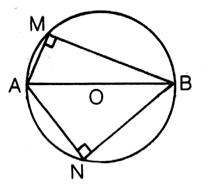
Cas particulier :
|
[AB] est un
diamètre du cercle ; on a alors pour
tout point M du cercle
|
|
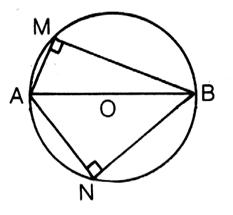
Deux cas importants :
|
Si |
|
|
Si |
|
|
Leçon |
Titre |
|
N° |
TRAVAUX d AUTO - FORMATION sur |
TRAVAUX N° d
AUTO - FORMATION : CONTROLE
TRAVAUX
N° d AUTO - FORMATION EVALUATION