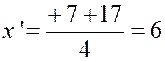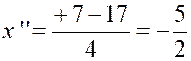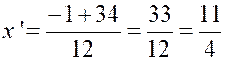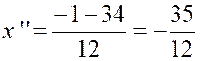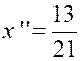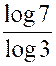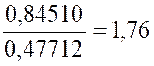Pré requis:

Les logarithmes : notions

Index

Objectif précédent Résoudre une équation du second degré. De la forme : ax² + bx + c

Objectifs suivants: Les annuités

Tableau  : TOUT sur les log.

DOSSIER : « Résoudre » LES EQUATIONS LOGARITHMIQUES.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité : Les intérêts composés.

Corrigé Contrôle

Corrigé évaluation

INFORMATIONS

Ce cours traite la résolution de quelques types d’équations . Les résolutions imposent aux solutions des restrictions du fait que les nombres négatifs ainsi que le « zéro » n’ont pas de logarithmes .

COURS

Exemple 1 : résoudre : log ( x – 5) + log ( 2x -3) = log 15
Les conditions restrictives sont :	x - 5 > 0 ; x > 5
	2x + 3 > 0 ; x >		La condition la plus restrictive est donc x > 5
En remontant des logarithmes aux nombres on est conduit à l’équation :
		( x – 5 ) ( 2 x + 3 ) = 15 soit : 2 x² + 3 x – 10 x – 15 = 15 2 x² - 7 x - 30 = 0
Cette équation du second degré a deux solutions : et la première solution sera retenue ; la seconde solution sera écartée.

Exemple 2  : résoudre : log ( 2x – 5) + log ( 3 x + 8 ) = 3 log 2 Or nous pouvons écrire : 3 log 2 = log 2 ^3 En tenant compte de cette remarque : l’équation proposée s’écrit : log ( 2x – 5) + log ( 3 x + 8 ) = log 2 ^3
Les conditions restrictives sont :	2 x - 5 > 0 ; x >
	3 x + 8 > 0 ; x >		La condition la plus restrictive est donc x >
En remontant des logarithmes aux nombres on est conduit à l’équation :
		( 2x – 5 ) ( 3 x + 8 ) = 2 ^3 soit : 6 x² + 16 x – 15 x – 40 = 8 6 x² - x - 48 = 0
Cette équation du second degré a deux solutions : et la première solution sera retenue  ; la seconde solution sera écartée.

Exemple 3  : résoudre : log ( 7x – 9)² + log ( 3 x - 4 )² = 2 En tenant compte de cette remarque : l’équation proposée s’écrit : 2 log ( 7x – 9) + 2 log ( 3 x -4 ) = 2 En divisant tous les termes par « 2 » on obtient : log ( 7x – 9) + log ( 3 x -4 ) = 1 en remplaçant « 1 » par « log 10 » on obtient : log ( 7x – 9) + log ( 3 x -4 ) = log 10
Les conditions restrictives sont :	7 x – 9 > 0 ; x >
	3 x -4 > 0 ; x >		La condition la plus restrictive est donc x >
En remontant des logarithmes aux nombres on est conduit à l’équation :
		( 7x - 9 ) ( 3 x – 4 ) = 10 soit : 21 x² - 28 x – 27 x + 36 = 10 21 x² - 55 x + 26 = 0
Cette équation du second degré a deux solutions : et la première solution sera retenue « 2 » ; la seconde solution sera écartée.

Exemple 4 : Résoudre 3 ^2x - 5 ( 3^x) – 14 = 0

Posons X = 3^x  : ( 1) ; par conséquent 3 ^2x = X ² et l’ équation proposée devient : X ² - 5 X – 14 = 0

Elle admet comme solutions : X ‘ = + 7 ; et X ‘’ = - 2

Dans l’égalité ( 1 ) remplaçons X par +7 , il vient 3^x = 7

Prenons le logarithme des deux membres :

log 3^x = log 7

x log 3 = log 7

x =

x =

Nous ne remplacerons « X » par « – 2 » dans l’égalité ( 1) car nous serions amenés à prendre le logarithme d’un nombre négatif ce qui est impossible.

En remontant des logarithmes aux nombres on est conduit à l’équation :

Cette équation du second degré a deux solutions :

et

la première solution sera retenue « 2 » ; la seconde solution sera écartée.

TRAVAUX AUTO FORMATIFS :

CONTROLE :

Lire le cours

EVALUATION:

1 : Résoudre : log ( x – 5) + log ( 2x -3) = log 15

2  : Résoudre : log ( 2x – 5) + log ( 3 x + 8 ) = 3 log 2

3  : Résoudre : log ( 7x – 9)² + log ( 3 x - 4 )² = 2

4 : Résoudre 3 ^2x - 5 ( 3^x) – 14 = 0

( corrigé dans le cours)