|
Les suites géométriques |
|
|
Les suites arithmétiques |
|
|
Les puissances de dix |
ENVIRONNEMENT
du dossier:
|
Objectif précédent : |
Objectif suivant : |
DOSSIER : Les logarithmiques de « x »
I )
Avantages des logarithmes.
II )
Définition : « Logarithmes décimaux »
III ) PROPRIETES des logarithmes. ( les 3 théorèmes)
|
TEST |
COURS |
Interdisciplinarité |
|
I ) Avantages des logarithmes.
Remarquons que les opérations sur les nombres ,
si on les ramène aux opérations sur les logarithmes , sont ramenées à des opérations d’ordre moins élevé :
Une multiplication est remplacée par une addition ;
Une élévation à une puissance est remplacée par une
multiplication ;
Une division est remplacée par une soustraction : Une extraction de
racine est remplacée par une division.
S’il était possible d’obtenir rapidement le logarithme d’un nombre donné , et inversement d’obtenir le nombre dont le
logarithme est donné , toutes les opérations seraient diminuées de difficulté
grâce aux logarithmes .
Les tables de logarithmes remplissent ce rôle ,
lorsque l’on connaît les règles permettant de les utiliser .
Rappels :
« Suites géométriques »
(voir les pré requis)
nous ne considérons ici que les raisons
positives.
1°) La suite 2 ; 6 ; 18 , 54 ; 162 ,
où chaque nombre s’obtient en multipliant
le précédent par (+3) constitue
une progression géométrique de raison « 3 »
2°) La suite a
, aq , aq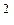 ;
aq
;
aq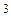 ,…..est
une progression géométrique de raison « q » .
,…..est
une progression géométrique de raison « q » .
Si « q » est supérieur à 1 , la
progression est dite « croissante ».
Exemple : pour « q » = 2
et a=5 ;nous obtenons : 5 ;
10 ; 20 ; 40 ; 80 ;…
Si « q » est inférieur à 1 , la
progression est dite « décroissante ».
Exemple : pour
« q » = ![]() et a=
2
et a=
2
Nous obtenons le début de la suite : 2 , 0,2 ;
0,02 ; 0 , 002 ;…
En résumé : une suite « géométrique » est une suite de
nombres tels que chacun d’eux s’obtient en multipliant le précédent par un
nombre constant appelé « raison »
3°)Le Système logarithmes
« base 10 » : appelé système des logarithmes vulgaires ou
logarithmes décimaux , ou encore appelé logarithmes de Briggs
II ) Définition : « Logarithmes décimaux »
Explication :
Ecrivons l’une au –dessous de l’autre :
1°) une progression
géométrique ayant un terme égal à 1 est pour raison 10 ;
2°)pour
une progression arithmétique ayant un terme égal à 0 et pour raison 1 , en
faisant correspondre au terme 1 de la première le terme 0 de la seconde :
|
géométrique |
…… |
0 ,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
…(1) |
|
Prog. arithmétique |
|
- 3 |
- 2 |
-1 |
0 |
1 |
2 |
3 |
..(2 ) |
Tout nombre de la
deuxième ligne est appelé le « logarithme décimale » du nombre
correspondant de la première ligne
Ainsi on écrira que (par
exemples)
Log
100 = 2
Log
0,1 = -1
« Le logarithme décimal de 100 est égal à 2 »
« Le logarithme décimal de 0,1 est égal à
-1 »
Imaginons qu’entre deux
nombres consécutifs de la 1er ligne et entre les deux nombres
correspondants de la deuxième ligne , on insère deux progression
formées du même nombre de termes :
|
Progression. géométrique |
…… |
10 |
a |
b |
c |
d |
100 |
….. |
e |
|
arithmétique |
|
1 |
a’ |
b’ |
c’ |
d’ |
2 |
|
|
Le terme
« x’ » de la deuxième ligne est le logarithme décimal du terme
correspondant « x » de la première ligne :
On écrira :
log x = x’
Examen des résultats précédents :
De l’examen des progressions (1 )
et (2 ) il résulte que :
1°) les nombres
négatifs n’ont pas de logarithmes.
2°)le
logarithme de 1 est égal à 0
3°) les logarithmes des
nombres positifs plus grand que 1 sont positifs.
4°)les
logarithmes des nombres positifs plus petits que 1 sont négatifs ;
5°)seules
les puissances de 10 ont pour
logarithmes des nombres entiers :
log 1000 = 3 ; log
0,0001 = - 4
III )
PROPRIETES des logarithmes.
Nous allons établir les
propriétés des logarithmes en utilisant les logarithmes des puissances de dix , mais ces propriétés s’appliquent aux logarithmes de
tous les nombres.
Théorème
1 :
Le logarithme d’un
produit de facteurs est égal à la somme
des logarithmes des facteurs.
Si nous
généralisons : log ( x ![]() y
y![]() z
) = log x + log y + log z
z
) = log x + log y + log z
Théorème 2 :
Le logarithme d’un
quotient est égal au logarithme d’un quotient est égal au logarithme du
dividende moins le logarithme du
diviseur.
Soit le quotient :
![]() =
q on sait que D = d
=
q on sait que D = d ![]() q
q
Appliquons le théorème
précédent
log D = log d + log q
On transforme : log q
= log D – log d
On peut donc écrire
que : log ![]() = log D – log d
= log D – log d
Théorème
3 :
Le logarithme d’une puissance d’un nombre est égal au produit du logarithme de ce
nombre par l’exposant de la puissance.
x![]() = x
= x![]() x
x![]() x
x![]() x
x![]() x
x
appliquons
: le
théorème relatif au produit des facteurs :
log x![]() = log x + log x + log x + log x + log x
= log x + log x + log x + log x + log x
soit (factorisons le deuxième
membre) log x![]() =
5 log x
=
5 log x
on
peut donc généraliser : log x![]() = n log
x
= n log
x
Théorème 4 : le logarithme
d’une racine d’un nombre
est égal au quotient du logarithme de ce nombre par l’indice de la racine .
Soit ![]() = x
= x
D’après la définition
de la racine « quatrième »
d’un nombre , cette égalité est équivalente à :
X = ![]() ou
à l’ égalité
équivalente :
ou
à l’ égalité
équivalente : ![]() = X
= X
|
|
en généralisant : log |
|
CONTROLE :
Compléter les phrases suivantes :
1°) les nombres
négatifs n’ont pas …………………..
2°)le
logarithme de 1 est égal à …………..
3°) les logarithmes des
nombres positifs plus grand que 1 ……………………..
4°)les
logarithmes des nombres positifs plus petits que 1 …………………………..
5°)seules les
puissances de 10 ont pour logarithmes
des nombres ………..
PROPRIETES
des logarithmes.
Théorème
1 :
Le logarithme d’un
produit de facteurs est égal à
Si nous
généralisons : log ( x ![]() y
y![]() z ) =
z ) =
Théorème 2 :
le logarithme d’un
quotient est égal au
On peut donc écrire
que : log ![]() =
=
Théorème
3 :
Le logarithme d’une puissance d’un nombre
est égal au.
on peut donc
généraliser : log a![]() =
=
Théorème 4 : le
logarithme d’une racine d’un
nombre est égal au
EVALUATION
Le logarithme décimal de 2 est 0 ,
30103
.
1°) quels sont les
logarithmes de 4 ; 5 ;
8 ; 16 , ; 20 ; 32 ; 40 ;
50 ?
2°) quels sont les
logarithmes de 0,02 ; 0,2 ; 20 ; 200 ; 2 000 ?
3°)quels
sont les logarithmes de 0,1 ; 0,2 ; 0,4 ; 0,5 ; 0,8 ?
A l’aide des résultats
de l’exercice précédent
, tracez la courbe qui représente la fonction y = log x pour les valeurs e « x » comprises
entre 0,01 ; et 10.
Echelle des
abscisses :
Echelle des
ordonnées :
Quelle est la racine
carrée de 8 ?
Quel est le logarithme
de cette racine ?
Quelle est la racine
carrée de 10 ?
Quel est sont
logarithme ?
Déduire une valeur
approchée du logarithme de « 3 » ; puis une valeur approchée des
logarithmes de 6 ; 9 ; 12 ; 15 .
Calculer les nombres
dont les logarithmes sont 0, 25 ; 1 ,25 ; 2 ; 25 .
Compléter les phrases suivantes :
1°) les nombres
négatifs n’ont pas de logarithmes.
2°)le logarithme de 1
est égal à 0
3°) les logarithmes des
nombres positifs plus grand que 1 sont positifs.
4°)les logarithmes des
nombres positifs plus petits que 1 sont négatifs ;
5°)seules les puissances de 10 ont pour logarithmes des nombres entiers :
exemple : log 1000 =
3 ; log 0,0001 = - 4
PROPRIETES des
logarithmes.
Théorème 1 :
Le logarithme d’un
produit de facteurs est égal à la somme des logarithmes des facteurs.
Si nous
généralisons : log ( x ![]() y
y![]() z ) = log x + log y + log z
z ) = log x + log y + log z
Théorème 2 : le logarithme d’un quotient est égal
au logarithme du dividende moins le logarithme du diviseur.
On peut donc écrire
que : log ![]() = log D – log d
= log D – log d
Théorème 3 :
Le logarithme d’une puissance d’un nombre
est égal au produit du logarithme de ce nombre par
l’exposant de la puissance.
on peut donc généraliser : log a![]() = n log
a
= n log
a
Théorème 4 : le
logarithme d’une racine d’un
nombre est égal au quotient du logarithme
de ce nombre par l’indice de la racine .
|
|
en généralisant : log
|
|
Physique :