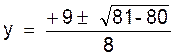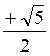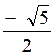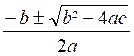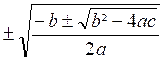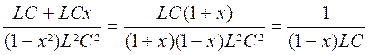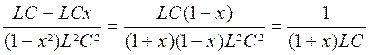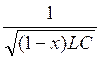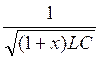Pré requis:

Factoriser - développer
Les I .R .

INFO :

Index : warmaths

Objectif précédent : 1°) Cours résumé : 2°) Résolution d’exercices et de problèmes du second degré INFO : 1°) Suite cours « théorique » 2 °) La Fonction du second degré 3°) La forme canonique.

Objectifs suivants: 1°) Les équations du second degré (présentation) 2°)Le Système d’équations du second degré.

Tableau : 1°)Vers : « second degré » en formation bac prof. 2°) Les équations du second degré (présentation) 3°) Sommaire sur le second degré.

DOSSIER : Résolution des équations BICARREES

1 )	Cours 1 /2
2)	Cours 2 /2

Vocabulaire :

Attention le mot « racine » a deux significations :

1- La ou les « racine(s) » pour désigner «  la ou les solutions » de l’équation .

2- La racine qui désigne que l’on calcule la racine carrée du discriminant.

TEST

COURS

Devoir Contrôle

Devoirs évaluations : - Série 1 - Série 2

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Cours 1 / 2

Définition : N°1 : On appelle ainsi les équations du 4^ème degré qui peuvent se ramener au 2^ème degré , parce qu’elles ne présentent que des puissances paires de l’in connue. Soit résoudre l’équation bicarrée : 4 x ^4 - 9 x² + 5 = 0 On remplacera « x² » par « y » , et on aura l’équation du 2^ème degré : 4 y² - 9 y + 5 = 0 ce qui donnera On aura les réponses : y ‘ = et y’’ = 1 Mais x ² = y ‘ et x² = y ’’ on aura donc : x² = donc et « x » = ce qui donnera les deux valeurs : « x ’ » = et « x ‘’ » = D’autre part on a aussi : x² = 1 Ce qui donnera encore deux autres valeurs : «  x ‘’’ » = + 1 « x ‘’’’ » = - 1 Conclusion : on aura ainsi quatre valeurs pour « x » , ce sera : « x ’ » = ; « x ‘’ » =  ; «  x ‘’’ » = + 1 ; « x ‘’’’ » = - 1 Commentaire : Il peut se faire qu’une des valeurs obtenues pour « y » soit une valeur négative. Dans ce cas, on n’aura que deux solutions ( ou racines ) .

COURS 2/ 2

Cours n°2 :

Définition :

N°2 : On appelle «  équation  bicarrée » une équation du quatrième degré, ne renfermant que des puissances paires de l’inconnue.

Une telle équation peut toujours être « ramenée » à la forme :

(1) a x⁴ + b x² + c = 0

On résout facilement l’équation bicarrée par un changement d’inconnue :

Nous posons : x² = y d’ où x =

L’équation (1) devient :

(2) a y² + b y + c = 0 qui est une équation de second degré en « y »

Dans le cas général , l’ équation (2) donne deux valeurs pour « y »

y =

Soit quatre valeurs pour « x » :

y =

Exemple 1 : x ⁴ - 25 x² + 144 = 0 (1)

d’ où x² = y ; x =

L’équation (1) devient : y ² + 25 y + 144 = 0

Elle admet pour solutions : y’ = + 16 ; y ‘ = + 9

D’ où x₁ = + = +4 ; x₂ = - = - 4 ; x ₃ = + = + 3 ; x ₄ = - = - 3 

Conclusion : l’équation proposée admet quatre solutions.

Exemple 2 : x ⁴ - 12 x² - 64 = 0 (1)

d’ où x² = y ; x =

L’équation (1) devient : y ² - 12 y + 64 = 0

Elle admet pour solutions : y’ = + 16 ; y ‘ = - 4

D’ où x₁ = + = +4 ; x₂ = - = - 4 ;

Et :

x 3 = + x 4 = +

Ces solutions ne sont pas calculables

L’équation proposée n’admet que deux solutions calculables.

Application : ( pour celui qui veut se faire plaisir !!!)

Soit l’équation : ( 1 - x² ) L²É⁴ - 2 ɲ + = 0

Dans laquelle É , L , C , x sont des grandeurs essentiellement positives ; É est l’inconnue, L , C sont connues , « x » est un paramètre.

Posons ɲ = y ; É =

L’équation proposée devient : ( 1 - x² ) L² y ² - 2 y + = 0

Multiplions par C² : ( 1 - x² ) L² C² y ² - 2 L C y + 1 = 0

Identifions les coefficients :

a = (1 - x²) L² C² ; b = - 2 L C ; b’ = LC ; c = + 1

Calcul de ” ‘ : L² C² - ( 1 - x²) L²C² = L²C² - L²C² + L²C²x²

” ‘ = L²C²x²

Calcul de = L C x

y ‘ =

Commentaire : Cette valeur est positive si x < 1

y ‘‘ =

É’ = et É’’ =

Commentaire : Si > 1 seule la valeur de É’’ est positive.

TRAVAUX AUTO FORMATIFS.

CONTROLE :

Que signifie « résoudre » ?

Donner la procédure qui permet de résoudre une équation bicarrée :

EVALUATION:

Résoudre les équations bicarrées :

Série 1

a) 4 x ⁴ - 9 x² + 5 = 0

b) x ⁴ - 25 x² + 144 = 0

c) x ⁴ - 12 x² - 64 = 0

(les corrigés sont dans les cours)

Série 2

1.	x^4 - 12 x² = 25
2.	3 x^4 - 13 x² + 4 = 0
3.	x^4+ 2 x² - 24 = 0
4.	x^4 - 8 x² - 9 = 0

Suite  :

5.	x^4 - 5 x² + 4 = 0
6.	x^4 - 13 x² + 36 = 0