|
|
|
|
Puissances |
|
|
Racines |
|
Objectif précédent
2°)
Signification géométrique de la dérivée. |
aller vers la
liste des cours sur les dérivées. 2° )Etudes de fonctions :
le second degré. |
||
|
|
|
|
|
DOSSIER: Calcul de la dérivée du second degré de la forme : y = a x² + bx + c
|
|
|
Devoir Contrôle |
Devoir
évaluation |
Interdisciplinarité
|
|
Corrigé
Contrôle |
Corrigé
évaluation |
Rappel :
La procédure de calcul des
dérivées découle de la définition
1 ► Donner à la variable un accroissement ∆x ;
2 ► Calculer l’accroissement correspondant ∆y ;
3 ► Ecrire la
rapport 
et simplifier s’il y a
lieu ;
4 ► Chercher la valeur limite de ce rapport
quand ∆x s ‘ évanouit.
Nous savons que
I ) Dérivée d’une constante. ( y = a) ; est : y ‘ = 0
II ) Dérivée de y = a x ; est : y ’
= a
III) Dérivée
de y = x n ; est
: y ’ = n x n-1 ;
IV ) Dérivée de y = ax n ;est
: y’ = an x n-1
Calcul de
la dérivée de y = a x² + b x + c
Première approche :
Question 1 : déterminée la dérivée de la fonction y = 2 x² +
5 x - 4 pour la valeur x = - 2 de la
variable.
La fonction y = 2 x² + 5 x - 4
est définie pour toute valeur de « x ».
|
|
« x » |
« y » |
|
Les 1ère valeurs |
« x0 = - 2 » |
y0 = 8 - 10 - 4 = -
6 |
|
Les 2ème valeurs |
« x1 = - 2 + ∆x » |
y1 = 2 (- 2 + ∆x )²+ 5 (- 2 + ∆x ) - 4 = -6 - 3 ∆x + 2∆x ² |
|
Accroissements |
∆x |
∆y = y 1 - y0
= - 3 ∆x + 2∆x ² |
D’où :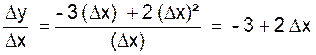 
(
en supposant que ∆x ≠ 0 ).
Quand ∆x tend vers zéro ; 
à pour limite « -3 »
Conclusion :
La dérivée de la fonction y = 2 x² + 5 x - 4
; Pour x = - 2 est
y ‘ = - 3
Deuxième
approche :
Question 2 : Déterminer la dérivée de la fonction y = 2 x² +
5 x - 4 pour la valeur x 0 de la
variable.
La fonction y = 2 x² + 5 x - 4
est définie pour toute valeur de « x ».
|
|
« x » |
« y » |
|
Les 1ère valeurs |
« x0 = - 2 » |
y0 = 2 x0²
+ 5 x0 - 4 |
|
Les 2ème valeurs |
« x1» |
y1 = 2 x1²
+ 5 x1 - 4 |
|
Accroissements |
∆x = x1 - x0 |
∆y = y 1 - y0
= 2 (x1 - x0 )² + 5 (x1 - x0 ) |
Il est plus commode ,
ici , d’utiliser « x1 » , et non « x0+ ∆x) , employé
dans l’exemple précédent , où « x0 »
était numérique.)
D’où :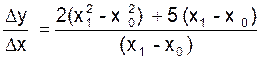 
ou puisque x12 - x 02 = ( x1
- x0 ) ( x1+ x0) :
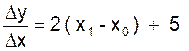( en supposant que ( x1 - x0 ) ≠
0 )
Quand ∆x tend vers zéro ;c’est à dire quand x1 tend vers x0 , alors
à pour limite « 4 x 0 + 5 »
Conclusion :
La dérivée de la fonction y = 2 x² +
5 x - 4 ; Pour x = x0 est « y
’ = 4 x 0 + 5
»
Ceci étant vrai quel que soit x0, on dit que :
« y = 2 x² + 5 x - 4 » a pour dérivée « y ’ =
4 x + 5 »
troisième approche :
Question 3 :
Déterminer la dérivée de la
fonction y = a x² + b x - c
Cette fonction
est définie pour toute valeur de « x ».
|
|
« x » |
« y » |
|
Les 1ère valeurs |
« x0 = » |
y0 = a x0²
+ b x0 + c |
|
Les 2ème valeurs |
« x1» |
y1 = a x1²
+ b x1 + c |
|
Accroissements |
∆x = x1 - x0 |
∆y = y 1 - y0
= a (x1 - x0 )² + b (x1 - x0 ) |
Il est plus commode ,
ici , d’utiliser « x1 » , et non « x0+ ∆x) , employé
dans l’exemple précédent , où « x0 »
était numérique.)
D’où :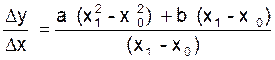 
ou puisque x12 - x 02 = ( x1
- x0 ) ( x1+ x0) :
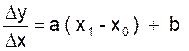( en supposant que ( x1 - x0 ) ≠
0 )
Quand ∆x tend vers zéro ;c’est à dire quand x1 tend vers x0 , alors
à pour limite « 2 a x 0 + b »
Conclusion :
La dérivée de la fonction y = a x² +
b x + c ;
Pour x = x0 est « y
’ = 2 a x 0 + b
»
Ceci étant vrai quel que soit x0, on dit que :
« y = a
x² + b x + c » a
pour dérivée « y ’ =
2 a x + b »
Vérifier que les résultats des deux exemples précédents sont conformes à
cette formule générale.
Exemples :
1°) «
y = 2 x² + 3 x - 5 »
a pour dérivée « y ’ = 4 x
+ 3 »
2°) «
y = 7 x² + 8 x »
a pour dérivée « y ’ = 14 x
+ 8 »
3°) « y = - 5 x² - 9 »
a pour dérivée « y ’ = - 10 x »
Pratiquement, il est commode de dériver un trinôme en remplaçant « x² » par « 2x » , « x » par « 1 » et le terme indépendant par zéro.
Formes particulières :
De la formule générale ; on peut en déduire
les résultats suivants :
1°)
« y = x² » a
pour dérivée « y ’ =
2 x »
2°)
« y = a x² » a pour
dérivée « y ’ = 2 a x »
3°)
« y = x »
a pour dérivée
« y ’ = 1 »
4°)
« y = b x » a pour
dérivée « y ’ = b »
5°)
« y = b x + c » a
pour dérivée « y ’ =
b »
6°)
« y = c » a
pour dérivée « y ’ =
0 »
TRAVAUX AUTO FORMATIFS.
CONTROLE : aucun travail de prévu.
Construction de tangentes
à l’ aide de la dérivée :
1°) y = 
au point « x = -2 )
2°) y =
x² ; y ‘ = 2x au point « x = 1 »
3°) y =
2x² ; y ‘ = 4 x au point « x = 0,5 »
4 °) y = - 0,3 x² ; y ‘ = - 0 ,6 x au point « x = 2 »