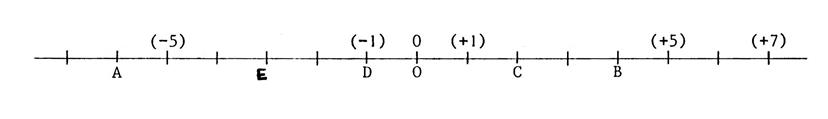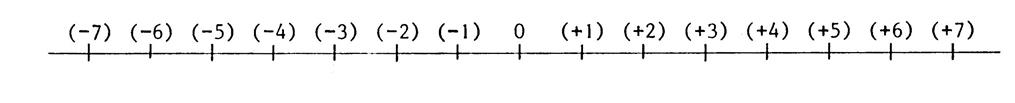fiche de découvertede l' addition avec les nombres décimaux relatifs , corrigé

	1°) Somme de deux entiers relatifs.
	2°) Calculs de sommes d’entiers relatifs.
	3°) Nombres relatifs opposés.
	4 °) Interprétation graphique de l’addition.



		Pré requis : devoir de base
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

1°) Somme de deux entiers relatifs.

Nous prenons comme situation : un commerçant fait ses comptes.

Deux « situations problèmes » se présentent à lui :

· Il reçoit de l’argent ,il aura donc de l’argent « en plus » sur son compte « caisse ».

Exemple : s’il reçoit « 367 € » , il écrira sur sa ligne de compte : « + 367 »

· Il reçoit une facture, il doit effectuer un paiement , il aura donc de l’argent « en moins » sur son compte caisse.

Exemple : s’il paye « 167 € » , il écrira sur sa ligne de compte : « -167 ».

En combinant ces deux possibilités, on peut obtenir les « 6 » situations suivantes :

Activité 1 :

1°) Le commerçant reçoit « 5 € » puis « 13 € »

En définitive , il a reçu ( en €) 5 + 13 = ……18 ….

Ce que l’on traduit en nombres relatifs par : ( + 5 ) + ( + 13 ) = ( + 18 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « + » qui est égale à ……………….)

Remarque : le symbole (signe) opératoire « + » que l’on a utilisé est le même que celui de l’addition des entiers naturels. On l’utilisera dans les cas suivants :

2°) Le commerçant honore ( paie ) deux factures de 5 € et de 11 € . En définitive , il a payé ( en euro ) : 5 + 11 = 16

Ce que l’on traduit en nombres relatifs par : ( - 5 ) + ( - 11 ) = ( - 16 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « - » qui est égale à ………………… .)

3°) Le commerçant reçoit 65 euros , puis paye 27 euros.

En définitive , il a reçu ( en €) 65 – 27 = ……38 ….

Ce que l’on traduit en nombres relatifs par : ( + 65 ) + ( - 27 ) = ( + 38 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « différent » qui est égale à ………………… .)

4°) Le commerçant paie 65 euros , puis en reçoit 27 .

En définitive , il a payé ( en €) 65 – 27 = ……38 ….

Ce que l’on traduit en nombres relatifs par : ( - 65 ) + ( + 27 ) = ( - 38 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « différent » qui est égale à ………………… .)

5°) Le commerçant reçoit 26 euros , puis en paie 67 .

En définitive , il a payé ( en €) 67 – 26 = ……41 ….

Ce que l’on traduit en nombres relatifs par : (+ 26 ) + ( - 67 ) = ( - 41 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « différent » qui est égale à ………………… .)

6°) Le commerçant paie 26 euros , puis en reçoit 67 .

En définitive , il a reçu ( en €) 67 – 26 = ……41 ….

Ce que l’on traduit en nombres relatifs par : (- 26 ) + ( + 67 ) = ( + 41 )

(on dit que l’on a calculé : la somme deux nombres relatifs de signe « différent » qui est égale à ………………… .)

Vocabulaire ( à connaître)

Par exemple : ( + 7 ) + ( - 8 ) = ( - 1 )

( - 1 ) est la somme de ( + 7 ) et de ( - 8 )

( + 7 ) et de ( - 8 ) sont appelés les termes de la somme.

L’opération correspondante s’appelle « l’addition des nombres relatifs »

2°) Calculs de sommes d’entiers relatifs.

Activité 2 : En vous inspirant de ce qui vient d’être fait , calculez.

( + 7 ) + ( - 5 ) = …………( + 2 )….

( + 8 ) + ( - 8 ) = …………0….

( - 5 ) + ( - 8 ) = ……(-13)…….

Activité 3 :

Complétez le tableau ci-dessous :

« + »

( - 4 )

( - 3)

( - 2 )

( - 1 )

( - 0)

( + 1 )

( + 2 )

( + 3 )

( + 4 )

( + 5 )

( + 6 )

( + 7 )

( - 4 )

(- 8)

( - 7 )

( - 6 )

( - 5 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1 )

( + 2 )

( + 3)

( - 3 )

( - 7 )

( - 6 )

( - 5 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( - 2 )

( - 6 )

( - 5 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( - 1 )

( - 5 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( - 0 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 1 )

( - 3 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( +2 )

( - 2 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 3 )

( - 1 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 10)

( + 4 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 10)

( + 11)

( + 5 )

( + 1)

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 10)

( + 11)

( + 12 )

( + 6 )

( + 2 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 10)

( + 11)

( + 12 )

( + 13 )

( + 7 )

( + 3 )

( + 4 )

( + 5)

( + 6)

( + 7)

( + 8)

( + 9)

( + 10)

( + 11)

( + 12 )

( + 13 )

( + 14 )

3°) Nombres relatifs opposés.

Info +++

Sur la droite ci-dessous on a placé deux points situé à « 5 » graduations du point « O ».

Nous avons donc deux valeurs ( - 5 ) et ( + 5 ) , on constate qu’ils sont à l’opposé l’un de l’autre par rapport au point « O ».

On les appellera : les opposés.

· L’opposé de ( +1) est ( - 1)

· L’opposé de ( - 1 ) est ( + 1 )

Activité 4 :

Placez sur la droite deux points « R » et « N » dont la distance à « O » est « 2 » (en graduation)

Ces points ont pour abscisse …(- 2 ) .et …(+ 2 )..Ces nombres sont dits … « opposés »…..

reperage_graduat_3

· ( + 5 ) et ( -5 ) sont opposés. On écrit : ( + 5 ) = Opp (- 5 ) ou ( - 5 ) = Opp ( + 5 )

Activité 4 :

Quel est…………. ?:

L’opposé de ( - 9 ) = ( + 9 )

L’opposé de ( + 5,9 ) = ( - 5,9 )

L’opposé de ( 0 ) = 0

Complétez :

Opp ( + 4 ) = ( - 4 )

Opp ( - 3,6 ) = ( + 3,6 )

Opp ( 0,5 ) = impossible

« 0,5 » n’est pas un relatif..

Calculez : ( + 7 ) + ( - 7 ) = 0 ; ( - 8,4 ) + ( - 8 , 4 ) = 0

Activité 5 :

Sur la droite graduée ci-dessous , placez « A’ » , « E’ », « D’ » , « C’ » et « B’ » les opposés respectifs de « A », « E », « D », « C » et « B ».

rrelatifs_opposes

A retenir :

· L’opposé d’un nombre est obtenu en changeant le signe + en - ou le signe – en + .

· La somme de deux opposés est égale à « 0 ».

4- Interprétation graphique de l’addition.

Nous reprenons le troisième exemple vu dans le cours sur « les nombres relatifs »

Nous tirons au sort des pions « vert » ou « jaune », sue lequel est noté un nombre……

Info : C’est un jeu !!! le pion jaune se déplace sur la droite , le « vert » va sur la gauche……Le premier pion sera posé, au départ, sur la case codée « 0 » .

Tirage n°1 : Nous tirons un jeton « vert » marqué par « 3 » : nous le plaçons sur la case « (- 3 ) » de la bande codée ci-dessous.

Tirage n°2 : Puis nous tirons un pion « 9 jaune » . Celui va déplacer de 9 cases vers la droite , il ira sur la case codée « (+ 6 ) »

( - 6 )

( - 5 )

( - 4 )

( - 3 )

( - 2 )

( - 1 )

( + 1 )

( + 2 )

( + 3 )

( + 4 )

( + 5 )

( + 6 )

( + 7 )

( + 8 )

Ce double déplacement revient au déplacement unique correspondant au tirage du jeton « 6 vert » .

Nota : la couleur du jeton joue le rôle du signe est « + » ou « - » .

Vous retrouvez ainsi l’addition des nombres relatifs. ( …-3..) + ( …+9..) = ( …+ 6 ..)

Au lieu de placer les entiers relatifs dans des cases , nous utilisons une droite graduée.

reperage_002

A l’aide de cette graduation, vous allez déterminer la somme d’entiers relatifs, puis vous vérifiez par le calcul , comme on l’a appris au premier chapitre « somme de deux nombres relatifs »…

Exemple

( - 3 ) + ( + 9)

( - 3 ) + ( + 9) = (+ ( 9- 3)) = ( + 6 )

A partir de « 0 », vous faites un déplacement de « 3 » à gauche, puis de « 9 » à droite……..

- 6

-5

-4

( - 3)

( -2)

(-1)

(-3)

←

( + 9)

→

Activités 6 : On vous demande de faire de même pour les sommes suivantes :

Dessinez les flèches , vérifiez en faisant le calcul et écrire le résultat.

Calcul 2 : ( + 3 ) + ( + 5 )

( + 3 ) + ( + 5 ) = ( + 8 )

- 6

- 5

-4

( - 3)

( -2)

(-1)

+ 8

(+ 3)

→

( + 5)

→

Calcul 3 : ( + 8 ) + ( - 2 )

( + 8 ) + ( - 2 )= ( + ( 8 – 2 )) = ( + 6 )

- 6

-5

-4

( - 3)

( -2)

(-1)

+ 8

(+ 8 )

→

( - 2)

←

( + 6 )

Calcul 3 : ( - 4 ) + ( - 3 )

( - 4 ) + ( - 3 )= ( - ( 4 + 3) ) = ( - 7 )

- 7

- 6

-5

-4

( - 3)

( -2)

(-1)

(- 4 )

←

( - 3)

←

Calcul 4 : (+ 5 ) + ( - 8 )

(+ 5 ) + ( - 8 ) = ( - (8 – 5) ) = ( - 3 )

- 6

-5

-4

( - 3)

( -2)

(-1)

( + 5 )

→

( - 8)

←

Calcul 5 : (- 7 ) + ( + 3 )

(- 7 ) + ( + 3 )= ( - ( 7 – 3) ) = ( - 4 )

( -7 )

- 6

-5

-4

( - 3)

( -2)

(-1)

(-7)

←

( + 3)

→

ACTIVITES « calculs » :


Série 1 :Dans une suite d’addition il est possible d’effectuer les additions dans l’ordre que l’on veut. Calculez de la façon la plus rapide.
A = ( + 9 ) + ( + 8 ) + ( - 3 ) ) + (- 9 )														C = ( - 10 ) + ( + 40 ) + ( - 20 ) + (- 18 )
A = ( + 5 )														C = ( - 8)
B = ( + 5 ) + ( - 9 ) + ( + 10 ) + (- 6 )														D= ( + 28 ) + ( - 85 ) + ( + 82 ) + (- 15 )
B = 0														D = ( + 10 )

Série 2 : Complétez le tableau.
				+				( - 7 )			( + 3 )			( - 5 )			( + 8 )			( + 1 )
				( + 4 )				( - 3 )			( - 1 )			( - 1 )			( + 12 )			( + 3 )
				( - 9 )				( - 16 )			( - 6 )			( - 14 )			( - 1 )			( - 8 )
				( + 16 )				( + 9 )			( + 19 )			( + 11)			( + 24 )			( + 1 7 )
				( - 6 )				( - 13 )			( - 3 )			( - 11 )			( + 2 )			( - 5 )
				( - 8 )				( - 1 5 )			( - 5 )			( - 13)			0			( - 7 )


Série 3 : Complétez le tableau. ( Vous pouvez faire certaines remarques , si on vous autorise à les formuler) !!!!!

		« a »				« b »				« a + b »			Opp ( a + b)		Opp ( a )				Opp (b)			Opp (a ) + opp (b)
		( - 8 )				( + 3 )				( - 5 )			( + 5 )		( + 8 )				( - 3 )			( + 5 )
		( + 4 )				( + 6 )				( + 1 0 )			( - 10 )		( - 4 )				( - 6 )			( - 10 )
		( - 7 )				( - 5 )				( - 12 )			( + 12 )		( + 7 )				( + 5 )			( + 12 )
		( - 2 )				( + 9 )				( + 7 )			( - 7 )		( + 2 )				( - 9 )			( - 7 )

Remarque : Opp ( a + b ) = Opp a + Opp.b

« a »	« b »		« c »		« d »		« a + b »		« (a + b )+ c »			« [ (a + b )+ c] + d »				« c + d »		(a + b )+ ( c + d )			« b + ( c + d) »		« a +[ b + ( c + d)]
( + 6 )	( - 3 )		( + 2 )		( - 7)		( + 3 )		( + 5 )			( - 2 )				( - 5 )		( - 2 )			( - 8 )		( - 2 )
( - 8 )	( + 5 )		( - 4 )		( - 3)		( - 3 )		( - 7 )			( - 10 )				( - 7 )		( - 10 )			( - 2 )		( - 10 )
( + 3 )	( - 7 )		( + 5 )		( + 6)		( - 4 )		( + 1 )			( + 7 )				( + 11)		( + 7 )			( + 4 )		( + 7 )
( - 2 )	( +9 )		( - 5 )		( - 3)		( + 7 )		( + 2 )			( - 1 )				( - 8 )		( - 1 )			( + 1)		( - 1 )

	Wr : Mai 2013