Nov.
2012-11-15
Pré requis:
|
|
|
|
|
|
|
|
ENVIRONNEMENT du
dossier :
|
|
Objectif suivant : 1°) résoudre
une équation du premier degré. 3°) Factoriser ;
développer
ensuite niveau + : plusieurs termes contiennent « x ». |
DOSSIER : LE CALCUL
ALGEBRIQUE :
L’ addition et
La somme en calcul algébrique :
|
|
|
|
|
|
1°)
Addition algébrique |
|
|
|
2°)
Réduction des termes semblables. |
|
|
|
3°) Transformation et calcul : Addition
d’expressions algébriques (polynômes)
pour devenir une somme
algébrique de polynômes entiers en
« x ». (simplification ; ordonnation ; …) |
|
|
|
|
|
|
Devoir Contrôle |
Devoir évaluation |
|
TEST sur le pré requis
vocabulaire :
Vous devez connaître la définition des mots suivants :
« premier
membre , deuxième membre ; terme ; facteur ;
neutraliser ; équation du premier degré »
COURS
|
|
Nous
avons déjà vu comment on indique, par signes,
l'addition, la soustraction, la multiplication division des quantités
algébriques, et c'est l'emploi de ces
signes qui a donné naissance aux expressions littérales que nous avons appelées monômes et polynômes . Mais ces quantités littérales elles-mêmes,
avec leurs signes, leurs lettres, leurs coefficients et leurs exposants sont
soumises à leur tour aux quatre opérations fondamentales, d'après des règles qui constituent le calcul
algébrique. Ces opérations rappellent en général mômes
idées qu'en arithmétique, et comportent mêmes définitions. |
|
|
|
1°)
Addition algébrique |
|
|
|
REGLE : . Pour additionner les
quantités algébriques , il suffit de les écrire les unes à la suite des autres en conservant à chaque terme le signe qui le
précède Soit, par exemple, à ajouter au monôme 3a9
binôme b
— c, on aura pour somme : 3a9 + b - c. Démonstration. En
effet, si à 3a9 on voulait ajouter b ; on écrirait évidemment 3a9 + b
; mais cette somme est plus
grande que celle qu'on demande de toute la
valeur de c: il faut donc en retrancher cette
dernière quantité et poser comme ci-dessus
3 a ² + b - c. Ce
raisonnement, qu'on peut appliquer à tout autre exemple, confirme la règle donnée précédemment. On trouvera donc, d'après cette règle, que la somme des trois polynômes : 7 a b² ; 5 ab² - 2
a ; a m² - n² + 6 n est égale
à : 7 a b² + 5 ab² - 2 a + a
m² - n² + 6 n |
|
|
|
pour mieux
comprendre : il faut le
résultat, il faut transformer les
polynômes en termes algébriques (non simplifiés) et poser lai somme
algébrique : ( revoir : expression et somme
algébrique) 7 a b² devient : ( + 7 a b² ) ; 5 ab² - 2 a devient ( 5 ab²) + ( -
2 a ) ; a m² - n² + 6 n devient ( + a m²) + ( - n²) + ( + 6 n) ensuite faire la
somme : ( +
7 a b² ) + ( 5 ab²) + ( - 2 a ) +( + a m²) + ( - n²) + ( + 6 n) ce qui donne après simplification , l’expression algébrique : 7 a
b² + 5 ab² - 2 a + a
m² - n² + 6 n (voir ci-dessus) |
|
|
|
2°) Réduction des termes semblables.
( revoir : factoriser )
|
|
|
|
Dans une addition
algébrique on rencontre souvent des
termes semblables, et alors il y a lieu d'effectuer l'opération qu'on
appelle réduction,
laquelle consiste à réunir ces termes
semblables en un seul. |
|
|
|
Ainsi, par exemple, 5a2 b + 8 a² b
revient évidemment à 13 a² b De même, le polynôme 7
a b 3 + 10 a
b 3 - 13 a b 3 est égal à
4 a b 3 ( revoir :
factoriser ) Enfin 2 ax – 9 ax +6 ax – ax égale
d'abord 8ax — 10 ax, et se réduit ensuite
à -
2 ax. On
voit, par ces exemples, que la réduction ne porte que
sur les signes et sur les coefficients ; on peut donc
énoncer ainsi la règle Pour opérer la réduction des termes semblables dans un polynôme, il
faut d'un côté
réunir en un seul tous ceux qui sont positifs, de l'autre tous les négatifs,
ensuite retrancher le plus petit coefficient du plus grand numériquement, et donner au reste le signe du plus
grand. Info pratique : Pour éviter toute erreur dans cette
opération, on est dans l'habitude de bâtonner les termes semblables à mesure qu'on les réunit. Remarque
I. L'ordre des termes dans un poly nôme est
indifférent ; ainsi, l'on peut écrire également 8 a² b +
4 b 3 + 2 a 3 – 5 a b²
, ou 2 a3 + 8 a² b – 5 a b² + 4 b 3 ; cependant il vaut mieux
disposer les termes de manière
que les exposants d'une même lettre aillent en croissant
ou en décroissant : c'est ce qu'on appelle ordonner le
polynôme ; quelquefois même c'est indispensable. Le polynôme ci-dessus
écrit de la manière suivante: 2 a3 +
8 a² b – 5 a b² + 4 b 3 , est ordonné par
rapport aux puissances décroissantes de a et d'après les
puissances croissantes de b. |
|
|
|
Remarque II. Au
lieu d'effectuer l'addition de plusieurs polynômes, on se
borne quelquefois à l'indiquer en renfermant chacun d'eux entre deux
parenthèses ( ) ou
entre deux crochets [ ], et en les
réunissant les
uns aux autres par le signe +. Ainsi
l'addition des trois polynômes : « 2a3 — 9b
² » ; « — 7a3 + 5 ab² » ; « 3a3— 8 b3 + 4 » est indiquée comme il suit : ( 2a3
— 9b ² ) + ( — 7a3 + 5 ab² ) + ( 3a3— 8 b3 + 4 ) Remarque III.
Quand on écrit plusieurs polynômes
dont ou veut faire l'addition et qu'ils contiennent des
termes semblables, il est avantageux de les disposer les
uns au-dessous des autres, de manière que les termes
semblables soient dans une même colonne, parce que la
réduction est plus facile; ainsi, pour additionner les
trois polynômes suivants, on les
disposera de la sorte : |
|
|
|
12a3 |
— 9b ² |
|
|
|
|
|
- 7a3 |
+ 5 ab² |
+ b 3 |
|
|
|
|
3a3 |
— 6 a b² |
- 8 b3 |
+ 4 |
|
|
Somme :…. |
8 a3 |
— 10 a b² |
- 7 b3 |
+ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
3°) Addition d’expressions algébriques
(polynômes) pour devenir une somme algébrique de polynômes
entiers en « x ». (simplification ;
ordonnation ; …) |
|
|
|
|
|
|
|
|
|
Les
polynômes donnés sont écrits entre parenthèses ,
à la suite les uns des autres, les parenthèses étant précédées du signe de
l’opération ( addition ou soustraction) à effectuer. |
|
|
|
|
Procédure : 1°)
supprimer les parenthèses. 2°)
Réduire les monômes semblables , en même temps on
réalise l’ordonnation. |
|
|
|
|
Exemple :On donne 3 polynômes : P ; P ‘ ; P ’ ’ |
|
|
|
|
|
P = - 3 x 4 + 8 x² - 5 x
+ 3 P ‘ = 11 x 5 + 14 x 4 - 7 x² + 13 P ‘’ = 15 x 5 - 12 x 3 + 8 x² + 4 x |
|
|
|
3°) On
demande de réaliser A =
P - P ‘ + P ’ ’ |
|
|
|
|
Solution : |
|
|
|
|
A
= ( - 3 x 4 + 8 x² - 5 x + 3 ) -
(11 x 5 + 14 x 4 - 7 x² + 13 ) + (15 x 5 - 12 x 3 + 8 x² + 4 x ) |
|
|
|
|
A
= ( - 3 x 4 ) + ( +
8 x² ) + ( - 5 x ) + (+ 3 ) + ( - 11 x 5 ) + ( -14 x 4 ) + ( + 7 x² )+ ( -13
) +
(15 x 5 )+ ( - 12 x 3 ) + ( + 8 x² ) + (+ 4 x ) |
|
|
|
|
On réduit
et on ordonne ( ce
sont des opérations simultanées) : |
|
|
|
|
A =
( + 4 x 5 ) + ( - 17
x 4 ) + ( - 12 x 3
) + ( + 23 x² ) + ( - x ) + ( – 10 ) |
|
|
|
|
La somme algébrique , peut
se transformer en expression
algébrique : A = + 4 x 5 - 17 x 4 - 12 x 3 + 23 x² - x – 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CONTROLE:
|
|
1°) Additionner les polynômes (7 a — 6b) et (5 a² - b 3 + c) |
|
|
|
R ; = 7 a — 6b + 5 a² - b 3 + c ;……………..(on ne demande pas
d’ordonner) |
|
|
|
2°) Ajouter 13 am2 - 9a² m + a 3 avec
7a 2 m .+ 5 am3 — a 3 b. |
|
|
|
R : 13 am2 + a 3 +
5 am3 — a 3
b - 2 a² m |
|
|
|
3°) Faire la somme des trois polynômes
suivants : |
|
|
- 4 a b3 |
+ 6 a² b² |
- 15 a 3 b |
+ 9 a 4 |
|
|
7a b 3 |
- 11 a² b² |
- 9 a 3 b |
|
|
|
- a
b 3 |
+ 8 a² b² |
+ 22 a 3 b |
|
+ 9 |
|
+ 2 a b3 |
+ 3 a² b² |
- 2 a 3 b |
+ 9 a 4 |
+ 9 |
|
|
4°)
Ajouter les polynômes . |
|
|
8 a² |
|
- 2 b² |
|
|
|
- a² |
|
+ 7 c² |
+2 |
|
|
ab |
+ 2 b² |
+4c² |
|
|
|
|
|
|
|
|
Corrigé :
|
8 a² |
|
- 2 b² |
|
|
|
- a² |
|
|
+ 7 c² |
+2 |
|
|
ab |
+ 2 b² |
+4c² |
|
|
7 a² |
|
+ 0 b² |
+ 11 c² |
** |
* 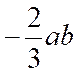 +
+
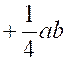 +
ab = ab ( -
+
ab = ab ( - ![]() +
+ ![]() + 1 ) =
a b (
+ 1 ) =
a b ( 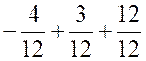 ) =
) = 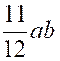
** ![]() +2
+2 ![]() =
= 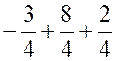 =
= ![]()
|
|
4°) Additionner : a + |
|
|
|
R = 2a |
|
|
|
5° ) Trouver une
expression qui surpasse « a »
d'autant d'unités qu'il y en « a » dans « b » |
|
|
|
E = a + b – a ( ?) |
|
|
|
6°) On
met dans une bourse d'abord une somme « n », ensuite une autre somme « b » , et plus tard on en retire
une somme « c » ; que reste-t-il
dans la bourse? |
|
|
|
«reste = n + b – c » |
|
|
|
7°) En
désignant par « x » l'âge d'une personne, on demande d'exprimer l'âge qu'elle aura dans 15 ans. |
|
|
|
Age = x + 15 |
|
|
|
8°) On
achète de l'étoffe pour « a » euros
une premiers fois, et l'on
renouvelle ensuite la même dépense pendant quatre fois encore
; on demande d'exprimer la somme totale dépensée |
|
|
|
R = a + 4 a =
5 a |
|
|
|
9°) Le grand côté d'un rectangle surpasse de
« a » mètres le plus petit en représentant par « x » ce petit côté ; quelle est l'expression
du contour de ce rectangle ? |
|
|
|
P = 2x + 2 ( x+ a ) |
|
TRAVAUX AUTO FORMATIFS.
CONTROLE:
EVALUATION:
|
|
1°) Additionner les polynômes (7 a — 6b) et (5 a² - b 3 + c) |
|
|
|
R ; = 7 a — 6b + 5 a² - b 3 + c ;……………..(on ne demande pas
d’ordonner) |
|
|
|
2°) Ajouter 13 am2 - 9a² m + a 3 avec
7a 2 m .+ 5 am3 — a 3 b. |
|
|
|
R : 13 am2 + a 3 +
5 am3 — a 3
b - 2 a² m |
|
|
|
3°) Faire la somme des trois polynômes suivants
: |
|
|
- 4 a b3 |
+ 6 a² b² |
- 15 a 3 b |
+ 9 a 4 |
|
|
7a b 3 |
- 11 a² b² |
- 9 a 3 b |
|
|
|
- a
b 3 |
+ 8 a² b² |
+ 22 a 3 b |
|
+ 9 |
|
+ 2 a b3 |
+ 3 a² b² |
- 2 a 3 b |
+ 9 a 4 |
+ 9 |
|
|
4°)
Ajouter les polynômes . |
|
|
8 a² |
|
- 2 b² |
|
|
|
- a² |
|
+ 7 c² |
+2 |
|
|
ab |
+ 2 b² |
+4c² |
|
|
|
|
|
|
|
|
Corrigé :
|
8 a² |
|
- 2 b² |
|
|
|
- a² |
|
|
+ 7 c² |
+2 |
|
|
ab |
+ 2 b² |
+4c² |
|
|
7 a² |
|
+ 0 b² |
+ 11 c² |
** |
* 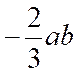 +
+
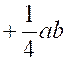 +
ab = ab ( -
+
ab = ab ( - ![]() +
+ ![]() + 1 ) =
a b (
+ 1 ) =
a b ( 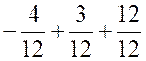 ) =
) = 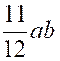
** ![]() +2
+2 ![]() =
= 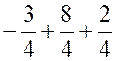 =
= ![]()
|
|
4°) Additionner : a + |
|
|
|
R = 2a |
|
|
|
5° ) Trouver une
expression qui surpasse « a »
d'autant d'unités qu'il y en « a » dans « b » |
|
|
|
E = a + b – a ( ?) |
|
|
|
6°) On
met dans une bourse d'abord une somme « n », ensuite une autre somme « b » , et plus tard on en retire
une somme « c » ; que reste-t-il
dans la bourse? |
|
|
|
«reste = n + b – c » |
|
|
|
7°) En
désignant par « x » l'âge d'une personne, on demande d'exprimer l'âge qu'elle aura dans 15 ans. |
|
|
|
Age = x + 15 |
|
|
|
8°) On
achète de l'étoffe pour « a » euros
une premiers fois, et l'on
renouvelle ensuite la même dépense pendant quatre fois encore
; on demande d'exprimer la somme totale dépensée |
|
|
|
R = a + 4 a =
5 a |
|
|
|
9°) Le grand côté d'un rectangle surpasse de
« a » mètres le plus petit en représentant par « x » ce petit côté ; quelle est l'expression
du contour de ce rectangle ? |
|
|
|
P = 2x + 2 ( x+ a ) |
|