|
|
4ème
collège |
||
|
|
|||
|
|
Vers le corrigé ( le lien n’est pas activé) |
||
|
Pré requis: |
|
ENVIRONNEMENT du
dossier:
|
Objectif précédent :: 1°) le rectangle activités découvertes.
2°) Voir travaux classe 6ème :rectangle et propriétés. |
1.
Le rectangle ce qu’il faut savoir et retenir. 2.
Le losange 3.
le carré 4.
|
2.
Liste
des cours de géométrie.. 3.
Fiches activités de géométrie (à
consulter) |
DOSSIER : LE RECTANGLE en 4ème
|
|
Fiche 1
: le rectangle. (définition , propriétés ,…) |
|
|
|
Fiche 2 : Comment reconnaître qu’un
quadrilatère est rectangle ? |
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
Le rectangle |
|
||
|
|
Définition : On appelle
« rectangle » tout parallélogramme ayant un angle « droit ».
|
|
||
|
|
Puisqu’un rectangle est d’abord un parallélogramme , alors il possède toutes les propriétés
du parallélogramme. Il en possède d’autres (
étudiées en 6ème et 5ème ). Nous allons les récapituler ci-dessous. |
|
||
|
|
Propriété 28 : Si un quadrilatère est un rectangle alors ses côtés
consécutifs sont perpendiculaires . |
|
||
|
|
Ce qui revient à dire : ses 4 angles sont
des angles droits. |
|
||
|
|
|
|
||
|
|
Propriété 29 : Si un quadrilatère est un rectangle alors il
possède deux axes de symétrie qui sont les médiatrices des côtés opposés. |
|
||
|
|
Activité : Tracez ces axes sur la figure ci-dessus. |
|
||
|
|
|
|
||
|
|
Propriété 30 : Si un quadrilatère est un rectangle alors ses
diagonales se coupent en leur milieu
. |
|
||
|
|
|
|
||
|
|
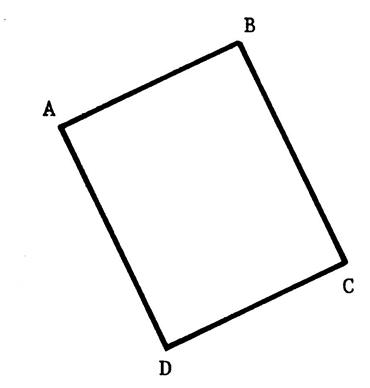
Activité 1 : Considérons le rectangle « ABCD »
ci-contre. Puisque tout rectangle est un parallélogramme , alors grâce à la propriété n°8 ,
ses diagonales se coupent en leur milieu . Soit « O » ce point . D’après la propriété « 30 » , les
diagonales ont même mesure donc « OA = OB = OC = OD ». Donc les 4
points « A » , « B »,
« C » , « D » sont situés sur le cercle de centre « O ». Activité : Tracez ce cercle sur la figure. |
|
|
|
|
|
Théorème 4 . Si un quadrilatère est un rectangle
, alors ses sommets sont situés sur un cercle. Le centre de ce cercle est le centre du
rectangle. |
|
||
|
|
|
|
||
|
|
On dit que le rectangle est inscrit
dans le cercle. Le cercle est appelé « cercle circonscrit »
au rectangle. |
|
||
|
|
|
|
||
|
|
Activité n° 2 … Dites en
l’expliquant si la réciproque de ce théorème est vraie. Illustrez votre réponse en complétant le dessin
ci-contre. |
|
|
|
|
|
|
|
||
|
|
Activité n° 3 « EFG » est un triangle rectangle en
« F ». « H » , « I » , «J » sont les milieux respectifs de
[ FG ] ,
[GE ] , [EF]. Démontrez que « FHIJ » est un rectangle . |
|
||
|
|
|
|
||
|
|
Activité n° 4 « KLM » est un triangle rectangle en
« L ». « N » est un point de [ KM ] On trace par « N » la parallèle à ( LM ) qui coupe ( L K ) en « P ». On trace par « N » la parallèle à ( LK ) qui coupe ( L M ) en « R ». Démontrez que « LN = PR ». |
|
||
|
|
Fiche 2 : Comment reconnaître qu’un
quadrilatère est rectangle ? |
|
|
|
|
La première façon de reconnaître un rectangle
c’est partir de sa définition. Mais voici une autre façon que vous avez étudiez
dans les niveaux précédents : |
|
|
|
|
Propriété 29 : Si un quadrilatère a
ses côtés consécutifs perpendiculaires alors ce quadrilatère est un
rectangle. |
|
|
|
|
|
|
|
|
|
On peut dire aussi que
«si un quadrilatère a 3 angles droits alors c’est un rectangle ». (vous pouvez expliquer pourquoi (verbalement) il
suffit de trois angles droits.) |
|
|
|
|
|
|
|
|
|
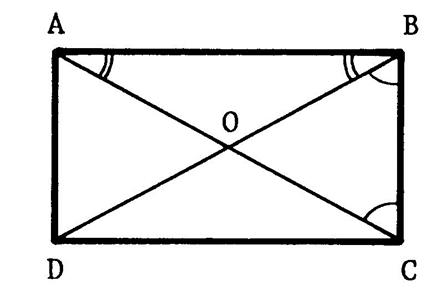
Activité n°1 « ABCD » est un parallélogramme de
centre « O ». Ses diagonales [ AC
] et [ BD ] ont même longueur. Nous devons prouver que « ABCD » est un ..rectangle.. Hypothèse -
…………. -
…………………………………………….. Conclusion : |
|
|
|
|
Démonstration : Puisque « ABCD » est un
parallélogramme, alors grâce à la propriété n°8 : « O » est le
milieu de [ AC ]
et de [ BD ]. Et comme par hypothèse ,
« AC = BD » alors « OA
= OB
=
OC =
OD » . Donc , par définition , « AOB » et « BOC » sont des
triangles isocèles. Donc , d’après la propriété « 24 » , Dans le triangle « ABC », la somme des
angles est égale à 180° ( propriété
6) Donc : , En tenant
compte des deux égalités précédentes , on peut
écrire : 2 Et comme par hypothèse ,
« ABCD » est un parallélogramme , alors grâce à la …………………………………………………,
« ABCD » est un …………………………………….. |
|
|
|
|
Théorème 5 : Si un parallélogramme a ses diagonales de même longueur
alors ce parallélogramme est un rectangle. |
|
|
|
|
|
|
|
|
|
Autre façon : Si dans un quadrilatère les diagonales ont même
longueur et se coupent en leur milieu alors ce quadrilatère est un rectangle. |
|
|
|
|
|
|
|
|
|
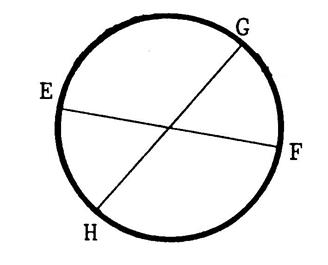
Activité n°2 [ EF] et [ GH ] sont deux diamètre du cercle . Démontrez que
« EGFH » est un rectangle. |
|
|
|
|
|
|
|
|
|
Activité n°3 « ABCD » est parallélogramme. -
La bissectrice de -
La bissectrice de 1°) Démontrez que 2°) Démontrez que « EFGH » est un
rectangle. |
|
|
|
|
|
|
|
|
|
Fait le 9 oct.2014 |
|
|
|
|
|
|
||||||||||||||
|
|
CONTROLE : Quelles sont les caractéristiques ( propriétés ) du rectangle ? EVALUATION Tracer :
|
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|