Pré requis:
|
Nomenclature 1 |
|
|
Informations |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : 1.
Somme des angles dans un triangle 2.
Fiches activités sur la somme des angles dans un triangle. |
Objectif suivant |
Info sur les triangles . |
DOSSIER : Les triangles particuliers
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
Ils sont au nombre de trois .
Ces triangles particuliers sont :
|
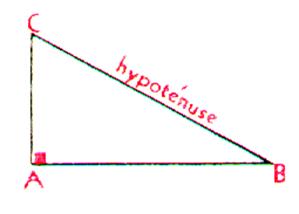
Le triangle rectangle |
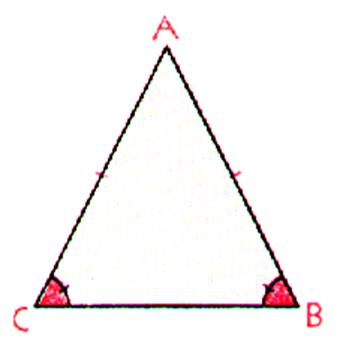
le triangle isocèle |
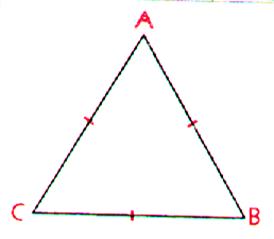
le triangle équilatéral |
|
Angles : Un des trois angles a
une valeur de 90° ,
appelé "angle droit" Cotés : Les trois cotés sont
de longueur différente. Avec un cas particulier :2 cotés peuvent avoir la même longueur , nous sommes en présence du demi carré . (le plus
grand coté étant la diagonale du carré )que l ' on peut définir comme étant le triangle
rectangle isocèle |
|
|
Angles : si l’on connaît l’angle au sommet ( en
A ) on détermine la valeur de l’angle
C et l’angle B . Ils sont égaux : Calcul : 180° - angle A =
somme( angle C + angle B ) L’angle C = l’angle B = Somme ( angle C +
angle B) : 2
Exemple : si l’angle A = 38 ° ; on calcule
successivement : 180 ° - 38 ° = 142° ; 142° : 2 =
71° ; Conclusion : l’angle C et l’angle B sont égaux et ils
valent respectivement 71° Côtés : Un triangle isocèle est un triangle dont
deux des cotés sont de même dimension
ou de même longueur. Avec un cas particulier : le triangle rectangle isocèle 2 cotés ont la même longueur ,et
un angle mesure 90° ; nous sommes en présence du demi carré . (le plus
grand coté étant la diagonale du carré ) |
|
|
Un triangle équilatéral est un
triangle dont ses trois cotés sont de
même dimension ou de même longueur. ses trois angles sont égaux ( de même mesure angulaire : 60° ) 180 ° : 3 = 60° |
|
Travaux auto- formatifs.
CONTROLE:
1° ) Combien de droites faut il pour construire un triangle. ?
2° ) Compléter la phrase suivante :Un
triangle est le nom donné à une surface
ayant …… angles et ……… cotés.
3°) Comment nomme t on le triangle
quelconque ?
4°) Citer les trois triangles particuliers.
5°)Quelles sont les caractéristiques du triangle rectangle ?
6°)Quelles sont les caractéristiques du triangle isocèle?
7°)Quelles
sont les caractéristiques du triangle
équilatéral?
|
Sujet
complet |
|
Consignes
: A
faire sur feuille format A3 sans quadrillage., attention à la mise en
page!
I ) Tracer un triangle quelconque:
AB = 130mm (le plus
long coté)
L'angle A vaut 40°
L'angle B vaut 65°
II
)
Tracer un triangle rectangle en B dont un angle vaut 35° et l'hypoténuse =130mm
III
)Tracer un triangle isocèle:
un angle au sommet
vaut 83°
longueur des cotés égaux = 90
mm
IV) tracer un triangle équilatéral
dont la longueur des cotés
= 90 mm