WARMATHS

La translation

Propriétés conservées par la translation.

Définitions:

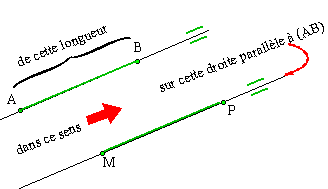
Une translation qui transforme le point A en le point B est un déplacement rectiligne dans le plan (glissement) qui amène le point A sur le point B.

Le point B est appelé translaté de A dans cette translation. Nous dirons aussi que B est l'image de A dans cette translation.

Pour définir une translation il faut donc connaître deux points: un point de départ (A) et un point d'arrivée (B). Nous définissons ainsi trois choses:

- une droite (AB) sur laquelle nous nous déplaçons (le déplacement est rectiligne).

- une distance AB. C'est la longueur du parcours, du glissement.

- un sens de parcours: de A vers B. Aller dans le sens inverse (de B vers A) c'est utiliser une autre translation (la translation inverse, celle qui nous ramène à notre point de départ).

Tous les points du plan peuvent alors être transformés de la même manière que A se transforme en B. Il suffit, pour translater un point M en P dans la translation qui transforme A en B, de:

- suivre un chemin parallèle à la droite (AB): donc (MP) doit être parallèle à (AB)

- parcourir la même distance: donc MP doit être égal à AB.

- se déplacer sur (MP) dans le même sens que sur (AB).

Propriétés fondamentale:

Dans le paragraphe précédent nous avons vu que translater M en P dans la translation qui transforme A en B, c'est construire un point P tel que : MP= AB et la droite (MP) soit parallèle à la droite (AB) en respectant le sens du déplacement.

Comme le quadrilatère ABPM est non croisé avec AB=MP et (AB) parallèle à (MP)

alors ABPM est un parallélogramme.

Nous avons donc le théorème:

Dans la translation qui transforme A en B:

Si M a pour translaté P

Alors ABPM est un parallélogramme.

Remarque:

Si M est sur la droite (AB) (ou :M aligné avec A et B) alors P est aussi sur (AB) et le parallélogramme n'a plus de hauteur (qui est l'écartement entre les deux droites (AB) et (MP)). Nous dirons qu'il est "aplati".

Construction du translaté d'un point:

Soit les points A et B. Nous allons construire l'image du point M dans la translation de A vers B.

Cas particulier: le point M est sur la droite (AB).

Lorsque A va en B, M va en P. Ces quatre points sont alignés.

Le parallélogramme ABPM est dit aplati.

Cas général:

Il y a plusieurs façons de procéder: tout dépend des données connues et du matériel disponible.

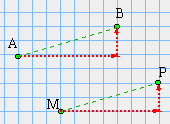
- Sur papier quadrillé: Nous connaissons les points A, B et M. Nous devons construire le point P translaté de M dans la translation qui transforme A en B.

Les constructions ci-dessous ne sont envisageables que si les points A, B et M sont sur des noeuds (intersections) du quadrillage.

Le modèle de translation est donné par les positions des points A et B. Nous comptons le nombre de carreaux qui séparent ces deux points. D'abord horizontalement, puis verticalement. Voici deux exemples:

De A à B:

Horizontalement: 7 carreaux à droite

Verticalement: 2 carreaux vers le haut

De A à B:

Horizontalement: 4 carreaux à gauche

Verticalement: 7 carreaux vers le bas

Puis nous effectuons le même comptage, dans le même ordre (horizontalement puis verticalement) à partir du point M. Nous obtenons le point P.

- en construisant un parallélogramme:

Dans la translation de A vers B, si le point P est le translaté de M alors ABPM est un parallélogramme. Il nous faut donc construire un parallélogramme dont nous connaissons trois sommets: A, B et M. Le quatrième sommet sera P.

Il y a deux manières de procéder: soit en utilisant l'égalité des côtés opposés d'un parallélogramme (méthode 1), soit en utilisant le centre du parallélogramme comme centre de symétrie (méthode 2).

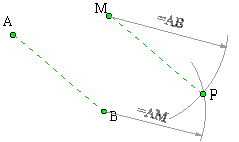
Méthode 1:

Tracez, avec M comme centre, un arc de cercle de rayon égal à AB.

Tracez, avec B comme centre, un arc de cercle de rayon égal à AM.

Soit P l'intersection de ces deux arcs. Comme MP=AB et BP=AM alors ABPM est un parallélogramme.

Le point P est donc le translaté de M dans la translation de A vers B.

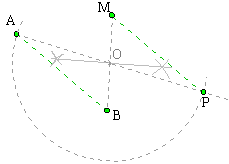
Méthode 2:

Tracez le segment [MB]. C'est une diagonale du parallélogramme ABPM. Soit O son milieu (pour déterminer avec précision ce milieu, il est nécessaire de tracer la médiatrice de [MB]).

Tracez la droite (AO). Coupez le prolongement de (AO) vers O, par un arc de cercle de centre O et de rayon OA. Soit P le point obtenu (P est le symétrique de A par rapport à O). Comme [AP] et [BM] se coupent en leur milieu O alors ABPM est un parallélogramme.

Le point P est donc le translaté de M dans la translation de A vers B.

Translatées de quelques figures simples:

Les constructions suivantes reposent sur la construction du translaté d'un point. Nous utiliserons de préférence la méthode 1 décrite dans le paragraphe précédent (la méthode 2 convient aussi, bien sûr, mais elle induit trop de constructions ce qui nuit à la clarté des figures).

Pour toutes les constructions ci-dessous, la translation utilisée est celle qui transforme A en B.

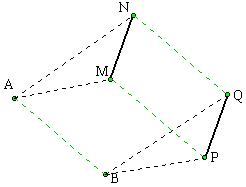
translaté d'un segment:

Le segment [MN] a deux points remarquables: ses extrémités M et N. Pour translater ce segment il suffit de translater ses extrémités et de joindre les deux points obtenus.

Le translaté d'un segment est un segment parallèle de même longueur.

Remarque: Nous avons deux parallélogrammes ABPM et ABQN avec un côté commun [AB]. Nous avons donc: AB=MP=NQ et (MP) et (NQ) parallèles à (AB) . Comme MNQP est un quadrilatère non croisé qui a deux côtés parallèles et de même longueur alors MNQP est un parallélogramme.

Comme MNQP est un parallélogramme alors [MN] et [QP] ont même longueur et sont parallèles.

translatée d'une droite:

Il suffit de choisir deux points M et N sur la droite (D) et de les translater en P et Q. La droite (PQ) est l'image de la droite (D) dans la translation de A vers B..

Le translaté d'une droite est une droite qui lui est parallèle.

Pratiquement:

Pour translater une droite il suffit donc de choisir un point M sur cette droite, de le translater en un point P et de tracer par P une droite parallèle à la droite donnée.

Remarque: si la droite (D) est parallèle à la droite (AB) alors la droite (D) glisse sur elle même dans le mouvement de translation de A ver B. L'image de (D) est donc (D). Nous dirons qu'elle est globalement invariante.

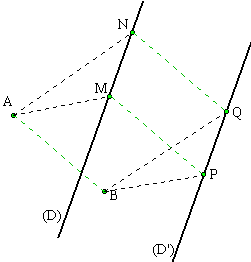
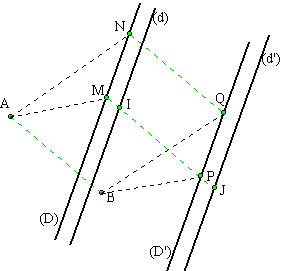
translatées de deux droites parallèles:

Les droites (D) et (d) sont parallèles. Nous construisons d'abord l'image de (D) comme ci-dessus. Nous obtenons (D'). Nous pourrions construire l'image de (d) de la même façon mais nous préférons, afin de ne pas encombrer la figure, construire l'image de I, intersection de (MP) avec (d). Soit J l'image de I (remarquez que PJ=MI). Par J nous traçons (d') parallèlement à (D').

Il est facile de montrer que les quatre droites (D), (d), (D') et (d') sont parallèles entre elles.

Les translatées de deux droites parallèles sont deux droites parallèles entre elles et parallèles aux deux droites données.

Pratiquement:

Nous translatons la droite (D) en choisissant un point M dessus et en le translatant en un point P par lequel nous traçons une droite parallèle (D') à (D). La construction de P nous permet de choisir le point I sur la droite (d) et de le translater en le point J par lequel nous traçons la droite (d') parallèle à (D').

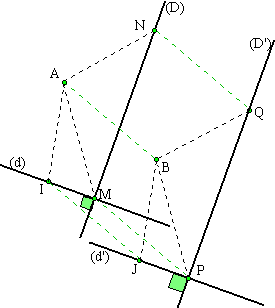
translatées de deux droites perpendiculaires:

Les droites (D) et (d) sont perpendiculaires en M. Soit N un point de (D) et I un point de (d). Il suffit de construire les images P, Q et J de ces trois points puis de tracer les droites (PQ) et (PJ). Nous avons (PQ) parallèle à (D) et (PJ) parallèle à (d). Nous avons donc un parallélogramme avec un angle droit en M. Ce parallélogramme est donc un rectangle. Ce qui démontre qu'il y a un angle droit en P et que les droites images sont perpendiculaires comme les deux droites données.

Les translatées de deux droites perpendiculaires sont deux droites perpendiculaires entre elles et parallèles deux à deux aux deux droites données.

Pratiquement:

Il suffit de translater trois points: le point d'intersection des deux droites perpendiculaires, un point choisi sur l'une et un autre point choisi sur l'autre. Par les images de ces points nous traçons des droites parallèles aux deux droites données.

ou encore

Nous translatons (D) en (D') à l'aide des translatés Q et P de N et M point d'intersection avec (d). En P nous traçons la droite perpendiculaire à (D'): nous obtenons (d').

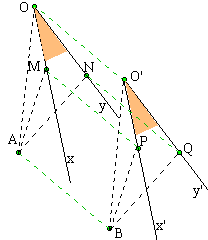
translaté d'un angle:

Soit l'angle de sommet O et de côtés [Ox) et [Oy). Nous choisissons un point sur chacun des côtés: M et N. Les images O', P et Q des points O, M et N sont construites de la façon habituelle. Les demi-droites [O'P) et [O'Q) sont les côtés de l'angle image. Nous démontrons en cours que la mesure de l'angle image est égale à la mesure de l'angle donné (sur la figure ci-dessous: prolongez [Oy) qui coupe [O'x') en I puis démontrez que les angles xÔI, OÎO' et IÔ'y' ont même mesure en utilisant le théorème des droites parallèles coupées par une sécante).

Le translaté d'un angle est un angle de même mesure et dont les côtés sont parallèles deux à deux aux côtés de l'angle donné.

Pratiquement:

Il suffit de translater trois points: le sommet de l'angle, un point choisi sur l'un des côtés et un autre point choisi sur l'autre côté. Par les images de ces points nous traçons des demi-droites parallèles aux deux demi-droites données.

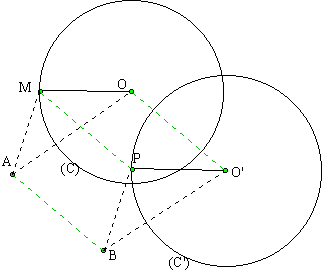
translaté d'un cercle:

Soit le cercle de centre O et de rayon OM. Nous translatons le rayon [OM]. Nous obtenons le segment [O'P] de même longueur (voir translaté d'un segment). Tous les rayons du cercle de centre O ont la même longueur. Par translation tous ces rayons sont translatés en des segment de même longueur d'extrémité O'. L'image du cercle de centre O est donc un cercle de centre O' et de rayon O'P (égale à OM)

Le translaté d'un cercle est un cercle de même rayon et dont le centre est le point translaté du centre du cercle donné.

Pratiquement:

Le cercle image a le même rayon que le cercle donné. Il suffit donc de translater le centre du cercle donné et avec ce point comme centre nous traçons le cercle image en utilisant un rayon égal au rayon du cercle donné.

Propriétés conservées par la translation:

Le paragraphe précédent illustre les propriétés suivantes:

Les translations conservent:

Les distances.

Le parallélisme et l'orthogonalité.

Les mesures des angles et les alignements.

Les aires: le calcul sur les aires utilise des longueurs et des propriétés (angles notamment) qui sont conservées.


[Accueil]	[Répertoire]	[Haut de page]