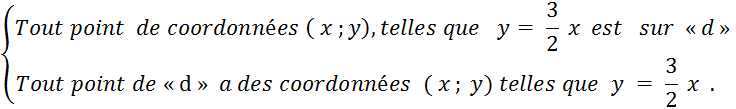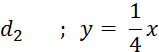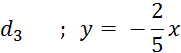Classe de 3^ème
	Vers le corrigé

Info pédagogique : cours niveau V

Ce cours est à maîtriser entièrement par les élèves Bac prof. :

1°) il faut savoir tracer une droite à partir d’un point donné et connaissant la pente de cette droite.

2°) savoir tracer la droite tangente en un point d’une courbe et connaissant sa dérivée en ce point.

Pré requis:

Droites et repérage

Les repère cartésiens

ENVIRONNEMENT du dossier:

Index

AVANT : Equation de droite . 2°) « Pente »

COURS

APRES : 1°) Les droites croissante ; décroissante,.. 2°)le parallélisme et la perpendicularité 3°) recherche de l'équation d'une droite .

Complément d’Info : Liste des objectifs de cours Fonction affine (présentation) Liste des cours d’algèbre

Classe de 3^ème

TITRE : Fiches sur LES EQUATIONS DE DROITES dans un repère.

Fiche n°1 : Droite passant par l’origine du repère. Equation de la forme «  y = mx »

Voir la suite : Droite ne passant pas par l’origine du repère : équation de la forme : y = mx + p

Travaux ; devoirs			Corrigé
TEST	Contrôle	évaluation	Contrôle	évaluation

Interdisciplinarités : (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

Fiche n°1 : Droite passant par l’origine du repère.
Rappel :
Etant donné un nombre «  » , on appelle « application linéaire » de coefficient «  » le procédé qui a tout nombre «  » faire correspondre «  ». Dire que «   » par cette application linéaire c’est dire que «   » La représentation graphique d’une application linéaire de coefficient « m » est la droite passant par l’origine du repère et le point de coordonnées «  ( ) ».
Exemple : Considérons l’application linéaire de coefficient : «  » désignant un nombre quelconque et «  » son image , . Complétez le tableau ci-dessous :
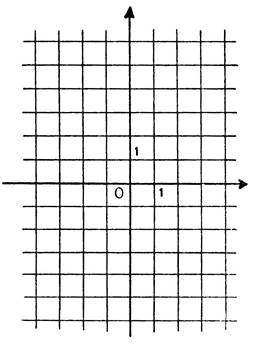
Sur la figure ci-contre placez les 7 points dont les coordonnés sont dans le tableau ci-dessus. Tracez la droite par les points que vous avez placés. Nous appelons «  » cette droite. On dira que : «  «  » est la représentation graphique de l’application linéaire » Ce qui signifie que :
· D’après ce que l’on vient de rappeler , on peut dire dans le cas général :
Le théorème suivant : Dans le plan muni d’un repère, l’ensemble des points dont les coordonnées ( ) vérifient une relation de la forme « » ( « » étant un nombre déterminé ) est (a pour forme ) une droite passant par l’origine du repère. «  » est appelé « coefficient directeur » de la droite.
Inversement : Dans un plan muni d’un repère, étant donné une droite quelconque passant par l’origine du repère, existe-t-il toujours une relation de la forme «  y = mx » liant les coordonnées ( x ; y ) de chacun des points de la droite ?
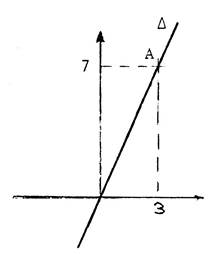
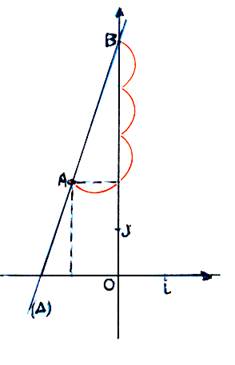
Voir ci-contre ;la figure : Prenons par exemple la droite « Δ » passant par l’origine et le point «   ». Cherchons si les coordonnées ( ) des points de « Δ » qui vérifient une relation de la forme « »
On place un point sur « Δ » ( exemple « A » ), on relève ses coordonnées. Pour le point « A » son abscisse «  » et son ordonnée «   » sont telles que «  » ( Vérifiez-le )
En effet : Dans l’équation « » on remplace les lettres : et  ; on obtient l’égalité : ou « » ; en transformant l’égalité on obtient :  ; On remplace la valeur de « m » trouvée dans l’égalité « » pour obtenir : « »
Or d’après le théorème précédent , l’ensemble des points du plan , donc les coordonnées ( x ;y ) vérifient l’égalité «  » est une droite passant par l’origine. Puisqu’elle passe aussi par « A » , elle est confondue avec « Δ » , donc tous les points de « Δ » ont des coordonnées ( x ; y) qui vérifient la relation «  » et sont les seuls à vérifier. L’écriture «  » est appelée « équation de la droite « Δ » ». et «  » est le coefficient directeur.
Cas général :					Info ++@ ….
Ce que l’on vient de faire pour « Δ »  , on peut le faire dans le cas général. A part l’axe des ordonnées pour lequel tous les points ont pour abscisses « 0 », pour toute droite passant par l’origine , il est possible de trouver un nombre « m » tel que les coordonnées ( x ; y ) de tous les points de la droite vérifient une relation de la forme « » . On dira alors :
Définition : Dans le plan muni d’un repère, on appelle « équation de droite » toute relation vérifiée par les coordonnées ( x ; y) des points de la droite et par eux seulement.
Théorème : Dans un plan muni d’un repère , toute droite passant par l’origine du repère ( autre que l’axe des ordonnées ) a une équation de la forme « » .
Remarque 1 : «  » est vérifiée par les coordonnées de tous les points de « Δ » et par eux seulement . Ce qui est vrai pour «  »  l’est aussi pour «  » ou «  » ou «  » ou «  » ; etc. ….On les appelle aussi équations de la droite « Δ » ; mais il n’y a qu’une seule de la forme « » C’est  « » quand on dit « l’équation d’une droite » on sous-entend « équation de la forme « » ».
Remarque 2 : Tous les points de l’axe des ordonnées ont pour abscisse : 0 L’axe des ordonnées a pour équation « x = 0 » . Il n’a pas d’équation de la forme « » . Tous les points de l’axe des abscisses ont pour ordonnée : 0 L’axe des abscisses a pour équation « y = 0 » . Il n’a pas d’équation de la forme « » ; avec « m = 0 » .
Recherche de l’équation de droites passant par l’origine.
Dans le plan muni d’un repère, déterminons l’équation de la droite passant par l’origine et le point « A ( 4 ; 5 ) »
Puisque la droite passe par l’origine ( point « O (0 ;0)») , son équation est de la forme «  y = m x » « A » étant un point de la droite , ses coordonnées « ( 4 ; 5 ) » vérifient la relation «  y = m x ». C'est-à-dire : «  » d’ où : ; Equation de la droite : .
Activité :
Déterminez , comme ci-dessus , l’équation de la droite passant par l’origine et le point « B ( - 7 ; 2 ) ».
Dessin d’une droite dont on connaît l’équation ( de la forme « y= mx » )							Info plus. ++++
Exemple 1 : Dans le plan muni d’un repère d’origine « O » (ci-contre). Nous allons dessiner la droite d’équation «  y = - 3 x ». Puisque la droite passe par l’origine, il suffit de connaître un autre de ses points. Par exemple : pour «  x = 1 » ; « y = -3 » Le point de coordonnés ( 1 ; -3) est un point de la droite. Placez –le . La droite cherchée passe par ce point et l’origine . Tracez - la.
Exemple 2 : Dessinons la droite d’équation : Pour « x = 1 » on a , le point déterminé par les coordonnées ( 1 ; ) n’est pas facile à placer avec précision. Il est préférable d’en choisir un autre dont les coordonnées sont des nombres entiers. Par exemple : «  x = 3 » on trouve « y = 4 » . A vous de terminer..
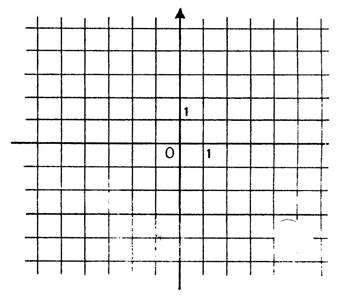
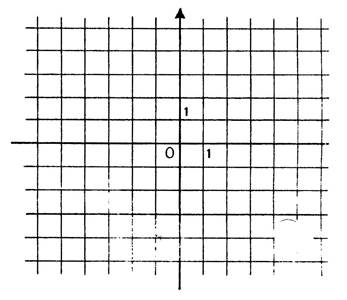
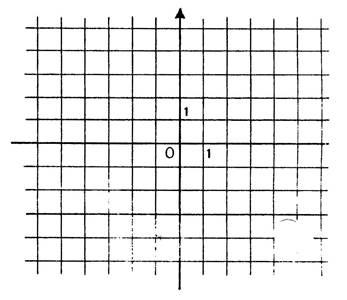
Activités : Dans le repère ci-contre , dessinez les droites (d ) ayant pour équations :

TRAVAUX AUTO FORMATIFS.

CONTROLE:

- Donner la procédure permettant de tracer une droite à partir d’un coefficient directeur et un point appartenant à la droite .

EVALUATION:

Tracer une droite : dont on connaît m = 3 ; et A ( -1 ; +2 )

corrigé CONTROLE:

Donner la procédure permettant de tracer une droite à partir d’un coefficient directeur et un point appartenant à la droite .

Procédure :

Equation de la forme « y = m x +p »

On connaît « m » et A ( x_A; y _A)

On place le point A

On place un point B dont les coordonnées sont

(x_A + 1) ; (y _A + m )

On trace la droite ( D) qui passe par les deux points

corrigé EVALUATION:

Tracer une droite : dont on connaît m = 3 ; et A ( -1 ; +2 )

Soit m = 3 ; et A ( -1 ; +2 )

Placer A ;

coordonnées x _A= -1 ; y _A=+2

On place un point B dont les coordonnées sont :

( x_A + 1) ; (y _A + m ) soit

(-1 + 1) ; (2 + 3 ) ;

soit les coordonnées de B ( 0 ; 5)