PRE REQUIS
Pour aborder sereinement : LES PROPORTIONS et les « GRANDEURS
PROPORTIONNELLES *» ;SCIENCES appliquées et
voir les supports théoriques relatifs aux domaines
traités(interdisciplinarités) il est nécessaire de revoir les rappels suivants:
*Ce sont les connaissances à maîtriser
pour aborder sereinement :LA FONCTION dite
« LINEAIRE » :
RAPPELS
|
FRACTION « EQUIVALENTE » *(à une autre
fraction): |
-* Cette notion est très importante ; elle
est la clef de voûte du travail sur la proportion et les proportionnalités.
- « Equivalente » :
veut dire « de même
valeur »; donc deux fractions
équivalentes sont des fractions qui ont la même valeur. ( on
dit aussi : même rationnel) .
(racine latine :« équi » qui signifie « égal »)
- Remarque .
Des fractions (ou écriture fractionnaire)peuvent représenter un même nombre:
exemple:
la division 48 / 12 = 4
20 / 5 = 4
4.8 / 1.2 = 4
4 / 1 = 4
on peut donc écrire que ![]() =
= ![]() =
= ![]() =
= ![]() = 4
= 4
A ) Deux
fractions séparées par le signe égale sont dites « fractions
équivalentes »
Modèle mathématique:
![]() =
=![]() (b et d sont
différents de 0)
(b et d sont
différents de 0)
B ) Des fractions équivalentes représentent un même nombre . ( même rationnel)
on peut donc écrire que ![]() =
= ![]() =
= ![]() =
= ![]() = (
4) sont des fractions
équivalentes)
= (
4) sont des fractions
équivalentes)
C ) Procédure
pour construction d’une fraction
équivalente (à une fraction donnée)
Pour construire une fraction
équivalente à une fraction donnée il suffit de multiplier le numérateur et le
dénominateur de la fraction par un nombre entier.
Modèle mathématique:
on
multiplie a et b par k ![]() =
= =
=![]()
IMPORTANT: MOYENS DE VERIFICATION
Pour
vérifier si deux fractions sont équivalentes ;Il y a deux solutions différentes :
Première
solution : on effectue les divisions et l’on compare !....
: On prend
une calculatrice ,on effectue les divisions relatives
à chaque fraction et l’on compare les deux résultats.(Il restera toujours un
doute notamment lorsque l’on divise des fractions irréductibles très proche ;
puisqu’elles n’ont pas de valeur décimale exacte).
(
Cette méthode peut être très utile pour classer des fractions ,les unes
par rapport aux autres)
exemple type I
Question: La fraction 11 / 15
est-elle équivalente à la fraction 13 / 17 ? (Si non ,on pourrait
alors demander de les classer par ordre ...croissant )
Réponse:
11 : 15 = 0.7333333
13 : 17 = 0.764705
conclusion: les fractions 11 /15
et 13 / 17 ne sont pas
équivalentes.
(Dans ce cas
,pour la question suivante , on peut écrire que 13 / 17
> 11 /15 )
exemple type II
Question :La fraction 22 /30
est-elle équivalente à la fraction
583/795 ?
Réponse:
22 : 30 = 0.733333333
583 :795 = 0.73333333
Conclusion :on ne peut conclure ,avec certitude ,on peut tout juste
déclarer : « elles pourraient
être équivalentes ».
Si on
ne peut conclure ,dans ce cas voir la solution
suivante
Deuxième
solution :on effectue « Le produit en croix » (méthode
la plus sûre)
Procédure permettant de vérifier si deux fractions sont équivalentes:
Pour
s’assurer (ou vérifier) que
deux fractions sont
équivalentes, il suffit de transformer l’égalité des deux fractions.
1°) On transforme
ce Modèle mathématique:
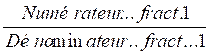 =
=
en une égalité de deux produits:
en ce modèle mathématique:
Numérateur..fract.1 x
Dénominateur. .fract 2
= Numérateur fract.2 x
Dénominateur fract
1
En résumé:
Deux fractions ( et
et 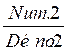 ) sont
équivalentes (c’est à dire) :
) sont
équivalentes (c’est à dire) :
 =
= 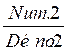 si Num.1 x
Déno.2 = Num.2 x Déno.1
si Num.1 x
Déno.2 = Num.2 x Déno.1
Lorsque nous aborderons la leçon
sur les proportionnalités on dira:
que le produit des extrêmes est égal au produit des moyens ,
(les extrêmes étants Num.1 et Déno.2, les moyens étants Déno.1 et Num.2)
Ce qu’il faut savoir :
CONTROLE:
Dans quel domaine des mathématiques utilise-t-on les fractions
équivalentes ?
Par quel signe sont séparées
deux fractions équivalentes?
Que représentent deux fractions
équivalentes?
Donnez le modèle mathématique représentant deux fractions équivalentes.
Donnez la procédure permettant d’obtenir un fraction
équivalent à une fraction donnée, donnez le modèle mathématique.
Comment peut-on procéder pour ordonner
( classer dans un ordre croissant ou
décroissant ) des fractions ?
Comment procède
-t - on pour vérifier si deux fractions sont équivalentes (donnez
la procédure la plus sûr?
Enoncer la procédure permettant d’effectuer « le produit en
croix ».
Ce
qu’il faut savoir faire :
EVALUATION:
I )Dire si les fractions suivantes sont équivalentes
(si non les classer par ordres croissant):
|
a) |
|
|
|
b) |
|
|
|
c)
|
|
|
II ) Construire .....5......fractions équivalentes à la fraction donnée
: ![]()
III)
On nous donne deux fractions ;![]() et
et ![]() ;sont-elles
équivalentes?
;sont-elles
équivalentes?
En
complément :voir cas avec nombres relatifs
I ° ) Construire 3
fractions équivalentes à la fraction donnée.(indiquer le coefficient
multiplicateur utilisé pour chaque étape)
*un
coefficient est un nombre entier
a) ![]()
b) ![]()
c) ![]()
d) ![]()
II ° ) Construire 4
fractions équivalentes à la fraction à la donnée
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) 
f)

G) ATTENTION :
IL faut ,pour trouver la réponse exacte aux
exercices suivants ; utiliser les « expressions
conjuguées » :
ces exercices
ne sont faisables que si vous avez travaillé les objectifs portant sur :
.
les
racines carrées (Objectif :Racine )
les
identités remarquables , (objectif
IDENTREM)
les
expressions ou quantités conjuguées (voir objectif : IDENTREM ,page 1/14)
Travail demandé : Trouver
une fraction équivalente n’ayant plus en dénominateur des radicaux
.
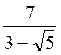 ;
; 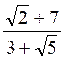
(on veut n ‘avoir au dénominateur que des nombres entiers ou
décimaux)
FIN DU
PREMIER RAPPEL.
SUITE du rappel :
I )
Voir
objectif DIVEUCLI. ;la division
euclidienne : « si le reste est égal à zéro ........ »
II )Voir l ’
objectif sur les fractions :
a) sur l’écriture d’une fraction
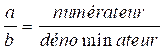
b) Construction de fractions équivalentes : 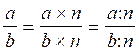
c) Addition
ou soustraction de fractions de même dénominateur
se souvenir que 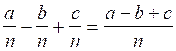
ATTENTION:
lorsque l'on additionne ou soustrait deux (ou plus) fractions de
même dénominateur , on n’a pas le droit
de modifier ce dénominateur ; donc dans l’exemple précédent on n’a pas le
droit de mettre comme dénominateur
« 3 n » ou « n3 »
REMARQUE IMPORTANTE :
LES PROPORTIONS METTENT EN JEU ,une
nouvelle opération mathématique,
NON PAS L ‘ADDITION ,LA SOUSTRACTION, LA DIVISION ou LA
MULTIPLICATION DE FRACTIONS , MAIS UNE CINQUIEME SITUATION MATHEMATIQUE
: L’EGALITE DE DEUX ( ou
plus) FRACTIONS.
TRAVAIL : Ce module comporte
trois objectifs
Les
GRANDEURS PROPORTIONNELLES :
Définition
de « grandeur » :
On
appellera « grandeur » tout
nombre associé à une unité.
Exemple : 3litres,2,5mètres
|
|
Nombre |
Unité |
|
un
mètre |
1 |
m |
|
3
litres |
3 |
l |
|
379
cm3 |
379 |
cm3 |
La division d’une grandeur sur une autre grandeur de même unité
s’appelle un « rapport »
LES TROIS OBJECTIFS A TRAVAILLER SONT :
|
Objectif n°
GP 1/3 rapports égaux |
|
|
Objectif n°
GP2/3 PROPORTION ET QUATRIEME PROPORTIONNELLE |
|
|
Objectif n°
GP3/3 Suites ;….. |