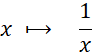Fiche 1 : Définition d’une application linéaire.

Fiche 2 : Représentation graphique d’une application linéaire.

Fiche 3 : Indications données par le coefficient directeur.

Fiche 4 : Propriétés des applications linéaires.

Fiche 5 : Situation problème.

Fiche 1 : Définition d’une application linéaire.

Chez  le super marché voisin,   l'essence coûte  1,50 €   le  litre.

Complète  le  tableau de  correspondance  entre  le nombre de  litres  (L)  et  le prix ( € ).

Essence en L

1

2

3

5

0,6

1,5

20

50

→

Prix   ( en  € )

1,5

3

4,5

7,5

0,9

2,25

2/3

30

57,5

←

On passe de la première ligne à la deuxième en multipliant chaque nombre par       ………..

On est donc en présence d'une relation de proportionnalité.

On dit que le prix à payer est fonction du nombre de litres.

(lire « à pour image »)

Nombre de litres « L »

Prix   ( en  € )

5

On dit que : « 7,5 » est l’image de « 5 »

20

On dit que : « 30 » est l’image de « 20 »

En désignant par  un nombre quelconque et par  le nombre qui lui correspond, on peut écrire :

       x          ;           est  fonction   de

 Le procédé qui, au nombre de litres, fait correspondre le prix s'appelle une fonction.

Dans le cas où le procédé consiste à multiplier par un nombre déterminé,  on dit que cette fonction est une fonction linéaire ou une application linéaire.

Le coefficient multiplicatif « 1,5 »   qui est le coefficient de proportionnalité est alors appelé le coefficient de l'application linéaire (ou coefficient de linéarité).

D'une manière générale,

Toutes les fois qu'il y a proportionnalité, on peut parler d'application linéaire.

En désignant par "" le coefficient de proportionnalité,  l'application linéaire correspondante est le procédé qui a tout nombre fait correspondre ce nombre multiplié par «  »,

(inversement toute application linéaire définit une situation de proportionnalité).

A retenir

Pour tout nombre « » , dire que «  » est l’image de « x » par l’application linéaire de coefficient «  » , c’est dire que  «  x » .

On l’écrit :    

Exemple 1 :  Une automobile roule à la vitesse constante « v » de 90 km/h .

La distance "" qu'elle parcourt est proportionnelle au temps "  ".

Application linéaire correspondante :           et on peut écrire

Exemple 2

La longueur  "C" d'un cercle est proportionnelle à son rayon "".

Application linéaire correspondante :  R        et on peut écrire

Autre question :

L'aire "" du disque correspondant est  ;  La relation est-elle linéaire ?  ( non, c’est une fonction du second degré)

Activité exercices:

«  »   désignant un nombre quelconque, dans chacun des cas ci-dessous,  dites (par oui ou non) s'il s'agit d'une            application linéaire.

Oui :  

Oui : Oui :  

Non

Voir :Fonction inverse dite « homographique »…

Oui :  

Fiche 2 : Représentation graphique d’une application linéaire.

Info ++@ ++++

Nous considérons l’application linéaire de coefficient :    .

«  » désignant un nombre quelconque et « » son image, on peut écrire 
      ;  

Ayant choisi deux axes de coordonnées, la représentation graphique de cette application linéaire est constitué par tous les points dont l’abscisse est un nombre « » quelconque et dont l’ordonnée est «  » est   :     de «  ».

Choisissons quelques points .

Activité : Complétez le tableau ci-dessous :

-4

-2

-1

0

1

2

4

-6

-3

-1,5

0

1,5

3

6

Placez ces points . Vous constatez qu’ils sont alignés ..

Tracez la droite passant par ces points. Vous remarquez qu’elle passe par l’origine des axes de coordonnées.

·       Ce que vous venez  de constater, on peut le démontrer, nous ne le ferons pas ici, et vous  admettrez qu'il en est ainsi pour toutes les applications linéaires.

Remarque :

La droite que tu as tracée passe par le point de coordonnée (1 ;1,5)

L'ordonnée de ce point n'est autre que le coefficient  de l'application linéaire

On l'appelle le coefficient directeur de la droite.

A retenir

La représentation graphique, d'une application linéaire, de coefficient  "  " est une droite, passant par l’origine, des axes  de coordonnées et par le point de coordonnée. ( ). 

« a »   est  appelé le  coefficient directeur de la droite.

Remarque

Dans le cas où les axes de coordonnées sont perpendiculaires et où les unités sont les mêmes sur les deux axes, le coefficient directeur est appelé pente de la droite.

Activité : Vous allez faire la représentation graphique de l’application linéaire vue dans la fiche 1.

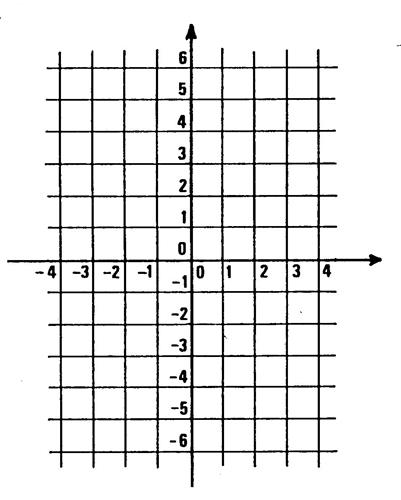
Les nombres considérés étant positifs on se placera dans le quart de plan délimité par les deux demi-axes de coordonnées ci-contre.

La représentation graphique est alors une demi-droite. On sait qu'elle passe par l'origine des axes de coordonnées. Pour pouvoir la tracer, il suffit de connaître un autre point On le choisit alors dans le tableau de la fiche 1.

Pour avoir une meilleure précision, il est préférable de prendre ce point le plus loin possible de l'origine. vous choisissez  alors le point de coordonnées  (_  ,   ). Placez ce point et tracez la demi-droite.

Essence en L

5

11

Prix en  €

27

31,5

Fiche 3 : Indications données par le coefficient directeur.

Dessinez ci-contre les droites représentant les applications linéaires définies ci-dessous.

« d₁ » ; 

« d₆ » ; 

« d₂ » ; 

« d₇ » ; 

« d₃ » ; 

« d₈ » ; 

« d₄ » ; 

« d₉ » ; 

« d₅ » ; 

« d₁₀ » ; 

Vous pouvez faire (verbalement ) certaines constatations.

Fiche 4 : Propriétés des applications linéaires.

Reprenons  l'application linéaire de la fiche 1 ; 

1^ère propriété : Considérons une partie du tableau.

« 2 » a pour image « 3 » ; « 3 » a pour image « 4,5 ».

« »

2

3

5

« »

« 2 + 3 =    5 » ; « 5 » a pour image « 7,5 »   ;  Or « 3 + 4,5 »  =  7,5 

Vous pouvez constater qu’il en est ainsi avec n’importe quels nombres.

D'une manière générale, étant donné une application linéaire de coefficient « »,    «  » et « »  étant des nombres quelconques, l'image de « » est «  » , l'image de «  » est      «   » ;

 L'image de  est… …………... En développant on obtient  

On peut donc dire

2^ème  propriété Reprenons une partie du tableau de la fiche 1.

« 2 » a pour image . « 3 » ;  « 20 »  a pour image «  30 »

2

20

3

30

Or :        et 

Vous  pouvez  constater qu'il en est ainsi avec n'importe quels nombres.

D'une manière générale, étant  donné une application linéaire de coefficient ,

 étant un nombre quelconque, l'image de  est .

 étant un nombre quelconque, l'image de  est  .

Or grâce à  l’ associativité et la commutativité, on peut écrire

On peut donc dire : 

A retenir :

Pour toute application linéaire ,

-        L’image de la somme de deux nombres est égale à la somme des images de ces nombres,

-        L’image du produit d’un nombre par un nombre « k » est égale au produit de « k » par l’image du nombre.

Activité exercice :

Une pompe débite 15 L d'eau en 6s. Sachant que le débit est constant,  c'est-à-dire que l'écoulement est une fonction linéaire du temps, complétez le tableau donnant la quantité d'eau écoulée en fonction du temps.

( Débit par s  = 15 / 6 = 2,5 L /s )

Temps ( en s)

3

2

6

10

12

7

8

14

Quantité d’eau ( en L)

7,5

5

15

25

30

20

35

Quelle est le débit de cette pompe ? …2,5. L/s     ; …(2,5 fois 60 =  150)…….L/min ;  …( 150 fois 60 = 9 000  L / h) soit  …9. m³/h

(info ++sur les conversions ++)

Fiche 5 : Situation problème.

Paul   vient de participer à un  raid : « les 50km de la foret de Saint-Gobain ».«  50km »  est la longueur du  tracé en circuit fermé.

La route étant plate, on considérera que tous les concurrents courent (ou marchent) à vitesse constante, c'est-à-dire que le chemin parcouru est une fonction linéaire du temps.

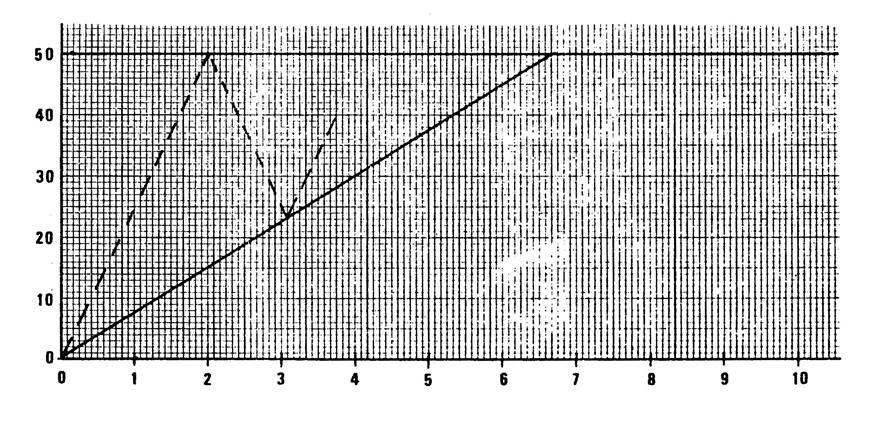
Rentré chez lui, Paul  fait le graphique ci-dessous :

En abscisse, il porte le temps (en heure), l'heure de départ étant l'heure 0.  ( t ₀)

1 h est représentée par  …….mm donc 1mm correspond à  …….min.

En ordonnée, il porte les distances en km (1 km est représenté par      mm).

Il marque  « départ » le point « km 0 » et le  point « arrivée »,  au « km 50 ».

1°) La portion de droite (en trait plein) tracée sur le dessin est la représentation graphique du chemin parcouru par Paul en fonction du temps.

Lisez sur ce graphique l'heure d'arrivée de Paul  au point  « km 50 » : …………………..

Vous allez  déterminer sa vitesse de plusieurs façons :

-        Lisez   sur le graphique la distance parcourue en 1 h : _____ .   La vitesse est donc ___ km/h .

-        Lisez   sur le graphique la distance parcourue en 5 h : ____ ___

Sachant que   sa vitesse est donc :  

Paul a parcouru les 50km en 6 h 40 min ;  or   6 h 40 min =   400  min ; soit le rapport :  

Donc       ;   v  =  ( 50 km )  ( 6 h 40 min)   =  (50 km ) =  (50 km )= ..7,5 km / h…

2°) Victor  est passé au 20^ème  km au bout de 3 h 20 min .

Tracez  la représentation graphique. Lisez  l'heure d'arrivée : ……………………………………                  

Calculez   sa vitesse. Vous  trouvez :  …………………………………………………….. ;         

Vérifiez par le calcul son heure d'arrivée. Vous trouvez.

3°) A mi-chemin (au bout de 25km) , Paul  apprend que son ami Pierre est passé par là il y a 40min . Tracez la représentation graphique du déplacement de Pierre,

Quelle sera l'avance de Pierre sur Paul à l'arrivée ?       

Calcule la vitesse de Pierre . Vous  trouvez : …………………………..

4°) David a fait le trajet à la vitesse de 12,5km/h. Tracez la représentation graphique.

Lisez sur le graphique son heure d'arrivée :…………………. Vérifiez par le calcul ;   

A ce moment-là, combien de km reste-t-il à parcourir pour Paul  ?
Lecture sur le graphique :…………….. ; Par le calcul, vous  trouvez :………………………………..

5°) Le premier a fait le parcours en 3 h 05 min . Quelle est sa vitesse ?          

Tracez sa représentation graphique et lisez la distance parcourue en 1 h 40 min :   

Vérifiez par le calcul. Vous trouvez :………………………………………..

6°) Lucile  est une adepte du vélo. Elle prend le départ avec les concurrents. Mais arrivée à « km 50 », elle repart en sens inverse jusqu'à ce qu'elle rencontre Paul. Elle fait alors demi-tour pour aller à « km 50 »,  puis elle revient à la rencontre de Paul   et ainsi de suite jusqu'à l'arrivée de  Paul.
La représentation graphique du déplacement de Lucile  a été amorcée ( en traits pointillés). A vous  de la terminer (la vitesse de Lucile  à vélo est 25 km/h
Quelle est en km, la distance parcourue par Lucile ?

Fait le 6/1/2015