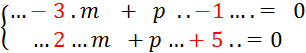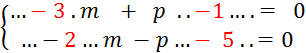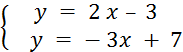CORRIGE	Classe de 3^ème collège
Les équations de droites ( tracés )		Programme de 3^ème collège.
Pré requis:
Droites et repérage
Droites dans un repère cartésien…
Les repères cartésiens

ENVIRONNEMENT du dossier:

Index

AVANT : 1°) Coefficient de droite. 2°) Voir les fiches 3^ème collège. 3°) Droites dans un repère .

COURS

APRES : 1°) Les droites croissante ; décroissante,.. 2°)le parallélisme et la perpendicularité 3°) Fonction affine : représentation graphique 4°) Calculs. 5°) Fonction affine : équations.

Complément d’Info : Liste des objectifs cours sur la fonction affine et ses pré requis . liste des cours dans le repérage. Liste des cours d’algèbre

TITRE : ETUDE D’ UNE DROITE DANS UN REPERE:

Les équations de droites ( tracés ) Classe de 3^ème collège

Fiche 1 : Diverses positions d’une droite suivant son équation.

Fiche 2 : Détermination de l’équation d’une droite.

Fiche 3 : Comment lire sur le dessin une équation de droite :

Fiche 4 : Intersection de deux droites.

Fiche 5 : Droites perpendiculaires ( dans un repère orthonormal )

Fiche 6 : Situation problème.

Travaux ; devoirs			Corrigé
TEST	Contrôle	évaluation	Contrôle	évaluation

Interdisciplinarités : (matière concernée)
F	H	Géo.	Vie quotidienne et vie familiale	Autres :	Sciences et technique	Physique Chimie Electricité	Statistique.

Pour en savoir plus : Pour chaque chapitre il y a un retour au cours , il faut cliquer sur « info + »

<<< Retour vers les fiches.

Fiche. Les équations de droites ( tracés )

Fiche 1 : Diverses positions d’une droite suivant son équation.

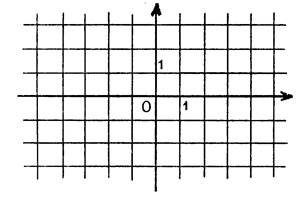
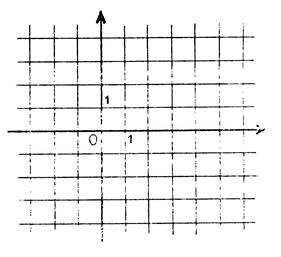
Une droite est parfaitement déterminée quand on connaît son équation : «   ». Les valeurs de «  » et de «  » déterminent sa position par rapport au repère : · « m » , le coefficient directeur , donne l’inclinaison de la droite par rapport aux axes. · « p » est l’ordonnée du point d’intersection de la droite avec l’axe des ordonnées. Dans chacun des cas ci-dessous, dessinez ( en rouge)la droite dont on donne l’équation. ( Le repère est orthonormal ).

«   » et «   »

«   »

«   » et «   »

«  »

«   » et «   »

«   »

«   » et «   »

«   »

«   » et «   »

«  »

«   » et «   »

«   »

«   »

«  »

Cas particuliers

«  »

«   »

Cas particuliers

«   »

Droites dont l’équation n’est pas de la forme «  y« = mx + p »

«  »

Cas particuliers

«   »

Fiche 2 : Détermination de l’équation d’une droite.

Info +++++

Exemple 1 : Tracer la droite « d » passant par « A ( 4 ; 3 )» et de coefficient «  » . Nous allons déterminer l’équation de « d ». Cette équation est de la forme «  y = m x+ p » « A est un point de « d » » Puisque «  » , l’équation s’écrit «   »

« A est un point de « d » » se traduit par : « les coordonnées de « A » vérifient l’ équation de « d ». C'est-à-dire : «   » et après simplification , «  » d’ où «   » La droite « d » a alors pour équation : «  »

Exercice 1 : «  » ( lire « delta ») est une droite ayant pour équation : «  » Déterminez l’équation de la droite «  » passant par le point «  B ( - 1 ; 2) et parallèle à «  » . Dessinez les droites «  » et «  » .

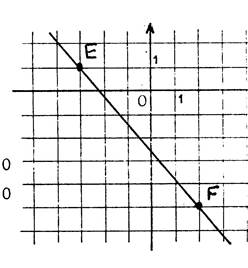
Exemple 2 : Placez les points «   » et «  ». Tracez la droite «  » passant par «  » et « ». Déterminons l’équation de «  » ( de la forme «   ») «E » est un point de « D » » se traduit par : « les coordonnées de « E » vérifient l’ équation de « D ». ( il en est de même pour « F »). On écrira alors :

Pour « E » :  »

C'est-à-dire

Pour « F » :  »

Vous êtes en présence d’un système d’équations de couple inconnu ( m ; p ). A vous de le résoudre……..

( on a multiplié par « -1 » le deuxième ligne ) ; ; on additionne :  ; On reprend une des équation de départ pour trouver la valeur de « p » : :  » ; :  » :  ; «  » Le droite « D » a alors pour équation « y = …………… » D’où l’équation de la forme  «   » passant par les deux points est «  »

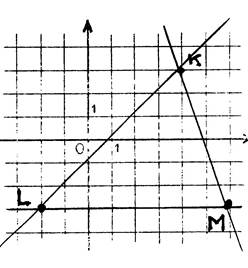
Exemple 3 : Dans le plan muni d’un repère orthonormal, on donne les points : Placez ces points et tracez le triangle « KLM ». Déterminez l’équation de chacune des droites supports des côtés du triangle « KLM »

Fiche 3 : Comment lire sur le dessin une équation de droite :

Voir : tangente ….

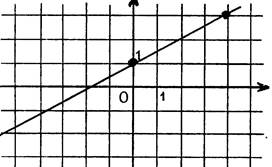
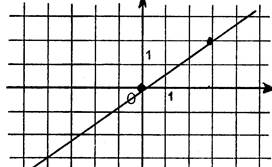
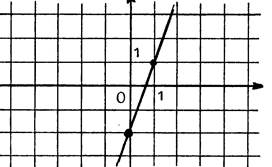
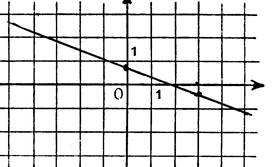
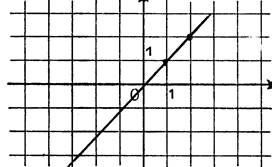
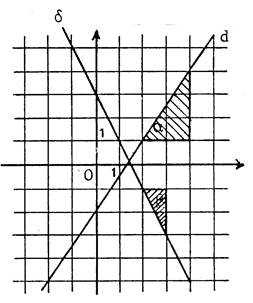
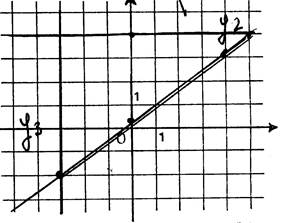
Par lecture sur le dessin , nous allons déterminer les équations de droites « d » et «  ». Ces équations sont de la forme «   ».

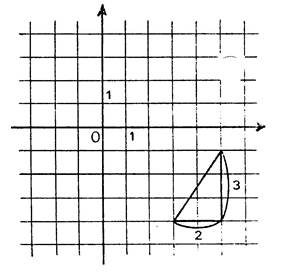
· Droite «  » : «  » étant l’angle de «  » avec l’axe des abscisses, « m » étant positif , vous savez que . En considérant le triangle rectangle hachuré , vous pouvez écrire : . D’autre part, vous savez que le point d’intersection de la droite avec l’axe des ordonnées a pour coordonnées Vous lisez alors sur le dessin : …………… La droite «  » a pour équation «  »

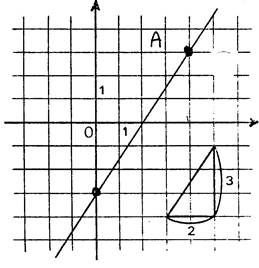
· Droite «  » : «  » étant l’angle de «  » avec l’axe des abscisses . « m » est négatif , vous savez que . En considérant le triangle rectangle hachuré , vous trouvez : d’où «   » Vous lisez comme précédemment : «   » La droite «  »  a pour équation «  »

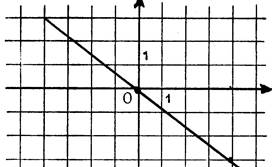
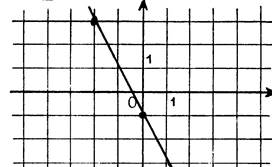
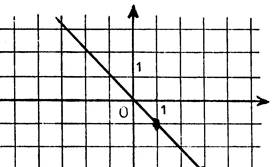
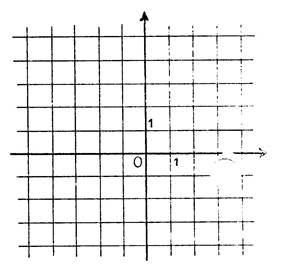
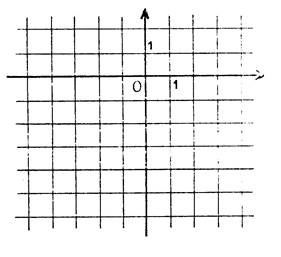
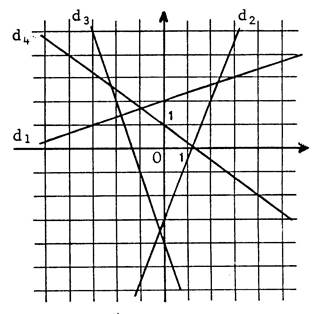
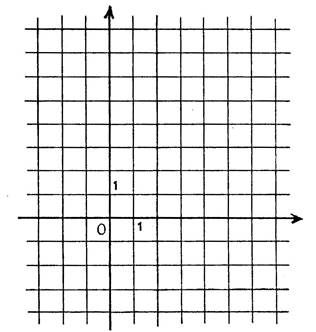
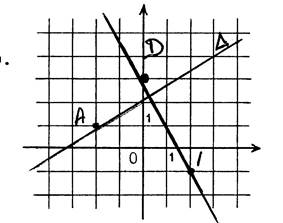
Exercice : Lisez sur le dessin ci-contre l’équation de chacune des droites : ……………………………………………………….. ……………………………………………………… ……………………………………………………… ………………………………………………………

Fiche 4 : Intersection de deux droites.

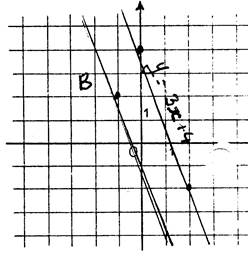
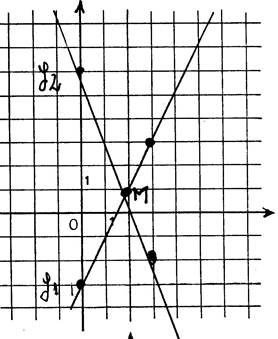
Exemple 1 : Deux droites ont pour équations respectives : «  » et «  ». Activité : · Dessinez ces droites. · Elles n’ont pas la même direction car elle n’ont pas le même coefficient directeur .donc elles se coupent. Soit « M » le point d’intersection. Lisez sur le dessin les coordonnées de « M ». M ( …. ; ….)

· « M » étant un point commun aux deux droites, ses coordonnées vérifient chacune des équations. Donc les coordonnées de « M » sont solutions du système :

A vous de résoudre ce système………………………..

Activité : Les droites ;  ; ; ont pour équations respectives : «  » ; «  » ; «  » Calculez les coordonnées des points d’intersection de ces droites. Dessinez ces droites et contrôlez sur le dessin.

Fiche 5 : Droites perpendiculaires ( dans un repère orthonormal )

Info +++ sur …..

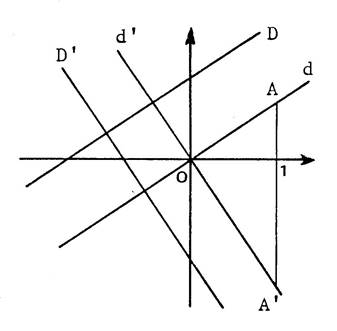
Le plan est muni d’un repère orthogonal d’origine « O ». « D » et « D’ » sont deux droites d’équation respectives «   » et «  ». « d » et « d’ » sont respectivement parallèles à « D » et à « D’ » passent par « O ». « d » et « d’ » ont alors pour équations respectives : «   » et «  »

Appelons « A » le point de « d » d’abscisse « 1 » «  A ( …. ;…..) » Appelons « A’ » le point de « d » d’abscisse « 1 » «  A’ ( …. ;…..) » · Calculons OA² ; OA’² et AA’² ……….). donc «   » . ; donc «   » c'est-à-dire Donc

· Si « D » et « D’ » sont perpendiculaires , « d » et « d’ » le sont aussi . Donc le triangle «  » est rectangle . Grâce au théorème de Pythagore , on peut écrire : C'est-à-dire ( en reprenant ce que nous avons trouvé ci-dessus) :

et après simplification : c'est-à-dire :

«   »

Inversement : Si «  » , en faisant les calculs en sens inverse , on démontre grâce à la réciproque du théorème de Pythagore que le triangle « AOA’ » est rectangle en « O » c'est-à-dire que « d » et « d’ » sont perpendiculaires ainsi que « D » et « D’ ».

Théorème : Etant donné , dans le plan muni d’un repère orthogonal , deux droites «  » et «  » d’équations respectives «   » et «  », si «  » et «  » sont perpendiculaires alors «   » Si «  » alors «  » et «  » sont perpendiculaires.

Activité 1 : Dans le plan muni d’un repère orthonormal tracez la droite « D » d’équation «  y = -2x +3 » et la droite passant par « A ( - 2 ; 1 ) et perpendiculaire à « D ». Déterminez par le calcul l’équation .

Activité 2 : Déterminez l’équation de chacune des hauteurs du triangle « KLM » de l’exercice « 2 » de la fiche 2. Calculez les coordonnées de l’orthocentre du triangle « KJM » . Rédigez vos calculs sur une autre fiche.

Fiche 6 : Situation problème.

Le plan est muni d’un repère orthonormal. Vous compléterez la figure tout au long du problème. « d » est la droite d’équation : «  »

1°) «  » est le point de «  » d’abscisse «  » , calculez son ordonnée. ; « » est le point de « d » d’ordonnée «  » , calculez son abscisse. 2°) Tracez la droite «  » et placez «  » 3°) Déterminez l’équation de la droite ( ). 4°) La parallèle à (BC) passant par « A » et la parallèle à ( AB ) passant par « C » se coupe en « D ». Déterminez les équations de ( AD ) et de ( BC) . 5°) Calculez les coordonnées de « D ». 6°) Déterminez les équations des droites ( AC ) et de ( BD) . 7°) ( AC ) et ( BD) se coupent en « I ». Calculez les coordonnées de « I ». 8°) Vérifiez par le calcul que « I » est le milieu de et de . 9°) Démontrez que ( AC) et (BD ) sont perpendiculaires. Quelles la nature de « ABCD » ? ( Démontrez – le )

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) Par définition quelle est la forme de l’équation d’une droite (D) ?

1°) Compléter les phrases :

a) Tous les points du plan dont les coordonnées ( x , y ) vérifient l’égalité : y = m x + p , sont …………………………………………..

b) Si un point est sur (D) alors ……………………………………………………

c) x = k est l ‘équation d’une : ………………………………………………..

d) y = p est l’ équation d’une …………………………………………………..

2°) dans l’équation de la forme «  y = ax +b » quel nom donne - t-on à « a » et à « b »

3°) Donner la procédure permettant d’établir l’équation d’une droite dont on connaît : On connaît un point de la droite A ( x₁ ; y₁)  et son coefficient directeur « m ».

4°)Donner la procédure permettant d’établir l’équation d’une droite dont on connaît deux points appartenant à la droite.

5°) Soit l’équation de la forme « y = m x + p » si « m = 0 » que faut - il conclure ?

6°) Soit l’équation de la forme « y = m x + p » si « y = 0 » que faut - il conclure ?

(on posera «  - p/m  = P »

7°) En règle générale, que faut -il connaître , au plus simple , pour tracer une droite dans un repère ?

8°) Qu’indique le coefficient directeur d’une droite ?

9°) Compléter la phrase :

La valeur absolue du coefficient directeur est égale ………………………………………………………………………………………….

10°) Quel est la nature du nombre représentant le coefficient directeur d ‘ une droite ?

11°) Quelle est la formule qui permet de calculer le coefficient directeur d’une droite :

12°) si m > 0 , que peut - on conclure ?

13°) si m < 0 , que peut -on conclure ?

14°) On nous donne deux équations de droite. Quand peut on dire que ces deux droites sont « parallèles » ?:

15°) On nous donne deux équations de droite. Quand peut on dire que ces deux droites sont « perpendiculaires ou orthogonales » et non parallèles aux axes ? 

EVALUATION:

1. Dans un repère orthonormal, on considère les courbes suivantes :

(C₁ ) : y = -2x +1 ; (C₂ ) : y = x² + 3 y² = 5 ; (C₃ ) : y = 7x ; (C₄ ) : y = x y + 3 x = 0 ; (C₅ ) : y = 5 ; (C₇) : y = 3x + 6 y - 10 = 0

Parmi ces courbes, quelles sont celles qui sont les représentantes d’une droite ?

2 . Dans un repère orthonormal , soit la droite (D) : y = 6 1,5 x + 2,5

Dire si les points suivants appartiennent à la droite (D) :

A ( 2 ; - 5) ; B ( 0,2,5 ) ; C ( -1 ; -1 ) et F (-6 ; 5 )

3 . Dans un repère orthonormal, on considère les droites :

D₁ : y = 2x + 5 ; D₂ : y = - 3 x + 8 ; D₃ : y = x - 7 ; D₄ : y = - x + 1

Déterminer le coefficient directeur de chacune de ces droites

4. Dans un repère orthonormal , soit la droite ( D) : y = -0,5 x + 2

a) déterminer les ordonnées des points A ; B ; C et D d’abscisses respectives : 1 ; 4 ; -7 et -2

b) Déterminer les abscisses des points E ; F ;G et H d’ordonnées respectives : 1 ; 4 ; -7 et -2

5 . Dans un repère orthonormal , tracer les droites :

(D ₁ ) de coefficient directeur « -1 » et passant par le point de coordonnées ( 0 ; 2 ) ;

(D ₂ ) de coefficient directeur « 0,5 » et passant par le point de coordonnées ( 0 ; -1 ) 

(D ₃ ) de coefficient directeur « -1,5  » et passant par le point de coordonnées ( 1 ; -3 ) 

(D ₄ ) de coefficient directeur « 2 » et passant par le point de coordonnées ( -1 ; 1 ) 

6. . Dans un repère orthonormal, tracer les droites :

D₁ : y = 2x + 5 ; D₂ : y = - 3 x + 8 ; D₃ : y = x - 7 ; D₄ : y = - x + 1

7. Dans un repère orthonormal , déterminer une équation de la droite ( D) passant par le point A ( 0 ; 5 ) et B ( -2 ; 3 )

8 . Dans un repère orthonormal , déterminer une équation de la droite ( D) passant par le point A ( - 1 ; 4 ) et dont le coefficient directeur est «  m = -4 ».

9. Déterminer une équation de chacune des droites ( D ₁ ) ; ( D ₂ ) et ( D ₃ ) données dans le repère orthonormal ci contre.

10. Dans un repère orthonormal , soit la droite ( D) dont une équation est y = 3x + 5 . Parmi les droites suivantes :

D₁ : y = 3x + 2 ; D₂ : y = 3 x + 0,5  ; D₃ : y =-3 x + 0,5  ; D₄ : y = 0,5 x + 4

Quelles sont celles qui sont celles qui sont parallèles à la droite ( D) ?

11. Dans un repère orthonormal, soit la droite ( D) dont une équation est « y = 3x +5 »

parmi les droites suivantes :

D ₁ : ; D₂ =  ; D ₃ =  ; D ₄ = y = 3 x + 4

Quelles sont celles qui sont perpendiculaires à la droite ( D) . ?