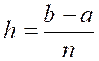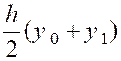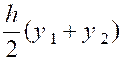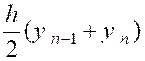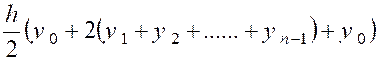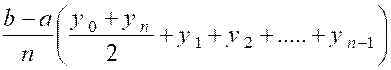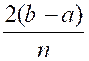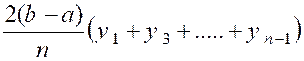Pré requis:
|
Info : liste des connaissances en algèbre
préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°)
L’intégration par parties. |
APRES :
|
Complément
d’Info :
1°)
Liste
des cours : prépa concours
A consulter pour compléments : |
|
|
|
|
|
|
|
TITRE : niveau
III : LES INTEGRALES : METHODE DES TRAPEZES.
|
|
|
|
|
|
|
|
|||
|
Voir
l’évaluation !!! |
|
Contrôle |
évaluation |
||
|
|
|
||
|
|
|
|
|
|
|
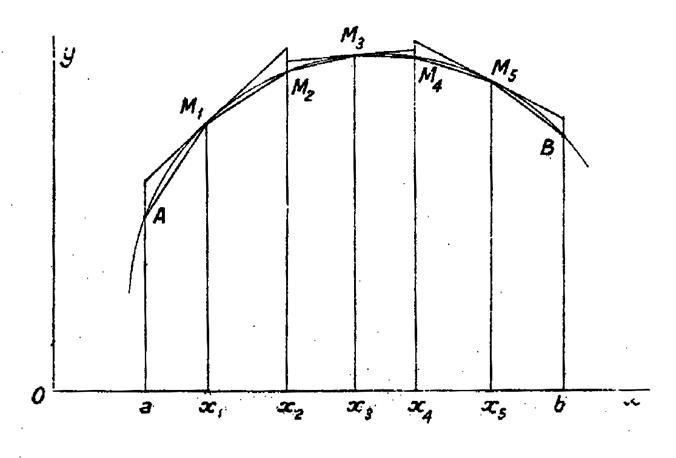
Partageons l’intervalle ( a ;
b) en parties égales. Soient « x1 ; x2 ;……x n-1 » ;
les abscisses des points « M 1 ;
M 2 ; M3 ;……. ;M n-1 » ,
ainsi obtenus sur la courbe ; et soient « |
|
|
|
|
La somme des aires des trapèzes inscrits
constitue une valeur approchée de l’aire de la courbe. Tous ces trapèzes ont pour hauteur : L’aire du premier trapèze est « Celle du second est « Celle du dernier « |
|
|
|
|
D’où la valeur approchée de l’intégrale. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Remarque : Supposons de plus que dans l’intervalle ( a ;b) la concavité ne change pas de sens. On peut
toujours se ramener à ce cas en supposant qu’on ait d’abord divisé
l’intervalle donné en intervalles partiels tels que dans chacun d’eux la
courbe ne présente pas de points
d’inflexion. |
|
|
|
|
Dans ce cas , on peut
trouver une limite supérieure de l’erreur commise en partageant l’intervalle
( a ; b) en un nombre pair de parties égales. |
|
|
|
|
|
|
|
|
|
En effet, menons les tangentes à la courbe aux points
d’abscisses « x1 ;
x2 ;……x n-1 » |
|
|
|
|
|
|
|
|
|
Nous obtenons ainsi des trapèzes circonscrits et
l’aire de la courbe est comprise entre la somme des aires des trapèzes inscrits,calculée précédemment
, et la somme des aires des trapèzes circonscrits. |
|
|
|
|
|
|
|
|
|
Sur la figure ci-dessus ,
où la concavité est dirigée du côté « y » négatifs, les trapèzes
inscrits donnent une valeur approchée par défaut , et les trapèzes
circonscrits une valeur approchée par
excès. Ce serait le contraire si la concavité était dirigée du côté
des « y » positifs. |
|
|
|
|
|
|
|
|
|
Ceci posé , l’aire du
premier trapèze est égale au produit de la hauteur
La différence entre la somme des aires des
trapèzes inscrits et circonscrits constitue une limite supérieure de l’erreur
commise. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||