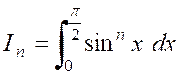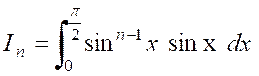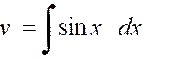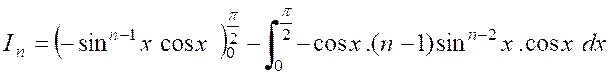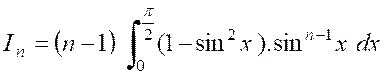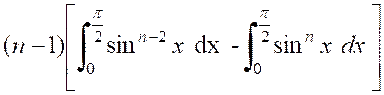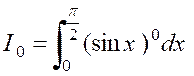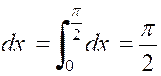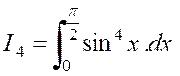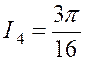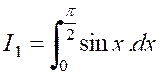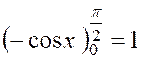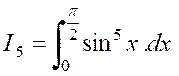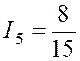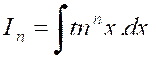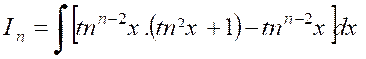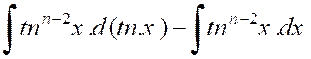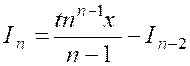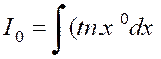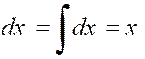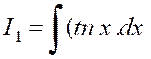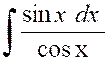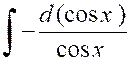COURS

Soit une intégrale «  »    contenant un indice « n » ,on peut souvent établir une formule de récurrence , ou de réduction,permettant de ramener le calcul de «  »   à celui d’une intégrale d’indice moins élevé.

C’est , par exemple , le cas de l’intégrale :  ,                « n » étant un exposant entier et positif.

Intégrons par parties , en nous arrangeant pour retrouver une intégrale de même forme ;

A cet effet , écrivons «  »  sous la forme :

Et posons :                et    

On en déduit :

Et    ;

Par suite :

La partie intégrée est nulle pour « x = 0 »et pour « x= » .

Il reste :

 =    de la forme

D’où la formule  «  »

Deux cas sont  à distinguer :

1°) Si « n » est pair , on ramène le calcul de «  » à celui de  =

Exemple :

Soit     , On a    ; puis  

D’où , en multipliant membre à membre :    d’ où  

2°) Si « n » est impair, on est ramené à  «  »

  = 

Exemple :    ,   on a :     ;   ,  d’où                    et 

Remarque : presque toutes les  formules de réduction s’obtiennent en intégrant par parties. Quelques –unes cependant, se trouvent autrement.

Exemple :

Soit :    , « n » étant entier et positif.

Nous savons ( info ++) que « d ( tn x) = ( 1 + tn ² x ) dx »

Ceci nous conduit à écrire :

 = 

d’où :

cette formule ramène le calcul de «  » à celui de «  » si « n » est pair ou «  » si « n » est impair.

On a d’autre part :

  = 

Et

   =  =  =

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Voir le cours !!!!!