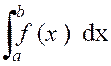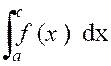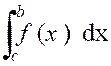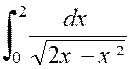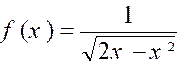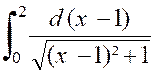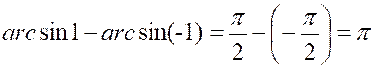Pré requis:
|
Info : liste
des connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°) L’intégration par parties. |
APRES :
|
Complément d’Info :
1°) Liste des cours : prépa concours
A consulter pour compléments : |
|
|
|
|
|
|
|
TITRE :niveau
III : LES INTEGRALES : CAS OU LA FONCTION DEVIENT INFINIE.
|
|
|
|
|
|
|
|
|||
|
Voir
l’évaluation !!! |
|
Contrôle |
évaluation |
||
|
|
|
|
|
|
|
|
|
|
Soit l’intégrale : Supposons de plus que la fonction « |
|
|
|
Comme d’autre part ( voir cours sur :l’intégrale définie) « On peut toujours se ramener au cas où la fonction
devient infini pour l’une des limites d’intégration, Ceci étant , soit
«
la fonction « |
|
|
|
Il peut se faire que «
On calcule de même l’intégrale « Exemple : L’intégrale peut s’écrire : ( voir
cours sur :l’intégrale définie)
|
|
|
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||