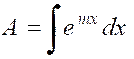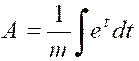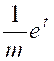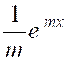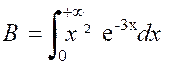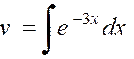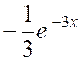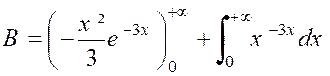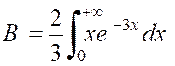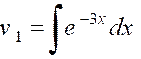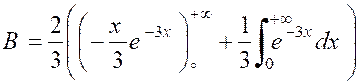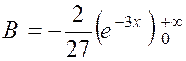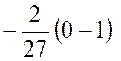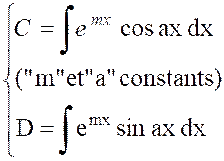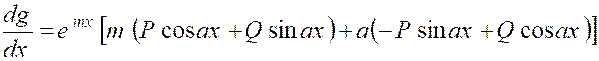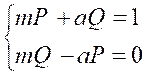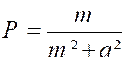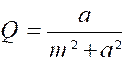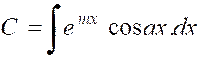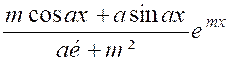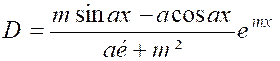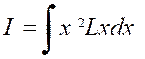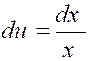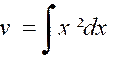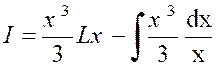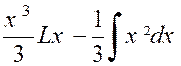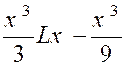COURS

Soit l’intégrale    (voir tableau :intégrales usuelles)

Posons « m x = t » , d’ où  «  m dx = dt »

On a alors :

  =              =       

Supposons maintenant que l’intégrale contienne à la fois une exponentielle et une puissance de « x » .

On fait alors disparaître cette puissance en intégrant par parties.

Exemple :

Posons « x² = u »  et   «  »   , on en déduit

«  du = 2 x  dx »

«  =

Et

La partie intégrée est nulle .En effet   pour « x = 0 » , elle est la forme «  0 x 1) ; et pour «  » on a l’indétermination «  », mais c’est l’exponentielle qui l’emporte sur le nombre et qui donne sa valeur au produit , soit  « zéro ».

Il reste donc :

Intégrons à nouveau par parties en posant : « x = u »   ;  «  »

D’où    «   » ; « =

D’où « 

*   =    =

Calcul des deux intégrales :

Pour donner un exemple d’une méthode assez générale , l’identification,essayons de prévoir la forme du résultat.

L’intégrale « C », par exemple, est une fonction ayant pour dérivée « e^mx cos a x »

Il est certain que la fonction suivante «  g (x) = e^mx ( P  cos ax  + Q sin ax) »  dans laquelle « P » et « Q » sont des constantes a une dérivée de la forme :

         «  g (x) = e^mx ( P₁  cos ax  + Q₁ sin ax) »

« P₁  et  Q₁ » étant d’autres constantes. IL n’est donc pas impossible que l’on puisse déterminer « P  et  Q » de manière que « P₁ = 1  et  Q₁ = 0»

Détaillons le calcul , on a :

 ; 

On doit donc avoir :    d’où l ’ on tire      et    et part suite

  = 

on trouve de même :

Soit enfin une intégrale contenant à la fois « Lx » et une puissance « x ».On fait disparaître le logarithme en intégrant par parties.

Exemple. Soit l’intégrale :

Posons «  L x = u »   et «  x² dx = dv »

On en déduit :    et     =

D’où :

  =  = 

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Voir le cours !!!!!