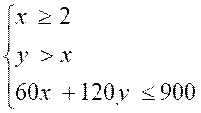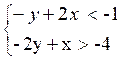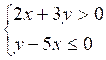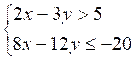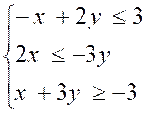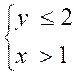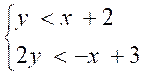|
Résolution de
l’équation du premier degré à deux
inconnues |
|
|
Fonction linéaire
(représentation graphique) |
|
|
Fonction affine
(représentation graphique) |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : |
Objectif
suivant : |
DOSSIER
: Résolution de SYSTEMES de 3 INEQUATIONS
du PREMIER DEGRE à deux INCONNUES
· Résolution graphique d’un SYSTEME
à 3 INEQUATIONS
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation
|
COURS
Pour chaque inéquation on considère le demi plan
qui convient (on considère le point origine O (0 ;0) ;
on cherche si il appartient ou pas au demi plan )
La solution graphique du système correspond à tous
les points communs aux deux demi plans (zone non barrée)
Remarques : les droites ” et ” ‘ sont sécantes au point de coordonnées ( 2 ;3) ; Ce point
n’est pas solution du système. ( parce que nous
avons des inégalités strictes)
|
|
Résolution graphique d’un SYSTEME
à 3 INEQUATIONS |
|
Exemple 1:
Résoudre le
système :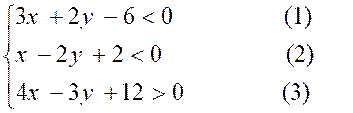
Etant donnés deux axes de coordonnées
« O x » et « O
y » nous allons déterminer dans quelle région du plan se trouvent les
points « M » dont les coordonnées satisfont à ces trois inéquations.
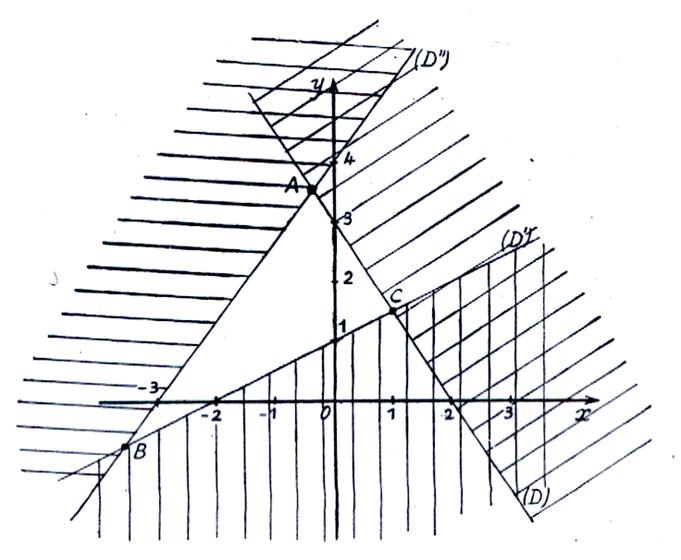
Pour cela construisons les droites qui ont
respectivement pour équations :
(1)
3 x + 2 y - 6 = 0 ( D )
(2)
x - 2 y + 2 = 0 ( D ’ )
(3)
4x - 3y +12 = 0 ( D ’’ )
Pour que l’inéquation (1) soit satisfaite il faut
et il suffit que « M » soit dans la région qui contient l’origine ( car pour « x » = 0 ; « y » = 0
l’inéquation est satisfaite).
Pour que l’inéquation (2) soit satisfaite il faut
et il suffit que « M » soit dans la région qui ne contient pas
l’origine ( car pour « x » = 0 ;
« y » = 0 l’inéquation n’est pas satisfaite).
Enfin pour que l’inéquation (3) soit satisfaite il
faut et il suffit que « M » soit dans la région qui contient
l’origine ( car pour « x » = 0 ;
« y » = 0 l’inéquation est satisfaite).
|
|
Finalement, on voit que « M » doit être à
l’intérieur du triangle ABC formé par les 3 droites (D) ; (D’) ;
(D’’).
Exemple 2 : Résoudre graphiquement.
On désire acheter pour une bibliothèque des romans
de la pléiade (60 € l’un) et des encyclopédies (120€ l’une). On exige les trois
conditions suivantes :
1°) Au moins deux romans.
2°) Plus d’ encyclopédies que de romans.
3°) La dépense doit
être inférieure ou égale à 900 € .
Quelles sont les diverses possibilités
d’achats ?
|
Désignons par « x » le nombre de romans
(nombre entier) et « y » le nombre d’encyclopédies (nombre entier) Les trois contraintes : |
|
D’où : 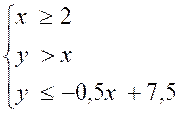
Nous devons tracer les droites ![]() ;
; ![]() ‘ ;
‘ ; ![]() ’’
; telles que
’’
; telles que 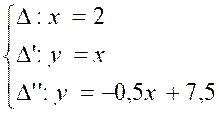
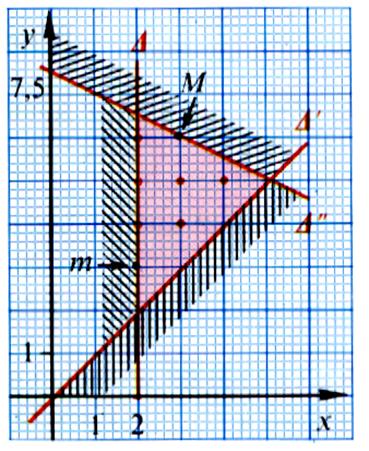
Etude
du graphique :
Le
graphique montre « 8 » solutions répondant au problème.
Remarque :
Le
point « M » (
3 pléiade , 6 encyclopédies) correspond à la dépense maximale de 900 €.
Le
point « m » ( 2 romans , 3 encyclopédies)
correspond à la dépense minimale de 480 €.
RESOLUTION DE PROBLEMES.
Exemple : Un
fabriquant de meubles peut fabriquer
deux modèles de table , « X » et
« Y » , demandant chacun des temps d’usinage et de finition
différents. Son bois lui permet d’usiner 11 tables par jour. Un ouvrier met 3
heures pour usiner une table « X » et
2 heures pour une table « Y ». La personne qui s’occupe des
finitions met 15 mn pour finir une table « X » et 1 heure pour une
table « Y ».
Les quatre ouvriers représentent au total 30 heures
de travail quotidien et la personne qui
s’occupe des finitions travaille 8 heures par jour.
a) Chercher le système d’inéquations
vérifiées par le nombres de tables
« X » et le nombre de tables « Y ».
b) Si le fabriquant veut produire 11 tables par jour, quelles sont ses
possibilités ?
c) Recherchez, parmi les solutions trouvées en « b » si tous les
ouvriers travaillent à temps
complet ?
d) Si une table « Y » est
vendus 10% plus chère qu’une table « X », quelle solution choisira le
fabriquant ?
CONTROLE :
1°) Donner la procédure qui permet de résoudre
« graphiquement » un système d’inéquations du premier degré à deux inconnues.
A) Résoudre le système suivant :
|
|
Corrigé dans le cours. |
B) Résoudre graphiquement les systèmes
d’inéquations suivants :
|
a) |
c) |
|
b) |
d) Que reste - t- il de l’ensemble des solutions si
l’on ajoute l’équation x + y = 1 ? |
C ) Représenter graphiquement l’ensemble des solutions de chacun des systèmes :
|
a) |
b) |
D ) Montrer à l’aide d’un graphique que le système suivant admet une seule
solution entière.
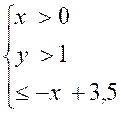
·
Donner cette
solution.
Un fabriquant de meubles peut fabriquer deux modèles de table , « X » et « Y » , demandant
chacun des temps d’usinage et de finition différents. Son bois lui permet
d’usiner 11 tables par jour. Un ouvrier
met 3 heures pour usiner une table « X » et 2 heures pour une
table « Y ». La personne qui s’occupe des finitions met 15 mn pour
finir une table « X » et 1 heure pour une table « Y ».
Les quatre ouvriers représentent au total 30 heures
de travail quotidien et la personne qui
s’occupe des finitions travaille 8 heures par jour.
e) Cherchez le système d’inéquations
vérifiées par le nombres de tables
« X » et le nombre de tables « Y ».
f) Si le fabriquant veut produire 11 tables par jour, quelles sont ses
possibilités ?
g) Recherchez, parmi les solutions trouvées en « b » si tous les
ouvriers travaillent à temps
complet ?
h) Si une table « Y » est
vendue 10% plus chère qu’une table « X », quelle solution choisira le
fabriquant ?
Problème N° 2 : Résoudre graphiquement.
On désire acheter pour une bibliothèque des romans
de la pléiade (60 € l’un) et des encyclopédies (120€ l’une). On exige les trois
conditions suivantes :
1°) Au moins deux romans.
2°) Plus d’ encyclopédie que de romans.
3°) La dépense doit
être inférieure ou égale à 900 € .
Quelles sont les diverses possibilités
d’achats ?
(Voir dans le cours pour le corrigé)