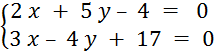|
Info :
Système d’équations (définition) |
||
|
Compétences : -
Savoir transformer
l’équation a x + by + c = 0 en une
équation de la forme : y = …… |
||
|
-
Savoir tracer une
droite d’équation y = a x + b dans un
repère orthonormé. |
|
|
ENVIRONNEMENT du dossier:
|
|
|
|
DOSSIER : Fiches : Les systèmes d’équations. |
|
|
|
|
Les
SYSTEMES d’ EQUATIONS A DEUX INCONNUES. |
|
|
|
<<< retour vers la fiche. |
|
|
|
|
|||
|
|
|
|
||||||
|
|
Fiche 4 : Système de deux équations du premier degré à deux inconnues . |
Info +++ |
|
|||||
|
|
|
|
||||||
|
|
Voici deux équations du premier degré à deux inconnues. |
|
||||||
|
|
« |
« |
|
|||||
|
|
|
|
||||||
|
|
Chacune d’elles possède une infinité de solutions. IL se peut que ces deux équations aient des solutions communes , c’est ce que nous nous proposons de déterminer. |
|
||||||
|
|
|
|
||||||
|
|
·
Procédure : chercher l’ensemble des solutions communes à ces deux
équations : On dit aussi : « résoudre le système d’équations :
|
|
||||||
|
|
|
|
||||||
|
|
Résolution
graphique de ce système d’équations : |
|
||||||
|
|
Dans le plan muni d’un repère , dessinez les
représentations graphiques des équations : « Vous obtenez deux droites. Vous constatez que ces droites se coupent . Lisez les coordonnées du point d’intersection. Vous trouvez ? ………………. |
|
|
|||||
|
|
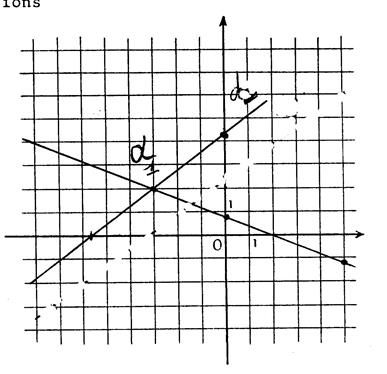
Equation1 :
Si x = 0 ; y = 0,8 ; si y = 0 ; x =
2 ( tracé OK) Equation 2 :
Si x = 0 ; y = 4,25 ; si y
= 0 ; x = - 5,66 Lisez les coordonnées du point d’intersection. Vous trouvez ? ………( -3 ; 2 ) ………. |
…
|
|
|||||
|
|
|
|
|
|||||
|
|
Vérifiez par le calcul que ce couple est solution de chacune des
équations. Ce couple est alors solution du ………………………si
« |
|
||||||
|
|
Démontrons que les droites sont sécantes. Ecrivez les équations de la forme
« |
|
||||||
|
|
« |
Et |
« |
|
||||
|
|
Ont – elle le même coefficient directeur ? NON Donc les droites sont ……………sécantes
…………………………. Elles ont alors un seul point commun. Donc le système possède exactement
une solution. Cette solution est le
couple ( -3… ; 2.) |
|
||||||
|
|
|
|
||||||