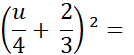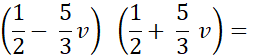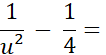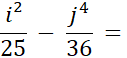Programme de la classe de troisième.	Classe de troisième collège ,
Classe de troisième collège : Fiches sur : Les identités ou les PRODUITS REMARQUABLES .
	Corrigé à faire…….

Pré Requis:

Définition "identité"
Les égalités EG1
Les égalités EG2
Développer
Les éléments et ensembles

Environnement du cours :

warmaths	Objectif précédent Classe de 4^ème : développer.. Classe de 3^ème développer-factoriser,….	Objectif suivant : Les produits remarquables (application newton) Cours de niveau 4 les identités remarquables , utilisation( lycée )	INFO liste des cours proposés
	Ou autre :

	Fiches sur : Les identités ou les PRODUITS REMARQUABLES .
ok	Fiche 1 : Carré d’une somme .
ok	Fiche 2 : Carré d’une différence.
	Fiche 3 : Différence de deux carrés .
	Résumé des 3 fiches
	Fiches 4 : Développer ou factoriser.

TEST

COURS

Devoir contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : carré d’une somme .

Info cours.

Rappel : vous savez développer le produit de deux sommes : · Dans le cas de , on peut écrire ( lire ( 2 x + 3 ) facteur de ( 2 x + 3 )) . On a alors : successivement , Vous avez constaté qu’il y a deux fois le terme «  » . s’écrite ou · ( a + b ) ² = · Puisque “” , il y a donc deux fois le terme «  » ; on écrit alors : «   »

Ce que nous appliquerons aux nombres relatifs.

On retiendra : « a » et « b » étant des nombres relatifs : ( a + b ) ² = a² + 2ab + b²

( terme ? , facteur ?)

Ce que l’on traduit par : Le carré d’une somme de deux nombres est égale à la somme du carré du premier terme , du double produit des deux nombres et du carré du deuxième terme.

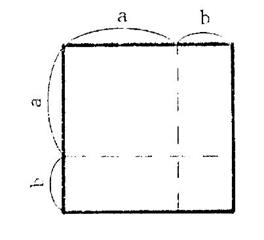
Interprétation géométrique : ( dans le cas où « a » et « b » sont des nombres positifs )

Voir ci-contre : Le dessin représente un carré dont la mesure de la longueur du côté est «  . .. + . …… » La mesure de son aire est donc égale à :

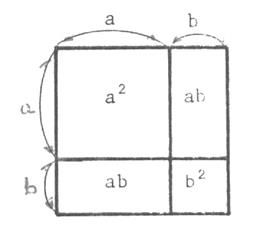
Voir ci-contre : Le dessin représente le même carré ,mais partagé en « 4 » surfaces dont la somme des mesures des aires est : « …. » On a bien donc : …….. = . …. + 2 . … + . …..

Remarque 1 : Quand on remplace ( a + b )² par a² + 2 ab + b² , on dit que l’on développe. Quand on remplace a² + 2 ab + b²  par ( a + b )² on dit que l’on factorise .

Remarque 2 : Désormais pour développer le carré d’une somme , vous ne devez plus effectuer les calculs comme on l’a fait précédemment , mais il vous faut utiliser la formule ..

Exemple : on vous demande de développer : = ( carré de « 5y ») + ( double produit ) + ( carré de « 7 »)

Activités : Développer ( les lettres représentent des nombres quelconques )

Attention : Sachant que « a = 3 » et « b = 7 » Calculez ( a + b ) ² = ( . … + ….. )² = . …. = …… et calculez «  a² + b² » = …. ² + . ….. ² = . … + . … = . …. Vous constatez donc que , en général , Attention donc , quand vous développez , n’oubliez pas le « . ……….. » .

Exercice 2 : Complétez de telle sorte que le premier membre de l’égalité soit le développement du carré d’une somme .

«

v On se propose de factoriser :

On remarque qu’il existe une certaine analogie entre «   » et «   » Cherchons quel nombre peut jouer le rôle de « a » et quel nombre peut jouer le rôle de « b ».

Exercice 3 : Faites de même pour :

Attention : Dites en l’expliquant si vous pouvez factoriser «   » par la méthode précédente .

Calcul mental : Pour calculer «  31 ² » , on pense à «  31 = 30 + 1 » 31 ² = ( 30 + 1 )² = 30 ² + 2 fois 30 fois1 + 1 = 900 + 60 + 1 v Calculez mental : 41² ; 52² ; 103 ² ; 10,1²

Fiche 2 : Carré d’une différence.

Info Cours.

Développez . On peut écrire que ) . On a alors : )

· De même =

Ce que nous appliquerons aux nombres relatifs.

On retiendra : « a » et « b » étant des nombres relatifs :

Activités : Développez :

Exercice 2 : Complétez de telle sorte que le premier membre de l’égalité soit le développement du carré d’une différence.

Exercice 3 : « Factorisez »

Calcul mental :

Pour calculer , on pense que

Calculez mentalement : 29² ; 48 ² , 0,99² ; 1,9 ²

Fiche 3 : Différence de deux carrés .

Info cours

Développez : et après simplification

Or : et

On peut donc écrire

Cas général : Développez

Et après simplification :

Remarque : quand on remplace par , on dit que l’on «  développe ».

On retiendra : « a » et « b » étant des nombres relatifs :

Exercices série 1 : Développez en utilisant la formule précédente.

v L’égalité : peut s’écrire aussi : ……………….

A retenir :

Théorème : La différence des carrés de deux nombres est égale au produit de leur somme par leur différence. ( les nombres étant écrits dans le même ordre que leurs carrés ).

Remarque : Quand on remplace par , on dit que l’on « factorise ».

v On vous demande de factoriser : 25 x² - 9 , vous remarquez que et

Vous pouvez donc écrire que

Exercices ( série 2 ) : Factorisez comme précédemment .

v On vous demande de factoriser : A = ( 5 x – 3 )² - ( 3 x + 4 )² Vous remarquez que ( 5 x – 3 )² - ( 3 x + 4 )² se présente sous la forme «  a² - b² » dans laquelle ( 5 x – 3 ) joue le rôle de « a » et ( 3 x + 4 ) joue le rôle de « b ».

On a alors : =

En supprimant les parenthèses on a : A =  ; soit A = Et après simplification  ……………….

Activité : (série 3 ) : Factorisez comme précédemment ( les lettres représentent des nombres )

Calcul mental :

Pour calculez , on pense que «  31 = 30 +1 » et « 29 = 30 -1 » Donc :

Résumé des 3 fiches :

Remarques :

Fiches 4 : Développer ou factoriser. Et « identités remarquables »

« Développer » et « factoriser » sont des opérations inverses l’une de l’autre. Complétez les égalités ci-dessous. Ces égalités ( 9 ) correspondent aux différentes situations que vous pouvez rencontrer.

( 1 )

( 6 )

( 2 )

Et trop difficile à savoir faire en classe 3^ème collège.

( 3 )

( 4 )

( 7 ) .

( 5 )

( 8 ) ….

( 9 ) …..

Remarque 1 : ( a + b ) ² est un produit de facteurs . C’est le produit de ( . ……. ) par ( . …….. ) · Quand dans un calcul , on vous demande de développer , ( ou de factoriser) , vous cherchez parmi les égalités ci-dessus , celle dont le membre de gauche correspond à ce qui est donné dans l’énoncé et vous transformez celui-ci conformément au membre de droite.

Exemple 1 : Développons «  A = ( 7 x + 5 ) ( 7 x – 5 ) »

On peut penser que l’on est dans la situation de l’égalité ( 2 ) , mais en regardant de plus prés , on s’aperçoit qu’il s’agit plutôt de l’égalité (5) On a alors (7x) ² - ( 5) ²

Exemple 2 : Factorisons : B = ( x + 4 ) ² - 2 ( 3x – 5 ) ( x + 4 ) + ( 3 x – 5 )² On peut penser que l’ on est dans la situation de ‘égalité (6 ) car on voit un facteur commun à 2 termes , mais ce facteur ne se retrouve pas dans le troisième. En regardant de plus près , on s’aperçoit qu’il s’agit plutôt de l’égalité ( . … ) : . ………. Dans laquelle « a = . ………. » et «  b = . ……….. » . ON a alors «  B =  » On enlève les parenthèses : «  B =  » ; «  B =  »

Remarque 2 : Après avoir développé , on obtient une somme de …………………. Après avoir factorisé , on obtient un …………………………….de Dans tous les cas où c’est possible , on réduit les termes semblables .

Exercice 3 : Développez en utilisant les produits remarquables et réduis.

C =

21 / 01 / 2016