Pré requis
|
|
|
|
|
ENVIRONNEMENT du dossier :
|
Notions : |
Classement « Suite » |
Tableau
|
||
|
« |
||||
|
|
|
|||
DOSSIER : COMPARAISON DES
FRACTIONS à L’UNITE « 1 »
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rappel :Comment reconnaître un nombre décimale ?:
un nombre décimal est un
alignement horizontal de chiffre (s) séparé ou non par une virgule. ( 0, 5 ;
1 ; 1,25
sont des nombres décimaux ; ils
sont toujours séparés par des points virgules)
La fraction peut être inférieure ; égale ;
ou supérieure à l’unité « 1 »
Activité : On choisit pour
« unité » un pain de mie pré
tranché ( ou un
pain d’épice )
|
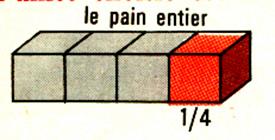
1er cas : la fraction est inférieure à l’unité ( le nombre
décimal est inférieur à « 1 ») |
|
|
« chaque matin , je mange un quart ( l’écriture
« |
|
|
Constat : le numérateur est « plus petit que » le
dénominateur : Donc « Remarque : Pour éviter l’écriture de phrase inutile : « |
|
|
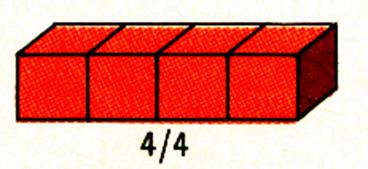
2ème cas :
la fraction est égale à l’unité ( le nombre décimal est égal à « 1 ») |
|
|
« En quatre jours , je mange les quatre
quarts ( ou le pain entier . l’écriture
« |
|
|
Constat : le numérateur est égal au dénominateur : Donc « |
|
|
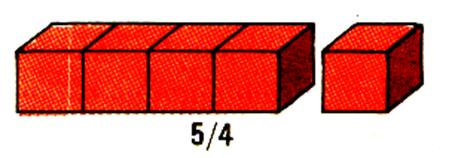
3ème cas : la
fraction est supérieure à l’unité ( le nombre
décimal à une valeur supérieure à « 1 ») |
|
|
« En 5 jours , je mange cinq quarts ( ou le pain entier . l’écriture
« |
|
|
Constat : le numérateur est égal au dénominateur : Donc « Remarque : Pour éviter l’écriture de phrase inutile : « |
|
Extraction
des nombres entiers d’une fraction :
exemple :
![]() h = 2 h et
h = 2 h et ![]() (
voir la division 9 : 4
= 2 et il reste 1 )
(
voir la division 9 : 4
= 2 et il reste 1 )
Pour
extraire les unités contenues dans une
fraction plus grande que 1 , on divise le numérateur
par le dénominateur .
( pour en savoir plus : voir la
division euclidienne)
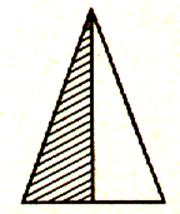
On peut exprimer par une fraction
la surface des figures suivantes
:
Quelle fraction d’aire représente la partie hachurée ?:
hachurées couvre la moitié de l’aire
totale (A) . ( 0,5 A)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX AUTO - FORMATIFS
1°) Comment reconnaît – on qu’une fraction est « inférieure à 1 » ? ;
« égale à 1 » ? ; « supérieure à
1 » ?
2°) Traduire :
![]() < 1 ; «
< 1 ; « ![]() » = 1 ;
» = 1 ;
![]() > 1
> 1
3°) Comment fait – on pour extraire des unités d’une fraction
plus grande que 1 ?
.
EVALUATION
1°)
Classer les fractions suivantes en 3 groupes :a) celles plus petites que
1 ; b) celles égales à 1 ; celles plus grandes que 1
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2°)
Classer ces fractions de la plus grande à la plus petite ,
encadrer celles qui sont égales à l’unité.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3°) a)
A ![]() m il manque
m il manque ![]() pour faire un mètre .
pour faire un mètre .
b)
Les ![]() du litre de lait sont
bus ; il reste
du litre de lait sont
bus ; il reste ![]() de litre.
de litre.
c)
![]() du jardin ne sont pas bêchés . J’ai
donc bêché
du jardin ne sont pas bêchés . J’ai
donc bêché ![]() du jardin
du jardin
4°)
Ecrire des fractions plus petites que 1 : ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
5°)
Ecrire des fractions plus grandes que 1 : ![]() ;
; ![]() ;
; ![]() ;
; ![]()
6°)
Extraction des nombres entiers :
![]() ;
;![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]()