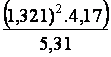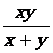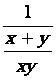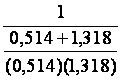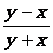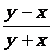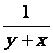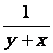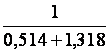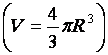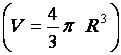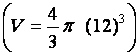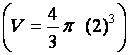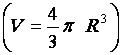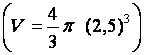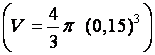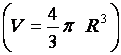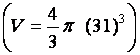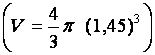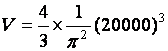Pré requis :
|
|
|
|
|
|
précédent : Nomenclature généralités |
Complément d’informations : |
||
|
Informations suivantes : Liste des
objectifs avec les nombres décimaux |
Calculs numériques . Fiche 1
|
|
|||||||
|
|
|
||||||
|
Consigne : Calculs à effectuer directement à la
machine. |
Réponses |
||||||
|
|
|
12,978 |
|||||
|
1.
|
1, 415 + 7,212 + 0,051
+ 4,3 |
|
|||||
|
|
|
|
|||||
|
2.
|
1,515 – 2,312 – 6,31 +
7,189 |
0,082 |
|||||
|
|
|
|
|||||
|
3.
|
|
1,3704 |
|||||
|
|
Info : puissances |
|
|||||
|
4.
|
Calculer les six
premières puissances de 1,414. |
(1,414.)1 =
1,414. ; (1,414.)2 =
1,999 396 ; (1,414.)3
|
|||||
|
|
|
(1,414.)4
(1,414.)6
|
|||||
|
|
|
|
|||||
|
5.
|
Calculer les six
premières puissances de 1,732 |
(1,732.)1 = 1, 732
; (1,732.)2 = 2,999
824 ; (1,732.)3 |
|||||
|
|
|
(1,732.)4
(1,732.)6
|
|||||
|
6.
|
Calculer pour « x
= 0,514 » et « y = 1,318 » les expressions suivantes : |
|
|||||
|
|
« x² + y² » |
« 0,514²
+ 1,318 ² »= + 2 ,
001 320 |
|||||
|
|
« x² - y ² » |
«0,514 ² -
1,318 ² » = - 1, 4 72 928 |
|||||
|
|
|
||||||
|
7.
|
Calculer pour « x
= 0,514 » et « y = 1,318 » les expressions suivantes : |
« x =
0,514 » et « y = 1,318 » |
|||||
|
|
« 4 x y3
– 3 x » |
« 4
(0,514)( 1,318 3) – 3 (0,514) » |
|||||
|
|
« (1 + x +
y )² – x ² » ? est de la
forme : (A + B )( A-B) |
Sol. 1 :
« (1 + 0,514 + 1,318 )² – 0,514 ² » |
|||||
|
|
|
||||||
|
|
On pourrait
développer mais : (1 + x +
y) (1 + x + y) =
1 + x + xy +x + x² + xy + y + xy + y² = 1 + 2 x + 3 xy + x² + y² = ça ne mène à rien !! |
|
|||||
|
|
S
2 : « (1 + x +
y ) + x ) (
(1 + x + y ) -
x ) = (1 + 2x +
y ) (1 + y ) |
S
2 : «(1 + 2x +
y ) (1 + y ) » = (1 +
2 (0,514) + 1,318)
(1 + 1,318 ) |
|||||
|
|
|
S
2 = 7,756 028 |
|||||
|
|
|
||||||
|
8.
|
Calculer pour « x
= 0,514 » et « y = 1,318 » les expressions suivantes : |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
9.
|
Calculer pour « x
= 0,514 » et « y = 1,318 » les expressions suivantes : |
« x =
0,514 » et « y = 1,318 » |
|||||
|
|
3 ( x + y )² - 14 x |
3 ( 0,514 +
1,318 )² - 14 (0,514) = 2,872 672 |
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
10. |
Calculer pour « x
= 3 , 519 » et « y = 0,591 » les expressions suivantes : |
|
|||||
|
|
« x² - y² » |
|
|||||
|
|
« x² + y² » |
|
|||||
|
|
« 4 x y3
– 3 x » |
|
|||||
|
|
« (1 + x +
y )² – x ² » |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
3 ( x + y )² - 14
x |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
11. |
Calculer pour « x
= - 3 , 78 » et « y = - 2 , 47 » les expressions
suivantes : |
|
|||||
|
|
« x² - y² » |
|
|||||
|
|
« x² + y² » |
|
|||||
|
|
« 4 x y3
– 3 x » |
|
|||||
|
|
« (1 + x +
y )² – x ² » |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
3 ( x + y )² - 14
x |
|
|||||
|
|
|
|
|||||
|
|
|
||||||
|
12. |
Déterminer le plus
petit entier « n » tel que ( 1 + x )n dépasse « 2 » avec « x =
0,3 » et « x = 0,4 » |
·
Pour « x = 0,3 » ( 1,3 ) 2
= 1,69 < 2
; ( 1,3 ) 3 =
2,197 > 2 Donc pour
« x = 0,3 » ; « n= 3 » ·
Pour « x = 0,4 » ( 1,4 ) 2
= 1,96 < 2
; ( 1,4 ) 3 =
2,744 > 2 Donc pour
« x = 0,4 » ; « n= 3 » |
|||||
|
|
|
||||||
|
13. |
Déterminer le plus
petit entier « n » tel que ( 1 + x )n dépasse « 2 » avec « x =
0,15 » et « x = 0,2 » |
·
Pour « x = 0,15 » ( 1,15 ) 2
= 1,322 5 < 2
; ( 1,15 ) 3 =
1,520 875 < 2 ( 1,15 ) 4
= 1,749 006 2 <
2 ; ( 1,15 ) 5 Donc pour « x = 0,15 » , « n =
5 » ·
Pour « x = 0,2 » ( 1,2 ) 2
= 1,44 <
2 ; ( 1,2 ) 3
= 1,728 < 2 ; ( 1,2 ) 4 = 2, 073 6
> 2 Donc pour
« x = 0,2 » ; « n= 4 » |
|||||
|
|
|
||||||
|
14. |
Déterminer le plus
petit entier « n » tel que ( 1 + x )n dépasse « 2 » avec « x =
0,1 » et « x = 0,12 » |
Pour « x
= 0,1 » ( 1,1 ) 2
= 1,21 ( 1,1 ) 3
= 1,331 ( 1,1 ) 4
= 1,464 1 |
|||||
|
|
|
||||||
|
15. |
Déterminer le plus petit
entier « n » tel que ( 1 + x )n dépasse « 2 » avec « x =
0,05 » et « x = 0,07 » |
Pour « x
= 0,05 » ( 1,05 ) 14
Donc pour
« x = 0,05 » ; « n= 15 » Pour « x
= 0,07 » ( 1,07 ) 10
Donc pour
« x = 0,07 » ; « n= 11 » |
|||||
|
|
|
||||||
|
16. |
Déterminer le volume
d’une sphère |
·
Calcul de « V » , en centimètres cubes , pour R = 12 cm
V ·
Calcul de « V » , en centimètres cubes , pour R = 2 m
V |
|||||
|
|
|
||||||
|
17. |
Déterminer le volume d’une sphère |
·
Calcul de « V » , en centimètres cubes , pour R = 2,5 cm
V ·
Calcul de « V » , en centimètres cubes , pour R = 0,15 cm
V |
|||||
|
|
|
||||||
|
18. |
Déterminer le volume
d’une sphère |
·
Calcul de « V » , en mètres cubes , pour R = 31 m
V ·
Calcul de « V » , en mètres cubes , pour R = 1,45 m
V |
|||||
|
|
|
||||||
|
19. |
Déterminer le volume
d’une sphère avec
2 |
V V |
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||