|
Pré requis |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Avant : |
Après : |
Listes :
|
|
|
2. -les
pourcentages et intérêts |
|||
INTÊRETS
COMPOSES : ACTUALISATION
Chapitres :
|
|
1.
PRINCIPE DES INTERETS COMPOSES |
|
|
|
2. CALCULS RELATIFS
AUX INTERÊTS COMPOSES |
|
|
|
3. ACTUALISATION D'
UN CAPITAL |
|
|
|
4. TAUX EQUIVALENTS |
|
|
|
5. ESCOMPTE
A INTÊRETS COMPOSES |
|
- PRINCIPE DES
INTERETS COMPOSES
On considère un capital de C0 =30 000 € ,
déposé dans une banque le 1er Janvier 2011 au
taux annuel de t = 7,5 %.
Les intérêts produits I pendant l'année 2011 ( n
= 1 an )sont donc
![]()
soit : I = 2250 €
La valeur acquise (VA) par le capital C
au bout d'un an est donc
VA
= C + I = 30000 + 2250 =32250 €
En résumé le nouveau capital au bout d'un an C1
a été calculé de la manière suivante :
C1 = VA = C + I =
30 000 + 30 000´0,075 = 30 000´1,075
En 2012 ce sera donc C1 qui servira
au calcul des intérêts (les intérêts sont capitalisés c'est à dire ajouté au
capital de départ) :
La valeur acquise pour 2012 est donc C2
= C1´1,075 = 30 000 ´ 1,0752
En
2013 : C3 = 30 000 ´ 1,0753………………..
On remarque que
pour calculer la valeur acquise Cn par le capital au bout de n périodes, il
suffit de considérer une suite géométrique Cn de raison q = 1,075 et
de premier terme C0 = 30 000.
Ainsi : En
2010 : C0 = 30 000
En
2011 : C1 = 30 000 ´ 1,075
En
2012 : C2 = 30 000 ´ 1,0752
En
2013 : C3 = 30 000 ´ 1,0753
En
résumé :
Si un capital C est placé, à intérêts composés,
pendant n périodes, au taux périodique t, alors la valeur acquise Cn
et l'intérêt produit I sont donnés par les relations :
![]()
- CALCULS
RELATIFS AUX INTERÊTS COMPOSES
Calcul
de C connaissant Cn, t et n
Il
faut transformer la relation précédente qui devient : 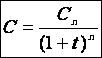
Exemple
: Placé à intérêts composés pendant
6 ans, au taux annuel de 8 %, un capital a acquis la valeur de 19 042,50 € ,
Quel est ce capital ?
 €
€
Calcul
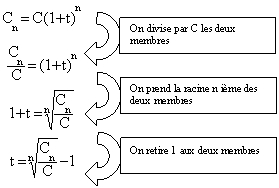
du taux d'intérêt « t »
Il faut transformer la formule ![]()
Voici les étapes de cette transformation :
Exemple Un capital de 50 000 € placé à intérêts composés pendant 14 ans au
taux annuel « t » a acquis une
valeur de 178 142,55 € . Calculer
« t ».
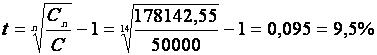
Calcul
du nombre de périodes « n »
Il faut transformer la formule ![]()
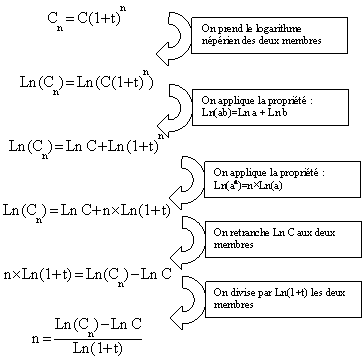
Voici les étapes de
cette transformation :
Exemple : Combien faut-il d'années de
placement à intérêts composés pour qu'un capital de 8000 € acquiert la valeur de 11 220,41 € au taux de 7 % l'an.
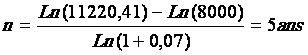
- ACTUALISATION
D' UN CAPITAL
Il s'agit
de répondre à la question : Quelle est la valeur au 1er janvier 2005
d'un capital ayant une valeur de 10 000 €
au 1er janvier 2010 placé au taux annuel de 8 %?
Il
faut donc calculer C connaissant Cn, t et n on applique donc :
D'où 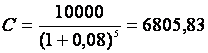
4. TAUX EQUIVALENTS
Définition Des taux relatifs à des
périodes de capitalisation différentes sont dits équivalents si, appliqués à
des capitaux égaux pendant des durées égales ils donnent des valeurs acquises
égales.
Un capital
de 10 000 € placé à intérêt composés pendant deux ans au
taux annuel de 6 % prend la valeur : C2 = 10000(1+0,06)2
= 11236 €
Un
capital de 10 000 € placé à intérêts
composés pendant 2 ans aux taux semestriel de 3 % prend la valeur C4
= 10 000(1+0,03)4 = 11255,09 €
Bien
que les taux soient proportionnels, les valeurs acquises sont différentes.
On va
donc chercher quel taux semestriel t-il faut avoir pour que les valeurs
acquises par les deux placements sur 2 ans (4 semestres) soient égales On doit
donc résoudre l'équation :

Donc t =
0,0296 (arrondi à 0,0001 près) soit 2,96 %
Conclusion : Le taux annuel de 6 % et le taux
semestriel de 2,96 % sont des taux équivalents.
5.
ESCOMPTE A INTÊRETS
COMPOSES
On désire actualiser une créance ( un crédit par exemple) de
20 000 € arrivant à échéance dans 5 ans.
L'emprunteur désire rembourser ce crédit maintenant, la taux
annuel d'escompte est alors de 11 %.
Il faut calculer la valeur actuelle de cette créance soit :
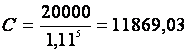
L'emprunteur remboursera donc la somme de 11869,03 €
Equivalence de deux capitaux
Définition Deux capitaux placés à
intérêts composés( au même taux) sont équivalents à une date donnée, si à cette
date, ils ont la même valeur actuelle. Ils sont alors équivalents à toute autre
date
Exemple Considérons deux capitaux : l'un de 10
000 € à échéence dans 3 ans, l'autre de 12 544 € à échéance dans 5 ans. Le taux
annuel est de 12 %.
On calcule leur valeur actuelle :
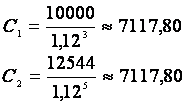
Ces deux capitaux ayant aujourd'hui la même valeur actuelle
sont dits équivalents. Dans un an il auront la même valeur actuelle : 7 117,80 ´ 1,12 = 7 971,94 €
Echéance commune et échéance moyenne
Définition Un effet escompté à intérêts
composés est équivalent à plusieurs effets à une date donnée, si à cette date,
sa valeur actuelle est la somme des valeurs actuelles des autres effets.
L'échéance commune et l'échéance moyenne ne dépendent pas de la date
d'équivalence. L'échéance moyenne dépend du taux.
On veut remplacer trois réglements, le premier de 15 000
€ à échéance dans 3 ans, le deuxième de
21 000 € à échéance dans 4 ans, le troisième de 30 000 € à échéance dans 6 ans,
par un règlement unique de 70 000 €.
Quelle doit être l'échéance (échéance commune) du nouvel
effet pour qu'il soit équivalent à la somme des trois autres ? Le taux annuel d'escompte
est de 11 %
On appelle n ( en année) l'échéance du nouvel effet, on écrit
alors que la valeur actuelle du nouvel effet est égal à la somme des valeurs
actuelles des trois effets et on résout l'équation pour trouver n :

L'échéance commune est donc 5 ans 59 jours.
On reprend l'exemple précédent, mais maintenant on va
calculer l'écéance m qui correspond à un règlement unique de 66 000 € (somme
des valeurs des trois effets) :

L'échéance moyenne est donc : 4 ans 216 jours environ