|
Addition avec des nombres entiers et décimaux |
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : 1°) La longueur : |
Objectif
suivant : |
||||
|
|
|||||
|
|
DOSSIER : Addition de longueurs (segments) |
|
|||
|
|
·
Somme de
deux ou plusieurs longueurs
|
|
|||
|
|
·
PROPRIETES
d’une SOMME
|
|
|||
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
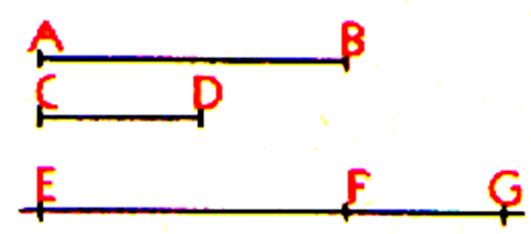
Si après avoir découpé un rouleau de papier de longueur donné en
plusieurs morceaux ,
nous voulons reconstituer le rouleau dans sa totalité , nous porterons bout à
bout les morceaux précédemment coupés.
Exemple :
|
|
En mettant bout à bout AB ; BC ; CD ;
DE ; EF on obtient AF
Somme de deux ou plusieurs longueurs
On appelle « somme de deux ou
plusieurs longueurs , la longueur obtenue en portant
sur une même droite illimitée et à la
suite les unes des autres des longueurs
respectivement égales au longueur données.
|
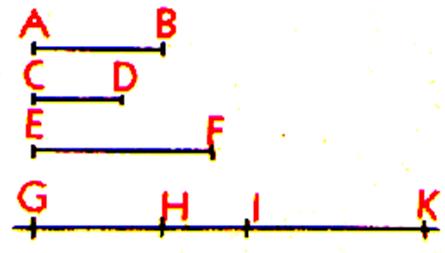
Premier cas |
|
|
Somme de deux longueurs : si EF = AB et FG = CD , le segment EG représente la somme des segments AB et
CD. On écrit EG = AB + CD |
|
|
Deuxième cas : |
|
|
Somme de plusieurs longueurs : Si GH = AB ; HI =
CD ; IK =EF Le segment GK est la somme des segments AB ,
CD et EK : On écrit GK = AB + CD + EF |
|
PROPRIETES d’une SOMME
|
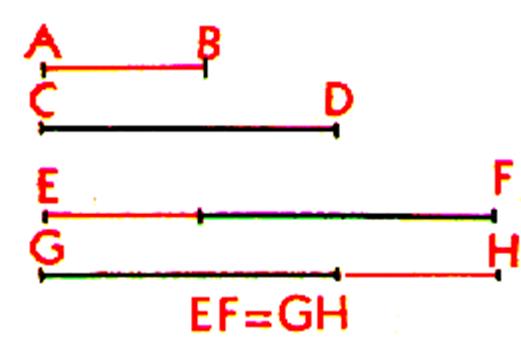
Première propriété |
|
|
La somme de deux ou plusieurs longueurs ne dépend pas de l’ordre
suivant lequel ces longueurs sont données. AB + CD = EF ou AB + CD = GH De toute façon : EF = GH |
|
|
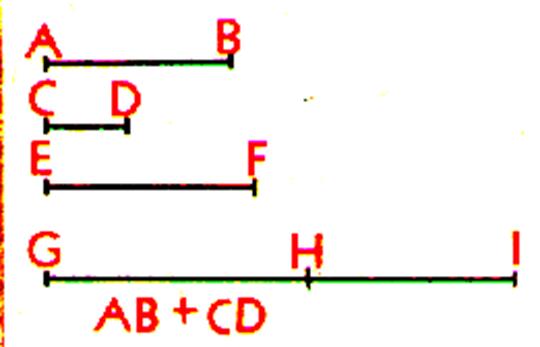
Deuxième propriété |
|
|
La somme de plusieurs longueurs
ne change pas quand on
remplace certaines d’entre elles par
leur somme effectuée . Remplaçons les segments EF et CD par leur somme effectuée GH et
faisons ensuite la somme des segments GH et AB ,
nous obtenons le même résultat qu’en
portant à la suite les uns des autres , les segments AB , CD , puis EF |
|
L’
ADDITION :
L’addition est l’opération qui permet
de trouver une somme
Pour
trouver la somme des longueurs de deux morceaux de ruban mesurant
|
|
|
|
|
|
TRAVAUX
AUTO FORMATIFS. |
|
|
|
|
|
|
|
EVALUATION 1°) trouver la somme des longueurs de
deux morceaux de ruban mesurant 2 °) ajouter : 5,29 m ; 3,17 dam et 25,8m 12,7 hm 132 dam et |
|
|
|
|
|
|
|
|
|