|
Module :
Géométrie |
DOSSIER : 134 |
||||
|
LOGICIEL warmaths Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
|||||
|
TRAVAUX FORMATIFS COLLEGE /Lycée Matière : MATHEMATIQUES. Niveau VI |
. |
||||
|
LE TRAPEZE ( caractéristiques) |
|||||
|
Informations à consulter éventuellement : Info 1 @ cours : les trapèzes . Info 2 @ cours niveau V : les polygones
usuels (surfaces de base) . |
|||||
|
|
|||||
|
TRAVAUX CONTROLE |
|||||
|
Les
questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. |
|||||
|
|
|||||
|
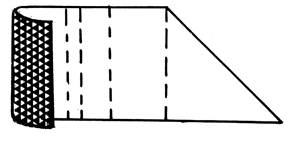
1.Coupez
une bande régulière, selon des droites non parallèles vous obtenez des
quadrilatères qu’on nomme des trapèzes. |
|||||
|
Un
trapèze a deux côtés parallèles et inégaux, qu’on appelle les bases du
trapèze; AB est la petite base, DC la grande base. La
distance entre les bases est la hauteur du trapèze. On la mesure souvent en
partant d’un sommet c’est la perpendiculaire à la base opposée (AH). |
|
||||
|
|
|||||
|
|
Avec
un côté (MP) perpendiculaire aux bases, le trapèze MNOP est remarquable; on l’appelle
trapèze rectangle il a deux angles
droits, et le côté MP, égal à la hauteur, permet de la mesurer
directement. |
||||
|
TRAVAUX : EVALUATION 2 - Activité : |
|||||
|
|
a) ) Tracez, à l’aide du double-décimètre et de l’équerre,
un trapèze rectangle de b) A l’aide de l’équerre, dessinez plusieurs fois
la hauteur; puis faites glisser sur ces traits
le côté perpendiculaire aux bases, afin de
vérifier qu’ils sont tous égaux. |
||||
|
3. Découpez, dans des papiers
de couleurs différentes, deux trapèzes rectangles mesurant 4. Tracez deux lignes droites parallèles, distantes
de |
|||||
|
|
5. Reproduisez le triangle ABC, avec les dimensions suivantes AB = Par
le milieu M de BC, menez la parallèle MN à AC; nommez le trapèze ainsi
obtenu; mesurez sa petite base que remarquez-vous, par rapport à AC ? Tracez
MP parallèle à AB; comparez MP à AB. |
||||
|
6
Tracez un triangle isocèle de
base AB et de sommet M. Par un point quelconque de MA, menez une parallèle CD
à AB. Désignez les deux figures obtenues, et nommez- les. Mesurez les côtés CA
et DB. Que remarquez-vous ? On dit que CDBA est un trapèze isocèle. |
|||||
|
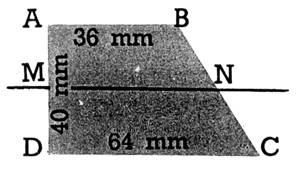
7 Reproduisez le trapèze ci-contre, selon
les cotes exactes. Tracez MN, M étant
le milieu de AD, N le milieu de BC. Mesurez MN, et comparez la mesure à celle
de la somme AB + DC. Que remarquez-vous? |
|
||||