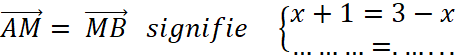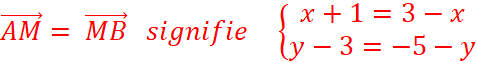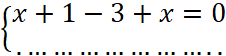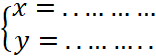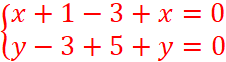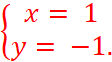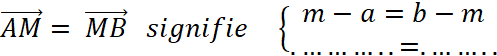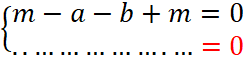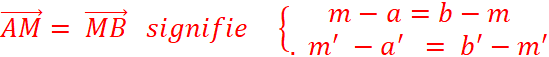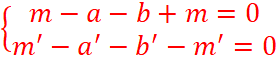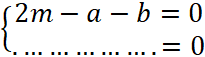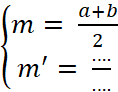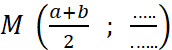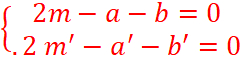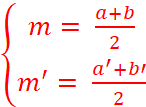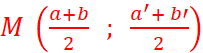Fiches 3^ème :        « Coordonnées du milieu d’un segment »  et   « vecteurs »   et couple de points.

Fiche 1 : Coordonnées d’un vecteur.  Voir la fiche ….

Fiche : Calculs des  coordonnées du milieu d’un segment .

déjà vu : Le milieu d’un segment.

Fiche ( 3^ème ) : Coordonnées du milieu d’un segment .

 ( voir la fiche 3 @ )

Co

Placez les points  et  .

Placez le point « M » milieu de .

Vous lisez :   

Calculons les coordonnées de « M ».

Appelons – les :  

« M » est le milieu de . Signifie que

 ; 

 ; 

C'est-à-dire :         d’où      donc   

C'est-à-dire :         d’où      donc   

Cas général :

Dans le plan muni d’un repère , considérons les points    et  .

Calculons le couple des coordonnées de « » milieu de .        Appelons –le  .

« M » est le milieu de  signifie que  .        ;

« M » est le milieu de  signifie que  .        ;

     c’est  à dire  

     c’est  à dire  

Ce qui s’écrit        d’où       ; 

Ce qui s’écrit        d’où       ;   

Théorème :

Dans le plan relativement à un repère , pour tout segment,

-          l’abscisse du milieu est égale à la demi-somme des abscisses des extrémités.

-          l’ordonnée  du milieu est égale à la demi-somme des ordonnées des extrémités.

Activité 1 :

Déterminez les coordonnées de « G » milieu de .

Sachant que   E ( 8 ; - 3 )  et F ( - 2 ; 5 ) .                                  «  G ( …… ; …….) »

Activité 2 :

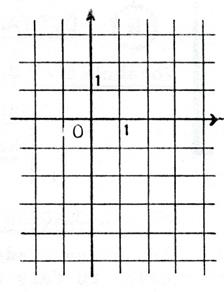
Placez les points    et .

« L » est le symétrique de « K » par rapport à « N ».

Placez « L »  et lisez ses coordonnées .

Déterminons les coordonnées de « L » par le calcul.

« L » est le symétrique de « K » par rapport à « N » , cela signifie que  « N » est le milieu de .

Nous appelons ( x ; y ) le couple de coordonnées de « L ».

Grâce au théorème précédent , on peut écrire :

    et   ;  A vous de continuer si la solution est effacée…

    et   ;  soit     et      donc 

Activité 3 :

1°) Soit « M » le milieu de  . Placez « M ». Calculez ses coordonnées .  «  M ( …. ; …..)

2°) Placez le point « D » tel que « ABCD » soit un parallélogramme.  «   D ( … ;…..) .

3°) Vous allez calculer les coordonnées de « D ».

« ABCD » est un parallélogramme signifie que   et  ont même   milieu .

Donc « M » est le milieu de ………………………………

Appelons   ( x ; y ) les coordonnées de « D » .

Grâce au théorème précédent  , on a :

  et      . Continuez .

4°)  Calculez de même les coordonnées de « E » tel que « ABEC »  soit un parallélogramme .   E ( …. ; ….) et les coordonnées de « F » tel que « AFBC » soit un parallélogramme .  F ( …… ; …..)

Complétez la figure . ( Faîtes les calculs  sur une feuille à part …….)

Le corrigé de cette activité  n’existe pas encore……( 5 / 10 / 2015 ) ……….