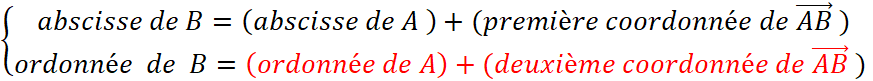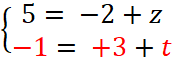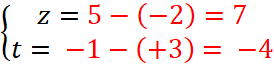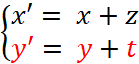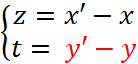|
|
Classe de 3ème collège. |
|||
|
MATHEMATIQUES |
|
|
||
|
|
|
|
||
|
DOSSIER : LES VECTEURS : |
||||
|
Point : Pré requis : ce qu’est un point..................) |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : Plan , ligne , point : généralités Pré requis : Fiche 1 :
Coordonnées d’un vecteur. Voir la
fiche …. |
Objectif
suivant : |
|
|
|
Fiches 3ème : « Coordonnées » et
« vecteurs » et couple de
points. |
|
|
|
|
|
|
|
Fiche 1 : Coordonnées d’un vecteur. Voir
la fiche …. |
|
|
|
|
|
|
|
Fiche 2 : Coordonnées d’un vecteur défini
par un couple de points. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fiche 1 : Coordonnées d’un
vecteur. |
|
|||
|
|
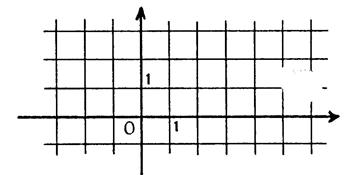
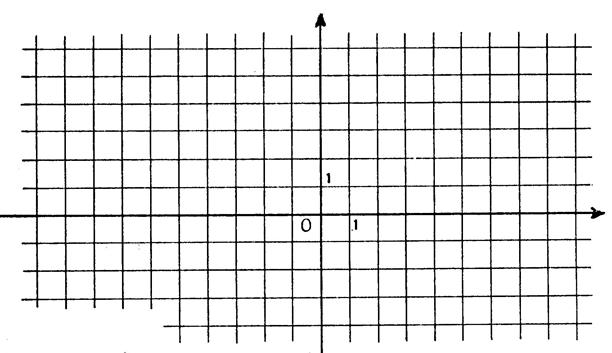
Vocabulaire : On appelle : « repère du plan deux axes
de coordonnées de même origine » . On dit souvent : Le plan est muni
d’un repère d’origine « O ». Cela
signifie : «
On a choisi dans le plan deux axes de coordonnées d’origine
« O » ». |
|
|||
|
|
|
||||
|
|
Fiche 2 : Coordonnées d’un vecteur défini par
un couple de points. |
|
|
||
|
|
|
|
|||
|
|
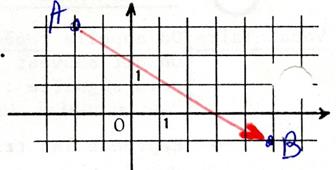
Placez les points A ( -2 ; 3)
et B ( 5 ; -1). Lisez les coordonnées de Calculons le couple de
coordonnées de |
|
|
||
|
|
|
On descend de 4 cases soit :( - 4)
On se déplace de
gauche à droite de 7 cases soit : +7 |
|
||
|
|
On peut considérer que
le point « B » est l’image du point « A » dans la
translation du vecteur Grâce au théorème de la
fiche ( « 5
« @..) sur la translation , on peut
écrire : |
|
|||
|
|
|
|
|||
|
|
Donc : En appelant ( z , t ) le couple de coordonnées du vecteur |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Cas général : Dans le plan muni d’un repère , considérons les points « Nous allons calculer le
couple de coordonnées de |
|
|||
|
|
Le point
« B » est l’image du point « A » dans la translation du
vecteur |
|
|||
|
|
|
|
|||
|
|
D’où le théorème : |
|
|||
|
|
Dans le plan muni d’un repère
, si |
|
|||
|
|
|
|
|||
|
|
Activité 1 : Déterminez les
coordonnées du Vous trouvez : |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Activité 2 : |
|
|||
|
|
Appelons ( x ; y ) , le
couple de coordonnées de « H ». On a alors
|
|
|||
|
|
Activité 3 : |
|
|||
|
|
Placez ces points. Démontrez que
« LMNP » est un parallélogramme . ( Pensez au théorème de la fiche 2 @ ) |
|
|
||
|
|
Activité 4 : |
|
|||
|
|
1°) Placez le point
« D » tel que « ABCD » soit un parallélogramme. Vous lisez : 2°) Calculons les
coordonnées de « D ». Soit (
x ; y ) les coordonnées
de « D ». « ABCD » est
parallélogramme signifie que |
|
|
||
|
|
C'est-à-dire |
|
|||
|
|
|
|
|||
|
|
3°) Déterminez de même les
coordonnées de « E » et « F » tels que « ABCD »
et AFBC » soient des
parallélogrammes. (Complétez la figure ) Faites les calculs sur
une feuille à part. Vous trouvez : E ( …. ; …..) ; F (
…. ; ….) |
|
|||
|
|
4°) Calculez les
coordonnées de Vous en déduisez que
« A ………………………………………………. » . Faites de même pour « B » et « C ». |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Fiche
suivante : les coordonnées du milieu d’un segment. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||