|
DOSSIER : En vous aidant du cours remplir ce document. |
Les diagrammes "à secteurs circulaires"
Et
construction d’un diagramme (à
secteurs) circulaire.
1°) Un diagramme circulaire
admet pour support un disque découpé en secteurs dont les aires sont …………………………………………………des différents constituants de la
population statistique .
2°) Dans un diagramme circulaire
( ou semi circulaire) , les mesures des angles des secteurs angulaires sont ………………………………………………….. aux effectifs (
ou aux fréquences) associé(e)s.
3°) Une fréquence de 100%
correspond à un angle de ……………………………….° pour un diagramme
circulaire et à ………………………………….
° pour un diagramme semi circulaire .
Evaluation : Partie 1
|
|
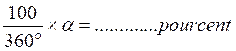
A) Le cercle est un arc de 360°. Ce secteur circulaire de 360° représente 100 % d’une population. 1 % ( un
pourcent ) représente
un secteur angulaire de B) 100 % de la population est
représentée par un angle de 360° . « avec « a » < 100 ; et
un angle
« α »
(inférieur à 360°) on peut calculer : Combien représente en % un angle
de valeur « alpha » soit la relation : |
|
|
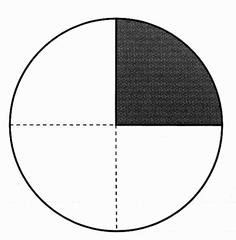
Quel est la valeur angulaire d’un quart de cercle ? Quel pourcentage représente – il ? |
|
|
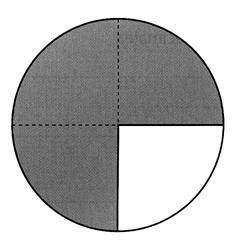
Quel est la valeur angulaire de trois quart de cercle ? Quel pourcentage représente – il ? |
|
|
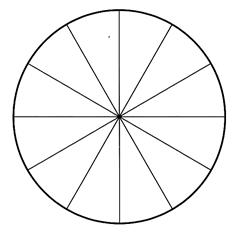
Questions : En combien de parties est divisé ce cercle ? Quelle est la valeur angulaire d’un secteur qui
représente les 8 / 12 du cercle ;et quel pourcentage représente – t-il ? |
Exemples d’applications du diagramme
à secteurs circulaire.
|
Soit la situation
suivante : |
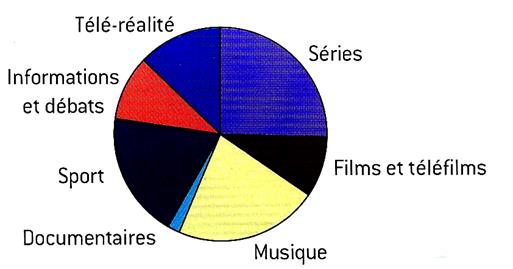
PB
1 : Quel pourcentage représente chaque secteur circulaire ? |
|
|
|
|
PB 2 : Retrouver les valeurs angulaires par le calcul et
vérifiez ?? |
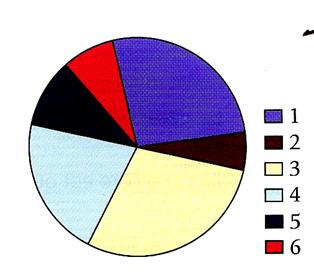
PB 3 / Quel pourcentage
représente chaque secteur circulaire ? |
|
|
|
|
|
|
Réponse :pb 3 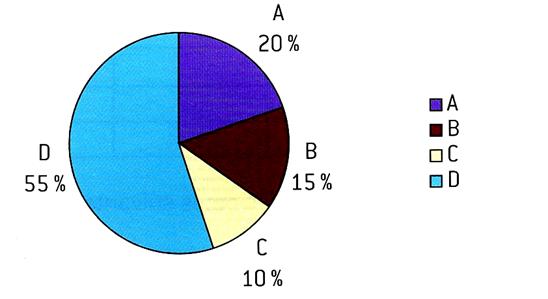
Interdisciplinarité :
|
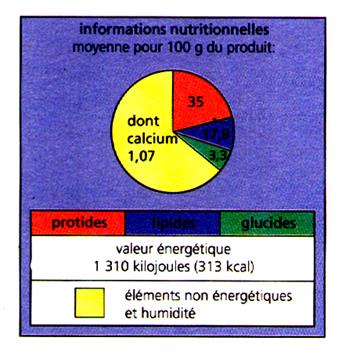
Les informations
suivantes sont tirées d’une étiquette
d’un fromage allégé |
|
|
Quelle analyse pouvez-vous en tirer ? |
|
|
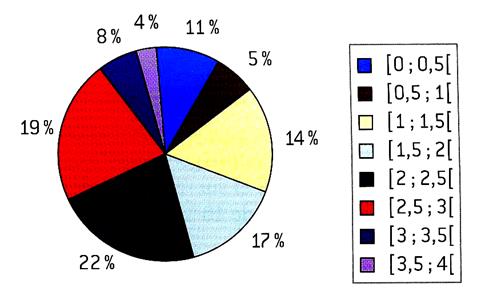
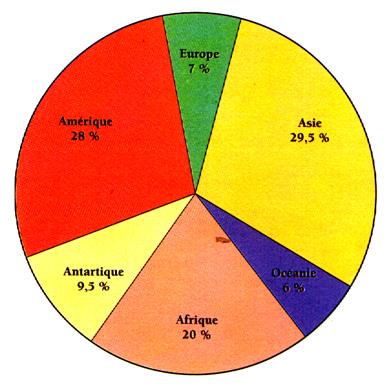
Liens en Secteurs angulaires et pourcentages: Soit le disque suivant (à vous de découvrir ce que
représente ces pourcentages) |
|
|
Activités : On demande de 1°) Vérifier que la somme des pourcentages est égale à 100%. 2°) Avec un rapporteur mesurer les secteurs angulaires
, vérifier que la somme de ces secteurs est égale à 360° |
|
Savoir
TRACER d'un diagramme à secteurs circulaires:
1°) Dans un diagramme
circulaire on partage un disque en secteurs
dont la mesure de l'angle au centre est proportionnelle à l'effectif de la valeur correspondante du caractère . ( n )
2°) Le diagramme à secteurs
circulaires est utilisé pour représenter graphiquement un caractère qualitatif ou quantitatif .
Remarque : la représentation graphique d'un caractère qualitatif
peut être aussi un diagramme en "bâtons".
|
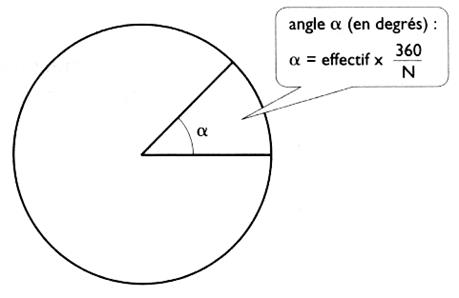
Les mesures des angles au centre des
secteurs sont proportionnelles aux effectifs correspondants. Un angle de 360° correspond à l'effectifs total : ……………………………………………………………………………………………………………………… A un effectif partiel "n" (donné) correspond un
valeur d’angle de : (voir l’équation) Recopier l’équation : Dire ce que représente les lettres : « α
« « n » « N »
Avec
quelle équation calcule-t-on la valeur
d’un angle a Complétez
l’égalité : a = …………………………………….. |
Activité 1 :
|
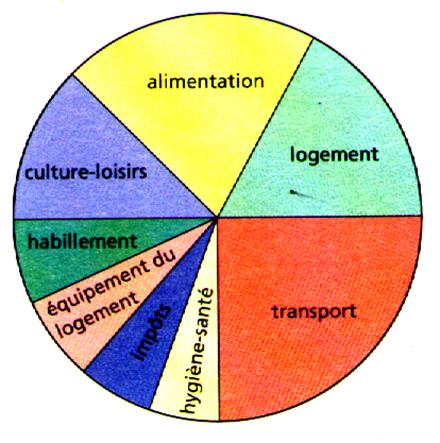
Ce diagramme représente les
dépenses d’une jeune personne salariée , en pourcentage . |
|||
|
Avec un rapporteur mesurer les secteurs
angulaires , |
|
||
|
Domaines
Logement Alimentation Culture
- loisirs Habillement Equipement
du logement Impôts Hygiène
- santé Transport Total
: |
Valeur
angulaire |
||
|
|
|
||
Activité 2 : on veut
construire un diagramme circulaire ;
|
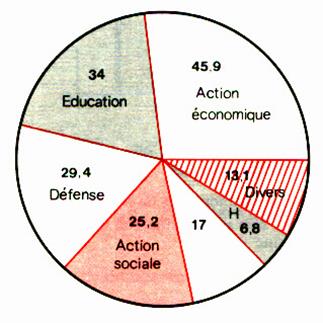
Exemple : Le budget de la France en 1969 correspond à 171,5 milliards de francs. Il est réparti ainsi : 45,9 pour l’
action économique 34 pour l’ éducation 29,4 pour la défense 25,2 pour l ‘ action
sociale 17 pour l’administration générale 6,8 pour l’ habitation 13,1 pour le « divers » On demande de déterminer par le calcul les valeurs angulaires (en degré) pour chaque partie composant le
budget de la France. . Calculs des valeurs angulaires : |
|
|
On applique la formule : 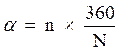
« n » désigne l’effectif ………………………………. ;
N désigne l’effectif ……………………….
Réponses.
"45,9" pour l’ action économique
sera représentée par un secteur angulaire d' angle : a =
"34" pour l’ éducation sera
représentée par un secteur angulaire d' angle : a =
"29,4" pour la défense sera représentée par un secteur
angulaire d' angle : a =
"25,2" pour l ‘
action sociale sera représentée par un secteur angulaire d'
angle : a
=
"17" pour l’administration générale sera représentée par un
secteur angulaire d' angle : a =
"6,8" pour l’ habitation sera
représentée par un secteur angulaire d' angle : a =
"13,1" pour le « divers » sera représentée par un
secteur angulaire d' angle : a =
Tracer le diagramme circulaire.
|
Activité 3 :
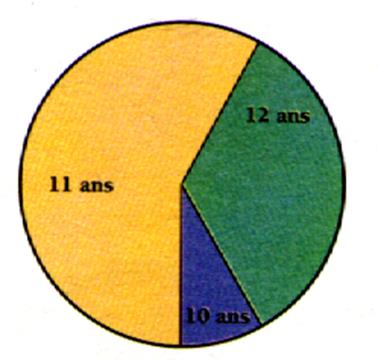
Traduire en pourcentage les catégories d’âges d’une classe de même
section. |
|
|
Solution : 1°) mesurer les secteurs
angulaires. A 10 ans correspond
……………………………… A 12 ans correspond
……………………………. A 11ans correspond
…………………………………………….. 2°) Exprimer en pourcentage la
représentation de ces catégories d’âges. Pour chaque catégorie d'âge appliquer la relation : -
10
ans : » -
-
11ans:
» -
-
12
ans : = -
|
|
Activité
4
|
Exemple : Le budget de la France en 1969 correspond à 171,5 milliards de francs. Il est réparti ainsi : 45,9 milliards pour l’ action économique 34 milliards pour l’ éducation 29,4 milliards pour la défense 25,2 milliards pour l ‘ action sociale 17 milliards pour
l’administration générale 6,8 milliards pour l’ habitation 13,1 milliards pour le
« divers » Question : exprimez en pourcentage ces répartitions. |
|
1°) Exprimer ces pourcentages en
valeur d’angles ; dont l’unité de mesure est le degré.
Niveau supérieur au bac professionnel.
2°) Exprimer ces pourcentages
en valeur d’angles ; dont l’unité de mesure est le grade
.
Il est possible de calculer l'angle d'un secteur angulaire ( en grade) d'une
composante en utilisant la relation:
a (grade) = ![]() ou "n"
est la valeur d'une composante et "N" la somme des valeurs des
composantes.
ou "n"
est la valeur d'une composante et "N" la somme des valeurs des
composantes.
Comme 100 % correspond au disque entier soit 400 grades , il en résulte que 1 % sera représenté par
4 grades . Sur le
diagramme circulaire ; on a tracé des secteurs angulaires dont les
angles au centre , ont pour valeur :
On utilisera la relation :
a (grade)= 4![]() a %
a % 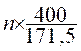
|
A « a% » |
26,8 |
19,8 |
17,2 |
14,7 |
9,9 |
4 |
7,6 |
|
Correspond l’angle en gr. |
107,2 |
79,2 |
68,8 |
58,8 |
39,6 |
16 |
30,4 |
Pour s’assurer que les calculs sont exactes il
faut vérifier que la somme correspond à
400 grades.