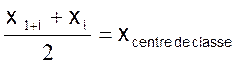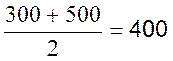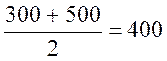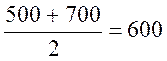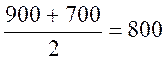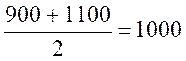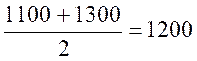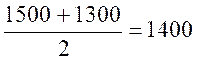|
Pré requis: |
|
||||||||||||
|
Lecture : Les
Statistiques info |
|||||||||||||
|
Les
intervalles |
|||||||||||||
|
ENVIRONNEMENT du dossier: |
|
||||||||||||
|
Objectif
précédent : |
Objectif
suivant : |
tableau |
Doc. 2 |
||||||||||
|
|
|
|
|
|
|||||||||
|
DOSSIER : « CLASSE » - Constitution d’une classe
, - « mode » et « classe
modale » (ici : info plus) - Calcul : « valeur centrale d’une
classe », - Calcul : « classes et
amplitude ». |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
TEST |
COURS |
Interdisciplinarité |
|
||||||||||
|
|
|
|
|
Observation des faits ( exemple de dépouillement ). |
||
|
Constitution
d’une classe , ENREGISTREMENT DES OBSERVATIONS et Exploitation et dépouillement
des données : Exploitation et dépouillement des données : : Supposons qu’on doive définir une statistique portant
sur les notes de cent élèves à la
suite d’un examen ;Les notes figurent dans le
tableau ci – dessous et ont été distribuées au fur et à mesure de la
correction. La liste de ces notes attribuées à chaque élève s’appelle
« série statistique » |
||
|
|
|
Ce tableau présente l’inconvénient
d’être volumineux .On peut choisir d’effectuer un regroupement des valeurs de
la variable (note) suivant 5 classes . Pour cela on partage l’intervalle [ 0 ;
20] en 5 intervalles partiels comprenant chacun 4 notes sauf le dernier qui
en contient cinq . On obtient les classes suivantes :
Ici : SOS écriture
normalisée |
|
|
|
|
[ 0 ; 4 [
groupant les xi tels que 0
£
xi < 4 [ 4 ; 8 [
groupant les xi tels que 4
£
xi <
8 [ 8 ; 12 [ groupant les xi tels que 8
£
xi <
12 [ 12 ; 16
[ groupant les xi tels que
12 £ xi
< 16 [ 16 ; 20
] groupant les xi tels que
16 £ xi
£ 20 .Les valeurs
2 ; 6 ; 10 ; 14 ; 18 , sont appelées « valeurs centrales » des classes . Dans ces conditions , le dépouillement se
présente suivant le nouveau tableau suivant : |
|
Classes des notes |
Nombres d’élèves |
|
[ 0 ; 4 [ [ 4 ; 8 [ [ 8 ; 12 [
(classe modale) [ 12 ; 16 [ [ 16 ; 20 [* *remarquez que le crochet exclu la valeur
20 |
3 19 42 26 10 |
|
|
|
|
CLASSE : |
|
|
|
|
« effectif » ; « effectif
total » |
|
Nous
avons vu ci-dessus que l'effectif
total des éléments pris en compte sont regroupés par catégorie ou
"classe". (les
classes (intervalles) sont imposées par le statisticien ) ; Les classes n'ont pas obligatoirement la même amplitude. L’
existence des valeurs entre les bornes
peuvent être différentes ; mais attention , lors de la représentation
graphique appelée "histogramme"
doit respecter l'aire de référence . Constitution d’une classe : Lorsque le caractère est
quantitatif (
mesurable ) ; on organise les
"réponses" en classe de nombres ,C'est à dire pour ce faire : |
|
On prend l'ensemble des réponses: exemple : les mesures des tailles des 30 individus
recensés dans le désordre sont rangées (classées) par groupe (classe) ;et on
les regroupe par "Classe" (les classes sont représentées par des
"intervalles" ,un intervalle est un segment de droite bornée en géométrie ) |
||||||||||||
|
Exemple les individus mesurant entre 158 et 162 constituent la classe 1 |
Exemple les individus mesurant entre 163 et 167 constituent la classe 2 |
Exemple les individus mesurant entre 168 et 172 constituent la classe 3 |
Exemple les individus mesurant entre 173 et 177 constituent la classe 4 |
Exemple les individus mesurant entre 178 et 182 constituent la classe 5 |
Exemple les individus mesurant entre 183 et 187 constituent la classe 6 |
Exemple les individus mesurant entre 188 et 192 constituent la classe 7 |
||||||
|
|
||||||||||||
|
|
||||||||||||
|
« Effectif » et « effectif
total » |
||||||||||||
|
Se souvenir · chaque classe possède son effectif… ( c’est le nombre d’individus qui entre dans la
classe) …… · Le « n i » est l’ effectif par classe. Dans un tableau on donne L' effectif par « classe » (qui est un "sous- effectif" ) ou un effectif
par « caractère » . Cet effectif
« par classe » ou « caractère » est noté par le petit
" n " avec un indice d'ordre : les
(n i ) · La
lettre « N » désigne la somme des« n i ». ·
ainsi l' effectif total est
la somme des éléments (n i )
qui sont inventoriés . Le symbole désignant l'effectif total est la lettre " N " |
||||||||||||
|
Reprenons l’exemple ci-dessus : nous avons 7 classes. (chaque classe possède son
effectif) |
||||||||||||
|
L'effectif de la
classe 2 est noté :n2 |
L'effectif de la
classe 3 est noté : n3 |
L'effectif de la
classe 4 est noté : n4 |
L'effectif de la
classe 5 est noté : n5 |
L'effectif de la
classe 6 est noté :n6 |
L'effectif de la
classe 7 est noté : n7 |
|||||||
|
Nous pouvons
calculer la somme des effectifs
en effectuant l’addition suivante : n1+ n2+ n3+
n4+ n5+ n6+ n7 D'où l' égalité :
N = n1+ n2+ n3+ n4+ n5+
n6+ n7 · D'où
la formule : N = On dira que l'effectif total est égal à la somme
des effectifs des classes données ( "i"
désigne le nombre de classes") |
||||||||||||
|
Chiffres d’ Affaire . ( en milliers
d’euros ) |
Effectifs :( n i ) |
22 + 25 +90+33+24+6 = 200 (classe
modale) |
300
à moins 500
|
22
|
|
500
à moins 800
|
25
|
|
800
à moins 1 000
|
90
|
|
1
000 à moins 1400
|
33
|
|
1
400 à moins 1500
|
24
|
|
1500
et +
|
6
|
|
(la somme des ( n i ) : N
|
200
|
N =![]() ainsi N
= 200
ainsi N
= 200
« MODE » et
« classe modale »
d’une série statistique :
Par définition : Un mode d’une série
statistique est une valeur du caractère correspondant au plus grand effectif ( ou à la plus grande fréquence.)
Notation : Mo
Vocabulaire
à connaître :
On dit « mode » d’une série
à variable discrète .
Et « classe modale»
d’une série à variable continue …
Généralement , les valeurs sont groupées en classe. La
classe correspondant au plus grand effectif est appelée « classe
modale ».
|
Chiffres d’ Affaire . ( en milliers
d’euros ) |
Effectifs :( n i ) |
L’effectif
« n 3 » de la classe « x 3 »
étant le plus grand . La classe
[800 ; 1000 [ est appelée la
« classe modale » ; 22 + 25 +90+33+24+6 = 200 |
300
à moins 500
|
22
|
|
500
à moins 800
|
25
|
|
800 à moins 1 000
|
n 3 = 90
|
|
1
000 à moins 1400
|
33
|
|
1
400 à moins 1500
|
24
|
|
1500
et +
|
6
|
|
(la somme des ( n i ) : N
|
200
|
Il
faudrait étudier les 2 cas : les classes ont la même amplitude et les
classes sont d’amplitude inégale.
Remarques :
► pour tracer le polygone des effectifs ou fréquences, il faudra rechercher pour
chaque classe observée : « son centre de classe » .appelé
aussi : « moyenne
de centre de classe » ou « valeur centrale d’une classe ».
► Dans le
calcul de l’écart type
, on prendra la valeur centrale de chaque classe comme « x
i » |
|||
« valeur centrale » d’une classe.
|
|||
exemple
|
|||
C.A. .(milliers
d’euros )
|
|
C.A. .(milliers
d’euros ) x i
Peut s’écrire |
Centre de
classe : x
i
|
300 à moins 500
|
|
[ 300 ; 500[
|
|
500 à moins 800
|
|
[ 500 ; 800[
|
( 500 + 800) /2
= 650
|
800 à moins 1 000
|
|
[ 800 ; 1000[
|
(800 +
1000) / 2 = 900
|
1 000 à moins 1400
|
|
[ 1000 ; 1400[
|
( 1000 + 1400 )
/2 = 1200
|
1 400 à moins 1500
|
|
[ 1400 ; 1500[
|
(1400 +
1500) / 2 = 1450
|
1500 et +
|
|
????
|
Il faudra
connaître le C.A. maxi
|
Dans le cas
d’un regroupement en classes , la valeur centrale
( noté : x i ) de la
variable statistique ewst égale à la demi somme des
valeurs extrêmes de chaque classe.
On se
souviendra que : dans les
calculs de l’écart type on admet
que les valeurs observées sont celles du « centre de la classe ».
|
|||
« Classe » et « amplitude »
|
||||
L’amplitude de classe est la distance entre les valeurs
extrêmes de la classe.
On
dit aussi : l’amplitude d’une
classe est la valeur de l’intervalle
compris entre les deux bornes de l’intervalle. La
représentation graphique des effectifs d’une variable continue ( organisation de « classe » pour ranger ces
effectifs) peut s’effectuer sous la
forme d’un histogramme.
·
Pour respecter le principe de construction de
l’histogramme, on devra veiller à vérifier que les intervalles de toutes les classes sont égaux.
, On dit que les classes
doivent avoir la même amplitude. |
||||
Exemples :le tableau
1 n’est pas exploitable ; le tableau
2 est exploitable.
|
||||
Tableau 1
|
|
Les
classes sont d’amplitudes inégales
|
||
[ 300 ; 500[
|
.
|
500 – 300 = 200
|
Cette série
ne sera pas exploitable pour tracer un histogramme. Il faudra repenser la
distribution. Voir
« l’informaticien »
|
|
[ 500 ; 800[
|
800 – 500 = 300
|
|||
[ 800 ; 1000[
|
1 000 – 800 = 200
|
|||
[ 1000 ; 1400[
|
1400 – 1000 = 400
|
|||
[ 1400 ; 1500[
|
1500 – 1400 = 100
|
|||
|
|
|
|||
Tableau
2 :
|
|
Les classes sont d’égales amplitudes
|
||
[ 300 ; 500[
|
.
|
500 – 300 = 200
|
L’amplitude
est de 200 .
Cette série
est exploitable pour tracer un histogramme.
|
|
[ 500 ; 700[
|
700 – 500 = 200
|
|||
[ 700 ; 900[
|
900 – 700 = 200
|
|||
[ 900 ; 1100[
|
1100 – 900 = 200
|
|||
[ 1100 ; 1300[
|
1300-1100= 200
|
|||
[ 1300 ; 1500[
|
1500 – 1300 = 200
|
|||
|
|
||||
La
valeur centrale d’une classe :
Dans le cas d’un regroupement en classes , la valeur centrale ( notée : xi ) de la variable statistique est
égale à la demi- somme des valeurs extrêmes de chaque classe ;
Tableau
2 :
|
|
Valeurs centrales ( notée : xi )
|
||
[ 300 ; 500[
|
.
|
|
|
|
[ 500 ; 700[
|
|
|||
[ 700 ; 900[
|
|
|||
[ 900 ; 1100[
|
|
|||
[ 1100 ; 1300[
|
|
|||
[ 1300 ; 1500[
|
|
|||
|
|
||||
Cas général d’une classe [ ai ; b i
[
1°)
L’amplitude
de la classe de rang « i »
est égale à :
b i - ai
2°)
La valeur centrale
xi de la classe de
rang i
est égale à 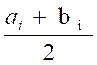
|
|
|
|
|
Exemple de résolution de PROBLEME : |
|
|
Nous relevons les tailles
en cm de 30 individus adultes , pris au hasard. A
chaque individu correspondra une
taille. Nous disposons d'une distribution de la taille en fonction
des individus. Nous dirons que la taille
varie en fonction des individus. La taille
, cette caractéristique de chaque individu est la variable ,( caractère ) et l'
événement est le couple « taille individu » . Après « recensement _ sondage » (barrer un des mots ) des
variables ( appelées
aussi : ……caractère ……) , nous obtenons le tableau de données
suivant: On nous donne le tableau suivant à remplir : |
|
|
Tailles
en cm |
158 |
159 |
160 |
161 |
162 |
163 |
164 |
165 |
166 |
167 |
168 |
|
nombre |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
2 |
0 |
0 |
0 |
|
Tailles
en cm |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 |
178 |
179 |
|
nombre |
1 |
0 |
2 |
2 |
3 |
0 |
3 |
1 |
2 |
2 |
2 |
|
Tailles
en cm |
180 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
188 |
189 |
190 |
|
nombre |
1 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
Nous constatons que certains
événement se produisent 3 fois , deux fois , d'autres
une fois et d'autres pas du tout.
A partir de ces donnée nous décidons de
regrouper ces tailles par classe .
On décide de regrouper la taille des individus « en classe » de
Dans
1ère classe on
regroupe les tailles comprise entre 158 et
Ensuite, nous « distribuons »
les effectifs .
Nous
obtenons le tableau intermédiaire
ci-dessous :
|
Valeurs
extrêmes |
158-162 |
163-167 |
168-172 |
173-177 |
178-182 |
183-187 |
188-190 |
|
Calcul,
des Valeurs centrales |
(158 +
162) : 2 |
(163 + 167 ) : 2 |
(168 +
172) : 2 |
(173 + 177 ) : 2 |
(178 +
182) : 2 |
(183 + 187
) : 2 |
(188 +
190) : 2 |
|
effectifs |
1 + 1 |
1+1+2 |
1 + 2 + 2 |
3 + 3 + 1 +2 |
2 + 2 + 1 + 1 |
2+1 |
1 |
Soit le
tableau final :
|
Classe
|
[158-162[
|
[
163-167 [ |
[
168-172 [ |
[173-177
[ |
[
178-182 [ |
[
183-187[ |
[
188-190[ |
|
Valeurs
centrales |
160 |
165 |
170 |
175 |
180 |
185 |
190 |
|
effectifs |
2 |
4 |
5 |
9 |
6 |
3 |
1 |
Questions :
1°) Quelle est la valeur d’une classe . ? 5 cm
2°) Comment a-t-on calculer les valeurs
centrales ? somme des valeurs extrêmes
divisée par 2
3°) Q’appelle t- on
« effectif » ? le nombre de tailles
par classe.
4°) Combien y a – t- il de classes ? 7 classes