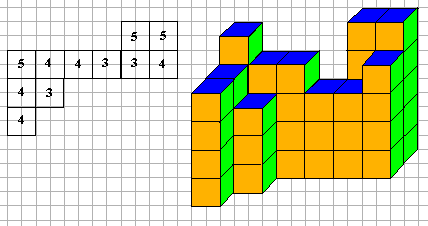|
WARMATHS |
Perspective
|
- Introduction.
- Définitions.
- Exemple 1: le carré.
- Exemple 2: le cube.
- Exemple 3: le cercle.
- Exemple 4: pas de faces frontales.
- Utilisation d'un quadrillage.
- Jeu de construction.
La perspective exposée dans ce document est appelée perspective cavalière ou fuyante. Nous n'en donnerons pas de formulation purement mathématique, mais seulement un minimum de théorie et quelques "recettes" pour dessiner d'une façon assez réaliste des objets simples de l'espace à trois dimensions.
Pour dessiner un solide à l'aide de la perspective cavalière il faut distinguer:
-le point de vue:
C'est l'endroit où se trouve l'observateur. Pour que l'objet soit représenté avec un certain effet de volume il faut que l'observateur soit placé un peu à droite ou à gauche sur une droite horizontale (parallèle à la droite d'horizon) et un peu au dessus ou au dessous sur une droite verticale (perpendiculaire à la droite d'horizon). Ce qui donne quatre types de points de vue.
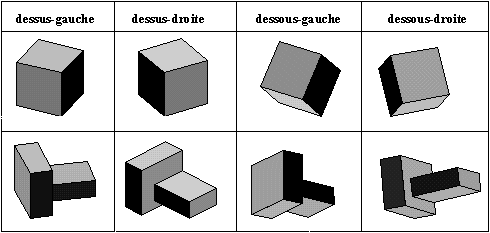
Le point de vue est choisi par le dessinateur en fonction de l'effet qu'il veut produire. Ce point de vue n'est pas noté sur le dessin. Nous indiquons parfois son type: dessous à droite, dessous à gauche, dessus à droite et dessus à gauche.
-les faces frontales:
Ce sont les faces situées dans un plan perpendiculaire à notre regard. Leurs dimensions (longueurs, largeurs, hauteurs, rayons,...) sont conservées. Les angles ont leur mesure réelle. Ces faces sont dessinées dans leurs formes réelles, à l'échelle.
-les faces fuyantes:
Ce sont les faces qui forment les côtés. Les segments verticaux sont représentés par des segments verticaux dont les longueurs sont les vraies longueurs.
Les mesures des angles ne sont pas conservées (par exemple: des droites perpendiculaires dans la réalité ne le sont plus sur le dessin).
Le parallélisme est conservé: des faces qui contiennent des droites parallèles, sont dessinées avec des droites parallèles.
Le partage en segment égaux, sur les segments fuyants, est conservé et notamment le milieu.
Toutes les droites verticales sont représentées par des droites verticales. Les dimensions sur ces droites verticales sont en vraie grandeur.
Toutes les droites horizontales de l'objet sont représentées par des droites fuyantes parallèles. Les dimensions sur ces droites fuyantes sont diminuées.
Pour respecter ces règles nous utilisons un angle de fuite et un coefficient de fuite.
Angle de fuite: c'est l'angle que font toutes les droites fuyantes d'une face fuyante, avec l'horizon du dessinateur.
Coefficient de fuite: c'est le nombre par lequel nous multiplions les dimensions réelles des segments fuyants (sur les droites fuyantes) pour obtenir leurs dimensions sur le dessin.
|
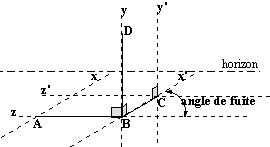
Sur la figure ci- contre: -(Bz) et (Cz') sont des droites horizontales et frontales. Elles sont parallèles. -(Ax) et (Bx') sont des droites fuyantes. Elles sont parallèles. -(By) et (Cy') sont des droites verticales et frontales. Elles sont parallèles. Elles sont aussi perpendiculaires aux droites horizontales et frontales. -La distance BC est obtenue en multipliant la dimension réelle de l'objet par le coefficient de fuite.
|
|
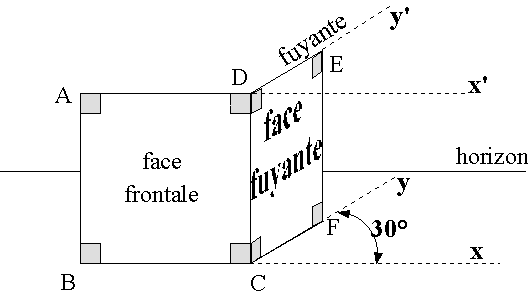
Exemple 1: dessin d'un carré de 3cm de côtés en face frontale et en face fuyante.
L'angle de fuite est 30°. Le coefficient de fuite est 0,5. Point de vue: dessus-droite.
Carré frontal: il est dessiné comme d'habitude (ici il est vu en vraie grandeur).
Carré sur face fuyante: les côtés[DC] et [EF] sont verticaux et leur dimension (3cm) sont conservées sur le dessin. Les fuyantes sont (CF) et (DE) et font un angle de 30° avec l'horizon (les angles xCy et x'Dy' sont égaux à 30°). Elles sont parallèles dans le carré CDEF et le restent sur le dessin. Mais la longueur des côtés fuyants [CF] et [DE] a été multipliée par 0,5, le coefficient de fuite (vous portez donc CF=DE=3*0,5=1,5 sur deux droites parallèles (Cy) et (Dy') ).
Remarques:
-Les petits carrés (en gris sur la figure) qui indiquent que nous avons des angles droits sont de vrais carrés sur la face frontale mais représentés par des parallélogrammes sur la face fuyante (les longueurs des côtés fuyants de ces parallélogrammes sont égales à la longueur d'un côté d'un petit carré, multiplié par 0,5).
-Les diagonales sur la faces frontales représenteraient correctement, si elles étaient dessinées, les propriété des diagonales d'un carré
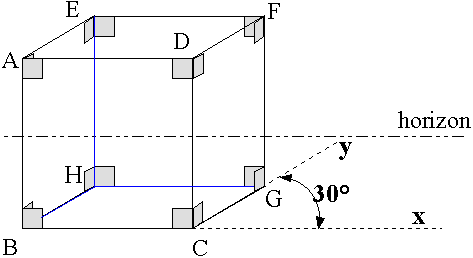
Exemple 2: dessin d'un cube de 3cm d'arête.
L'angle de fuite est 30°. Le coefficient de fuite est 0,5. point de vue: dessus-droite.
L'exemple 1 donne la marche à suivre pour commencer le dessin de ce cube. Nous appellerons notre cube ABCDEHGF.
Nous avons deux faces frontales (une devant et une derrière), quatre faces fuyantes (une dessous, une dessus et une de chaque côtés à droite et à gauche).
Nous dessinons en bleu (en pointillés si vous préférez) les arêtes cachées.
Remarques:
-Nous avons indiqué l'horizon et tous les angles droits des faces latérales. Ce qui, dans une figure courante, n'est pas conseillé (afin de ne pas l'encombrer vous n'indiquerez que les éléments nécessaires à votre recherche pour une démonstration). De même pour l'indication de l'angle de fuite (pratiquement c'est vous qui le choisirez, alors il est inutile de le représenter).
-Les côtés fuyants sont tous de même longueur (égale sur le dessin à 3cm multipliés par 0,5, soit 1,5cm) et parallèles. Les deux faces frontales (ABCD et EFGH) sont en vraie grandeur ainsi que les segments verticaux.
Exemple 3: dessin d'un cercle de 3cm de diamètre.
|
Dessiner sur trois faces d'un cube (une frontale, une latérale et une de dessus) un cercle de 3cm de diamètre avec comme angle de fuite 30° , comme coefficient de fuite 0,5 (ce qui revient à diviser par 2) et comme point de vue: dessus-droite. Les faces d'un cube étant des carrés, nous allons utiliser le cercle inscrit dans un carré de 3cm de côté. |
|
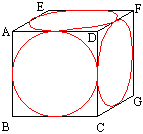
Nous allons commencer par le plus facile: tracer le cube ABCDEHGF et le cercle inscrit dans le carré de la face frontale ABCD. Son centre est à l'intersection des diagonales ( en vert) et des médianes (en bleu) du carré ABCD. Nous traçons aussi les diagonales et les médianes des autres faces (les milieux restent des milieux sur les fuyantes).
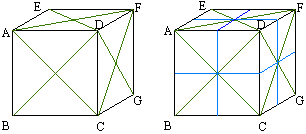
Dès que le cercle inscrit dans ABCD est tracé nous obtenons huit points caractéristiques: intersections de ce cercle et des médianes et des diagonales. Sur les autres faces, qui sont aussi des carrés, les cercles inscrits dans ADFE et CDFG passent par des points identiques. Pour les obtenir nous traçons (en pointillés) des lignes de report (parallèles aux côtés des carrés et passant par ces points 2 par 2).
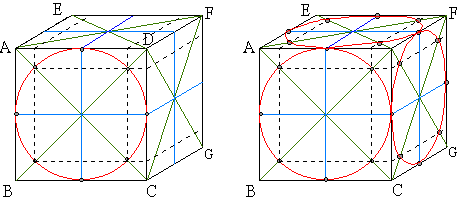
Il ne reste plus qu'à joindre ces points, sur chaque face, par un trait continu tout en rondeurs... ce qui n'est pas forcément le plus facile! Vous venez de dessiner deux cercles sur des faces fuyantes.
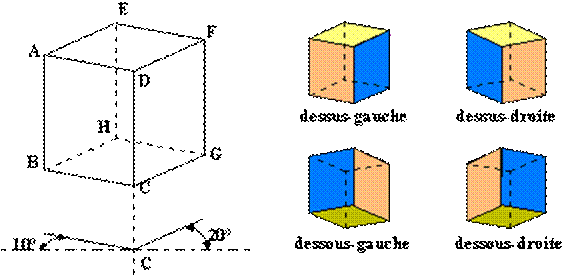
Exemple 4: dessins d'un cube de 3cm d'arête dont aucune des faces n'est frontale.
Nous appellerons notre cube ABCDEHGF comme ci-dessus.
1. Dans un premier temps nous allons garder quatre arêtes verticales (elles mesurent donc 3cm):[AB], [DC], [FG] et [EH]. Les faces latérales visibles seront ABCD et CDFG. Aucune des deux ne sera frontale: il faut donc deux coefficients de fuite ainsi que deux angles de fuites.
|
Nous prendrons donc comme paramètres: -pour ABCD: 0,8 et 10°. -pour CDFG: 2/3 (ou 0,66) et 20°.
Points de vue: Avec le même dessin de base (après échange des paramètres de perspective de ABCD et CDFG) nous pouvons donner différentes interprétations de ce que nous voyons en utilisant les pointillés pour les arêtes cachées, ou le coloriage des faces (solution "encombrante" pour une figure qui doit aider à la recherche d'une solution mais tout à fait indiquée pour suggérer les volumes). Nous avons utilisé ici les deux. |
|
|
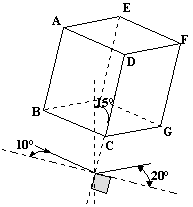
2. dans un second temps, nous gardons les mêmes arêtes frontales mais "penchées" de 15° (il ne s'agit pas ici d'un angle de fuite puisque ces arêtes sont frontales). c'est une difficulté de plus à gérer. Avec les mêmes données que ci-dessus, nous obtenons la figure ci-contre.
|
|
|
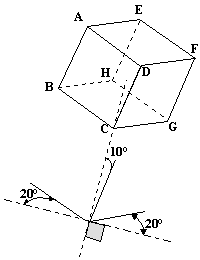
3. Et si il n'y avait plus aucune arête frontale? Il nous faut un troisième angle de fuite (par exemple 10°) et un nouveau coefficient de fuite (par exemple 0,8). Nous appliquerons ces paramètres à l'arête [CD] et, bien sûr, aux arêtes qui lui sont parallèles. Pour [BC] nous modifions l'angle de fuite: 20° au lieu de 10° (nous trouvons que c'est plus réaliste avec cette donnée...).
|
|
Nous allons exploiter le fait que vous travaillez le plus souvent sur des feuilles quadrillées (carrés de 8x8mm ou 5x5mm). Dessiner rapidement un cube sur de tels support est très facile et rapide. Munissez vous d'une feuille quadrillée 5x5mm et suivez nous.
Il suffit de savoir compter les carreaux: d'abord horizontalement puis verticalement. Par exemple avec le petit cube ci-dessous: pour aller
du point 1 au point 2: 2 carreaux horizontalement puis 0 carreau verticalement.
du point 2 au point 3: 1 carreau horizontalement puis 1 carreau verticalement.
Ce qui peut s'écrire plus vite: de 1 à 2: (2;0), et de 2 à 3: (1;1)
Pour le cube du milieu ci-dessous: de 1 à 2: (3;0) et de 2 à 3: (2;1).
Pour un cube:
|
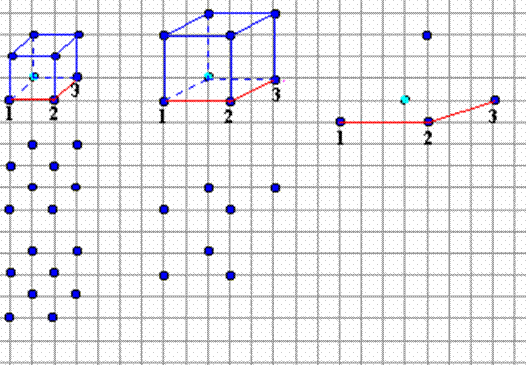
Ex1: cube de 1cm d'arête; l'angle de fuite est 45° et le coefficient de fuite est environ 0,7 Ex2: cube de 1,5cm d'arête; l'angle de fuite est environ 26,5° et le coefficient de fuite 0,75 environ. Ex3: cube de 2cm d'arête; l'angle de fuite est environ 18° et le coefficient de fuite est environ 0,8. Terminez les figures inachevées ci-contre en changeant de point de vue. Sur vos figures il n'est pas nécessaire de mettre des points aussi gros!.. |
|
Pour une pyramide:
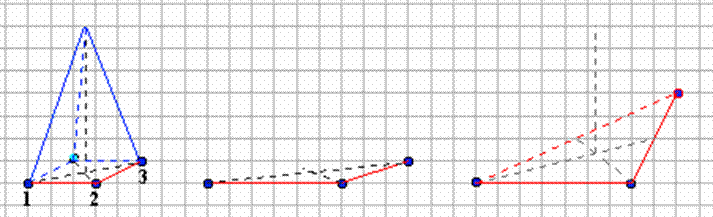
Exemple de pyramide régulière à base carrée (première figure ci-dessous).
Terminez le dessin d'une autre pyramide régulière à base carrée avec d'autres données (deuxième figure ci-dessous) et celui d'une pyramide régulière à base triangulaire (le triangle est donc équilatéral) sur la dernière figure ci-dessous.
Pour un cylindre droit:
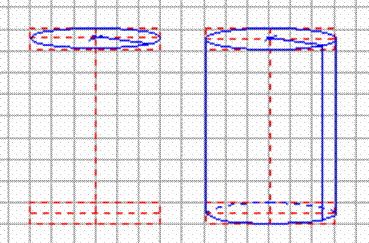
Comme un cylindre n'a qu'une face latérale, nous allons nous simplifier la tache en dessinant une vue de face par dessus. Chaque base du cylindre est dessinée dans un carré vue de face par dessus. ce carré est donc représenté par un ... rectangle.
|
Si nous prenons un diamètre de 3cm (soit 6 petits carreaux) et une hauteur de 4cm, un diamètre frontal est représenté par un segment de 3cm et une génératrice du cylindre (segment frontal) par un segment de 4cm.
|
|
Pour un cône droit:
|
La base du cône est dessinée comme celles du cylindre droit. Les génératrices (segment joignant le sommet à un point du cercle de base) sont représentées par des segments de longueur variable (ainsi que les rayons du disque de base). |
|
Pour une sphère: (n'est pas au programme de 4ème...)
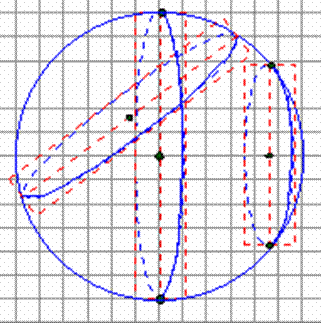
Les cercles horizontaux et verticaux sont, comme pour le cylindre et le cône, dessinés dans des rectangles dont l'une des dimensions diminue lorsque le plan du cercle s'éloigne du centre de la sphère (sinon le cercle serait dessiné en dehors de la sphère..).
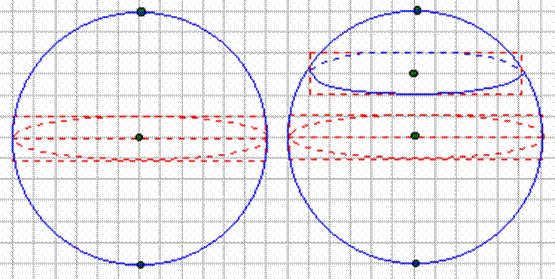
Quant aux cercles dans des plans obliques (ni horizontaux, ni verticaux) ils sont contenus dans des rectangles de même nature que ceux utilisés ci-dessus. Ces rectangles sont dessinés obliquement. La figure ci-dessous en représente un, ainsi que deux cercles dans des plans verticaux.
Jeu de construction:
Une construction est constituée de "modules" cubiques. Sur le plan, les nombres indiquent le nombre d'étages (nombre de modules superposés).
Donner une représentation en perspective de cette construction avec pour point de vue "dessus-droite".
En voici la solution... à terminer.
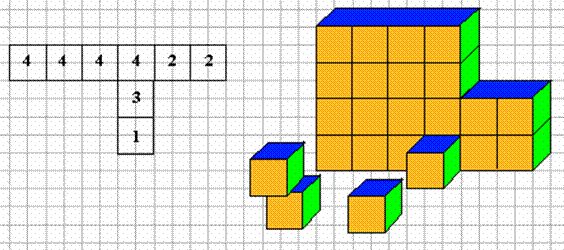
Voici un autre exemple de ce type d'exercice (complètement fini celui là!)