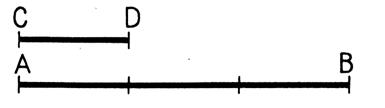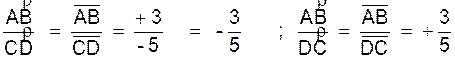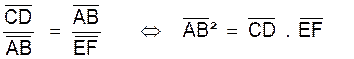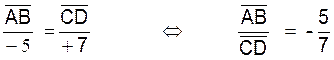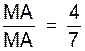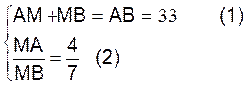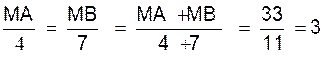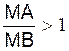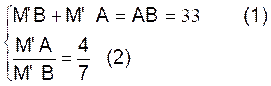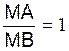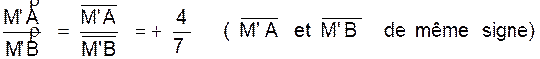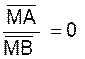|
|
||||||||||||
|
|
||||||||||||
|
ENVIRONNEMENT du
dossier: |
||||||||||||
|
Objectif précédent : |
Objectif suivant : |
►tableau |
||||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
INFO :Géométrie
plane : RAPPORT DE DEUX
SEGMENTS |
||||||||||||
|
TEST |
COURS |
|
||||||||||
|
|
||||||||||||
COURS
|
||||||||||||
Définition :
la définition générale du rapport de deux grandeurs s’applique au cas de
deux segments de droite.
|
||||||||||||
On appelle rapport de deux segments
de droite le nombre par lequel il faut multiplier le second pour obtenir le
premier.
|
||||||||||||
Exemple 1:
|
||||||||||||
|
AB
est la somme de 3 segments égaux à CD On
a AB = 3 fois CD ou AB = 3 CD Donc :
|
|
|||||||||||
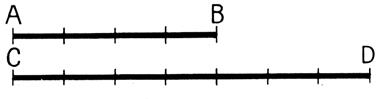
Exemple 2 :
|
||||||||||||
AB est égal à la somme de 4
segments égaux au septième de
CD :
On
a AB =
CD fois ( 4/7)
|
|
|||||||||||
Nous supposerons
, dans ce cours, que le rapport de deux segments est un nombre entier
ou fractionnaire. Cependant , il n’en est pas
toujours ainsi. On peut en effet supposer qu’aucun multiple de CD , si petit soit -il , ne soit contenu exactement dans AB .
|
||||||||||||
|
|
||||||||||||
2°) Propriétés du rapport de deux segments :
|
||||||||||||
Les propriétés des rapports de deux grandeurs deviennent
ici
a)
le rapport de deux segments est la mesure
du premier quand on prend le second pour unité. Dans
l’exemple 1 le nombre 3est la mesure
de AB , l’unité étant CD. Dans
l’exemple 2 : (4/7)
est la mesure de AB dont l’unité est CD. b)
Le rapport de deux segments est égal au
rapport des nombres qui les mesurent , avec la même
unité. Ainsi , dans le symbole (
AB / CD) nous supposerons que AB et CD sont les nombres qui mesurent AB et CD avec la même unité. La détermination du rapport de deux
segments se trouve ramenée au calcul du quotient exact de leurs longueurs. |
||||||||||||
3°) Vecteurs portés par un axe. ( @ vecteur)
|
||||||||||||
La mesure algébrique de AB
noté
|
||||||||||||
Ainsi : (voir ci dessous)
|
||||||||||||
|
|
||||||||||||
Notons que :
|
||||||||||||
Le rapport de deux vecteurs portés
par un même axe est égal au quotient exa t de leurs mesures algébriques sur cet axe.
|
||||||||||||
b) La mesure algébrique
|
||||||||||||
b)
Les mesures
|
||||||||||||
POINTS DIVISANT UN SEGMENT DANS UN RAPPORT DONNE.
|
||||||||||||
Problème : soit un segment
AB = 33 cm portée par la droite xy (figure ci dessous)
|
||||||||||||
|
|
||||||||||||
Trouver les points « M »
de cette droite tels qu’ on ait :
|
||||||||||||
Théorème :
1°)
le résultat précédent est général : Il
existe deux points divisant un segment AB dans un rapport arithmétique donné
« k » différent de l’unité. En effet si
2°)
Si la droite « xy » est orientée , on a ( figure ci dessous) |
||||||||||||
|
|
||||||||||||
|
Il
existe donc un point et un seul
divisant un segment AB dans un rapport algébrique donné « k »
différent de « 1 ». Si
le rapport donné est positif , le point est
extérieur à AB . Si le rapport donné est
négatif , ce point est entre A et B . Si le
rapport donné est nul , on a
Voir
les exercices. |
||||||||||||
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
Travaux : CONTROLE: Etudier le cours. 1°) soit
un segment AB= 18 cm a)
trouver les points M et M’ qui divisent AB dans le
rapport 5/7 b)
calculer le rapport
( AM / AB ) sans calculer MA , et le rapport
( M’A / AB) sans calculer M’A. c)
Calculer MM’. 1°) soit
un segment AB= 57cm a)
trouver les points M et M’ qui divisent AB dans le rapport 11/ 8 b)
Calculer MM’. EVALUATION: Donner des exemples : |