Pré requis:
|
Info : liste
des connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
AVANT :
|
APRES :
|
Complément d’Info :
1°) Liste des cours : prépa concours
A consulter pour
compléments : |
||
|
|
|
|
|
|
TITRE :PREPARATION CONCOURS niveau IV :
APPLICATION DES
FONCTIONS PRIMITIVE à l’élévation
des grandeurs.(moment d’inertie )
En cours
|
|
|
|
|
|
Applications : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Contrôle |
évaluation |
|||
COURS
|
|
|
|
||
|
|
Méthode générale . |
|
||
|
|
La méthode générale consiste à assimiler la
grandeur à évaluer à une fonction d’une variable et à chercher directement ( par des considérations géométriques par exemple), la
dérivée de cette fonction. On est ainsi ramené à trouver une fonction
admettant une dérivée connue. Le calcul fait intervenir une constante
arbitraire, dite « constante
d’intégration » , que l’on détermine dans un
cas particulier. |
|
||
|
|
Ci-dessous : nous voyons des exemples
d’application qui vont vous donner une
idée de la marche à suivre dans la plupart des cas. |
|
||
|
|
|
|
||
|
|
Aire d’un segment de courbe. |
|
||
|
|
Nous savons que les lignes usuelles ( droite ; cercle ; conique ;…) peuvent
être représentées par des équations. Il en est de même pour beaucoup de lignes courbes . L’équation de la courbe est la relation qui
existe entre les coordonnées
« x » et « y » d’un quelconque de ses points. |
|
||
|
|
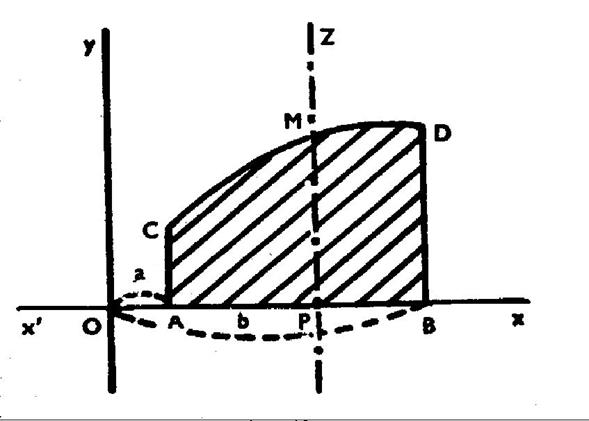
En particulier
( figure ci contre)
si la courbe n’est rencontrée qu’en un seul point « M » par toute
parallèle « PZ » à l’axe
« O y », son équation est du premier degré en « y »,
puisqu’à toute valeur « OP » de « x » ne correspond
qu’une valeur « PM » de « y ». On peut donc mettre cette
équation sous la forme : «
y = f ( x ) » Nous nous proposons d’évaluer l’aire de « ABCD » comprise entre la courbe , l’axe « O x » et les ordonnées
« AC » et « BD » correspondant aux abscisses « Soit « F ( x
) » une primitive quelconque de la fonction « f
( x ) » On sait que l’aire « ACMP » limitée à l’ordonnée du point
« M » d’abscisse « « ACMP =
F ( x ) + C ». Pour déterminer la constante « C »,
donnons à la variable « x » la valeur particulière « a ».
L’ordonnée Cette relation donne la valeur de
la constante « C » ; d’où « ABCD = F ( x ) - F
( a ) » Si l’on veut maintenant l’aire du segment
« ACDB » , il faut faire coïncider |
|
|
|
|
|
|
|
||
|
|
Exemple 1 : Aire du segment de la parabole. |
|
||
|
|
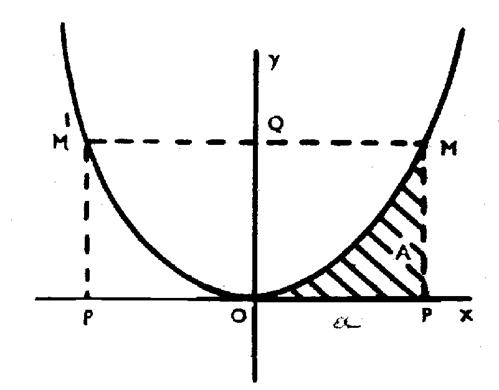
L’équation d’une parabole de paramètre
« p » rapportée à sa tangente au sommet « O x »et à son
axe de symétrie « O y » , est :
« x² = 2 p y » Cherchons l’aire « A3 du segment
« OPM » limité par la parallèle à « O y »menée par le
point « P » d’abscisse « OP = a ». Nous avons ici : «
y = f ( x
) = qui a pour
primitive : «
F ( x ) = L’aire de « A » est la différence des
valeurs que prend F(x) quand on y remplace « x » par les abscisses
des points « P » et « O » . par
suite : « A = F ( a
) - F ( 0 ) = ou bien : « A =
L’aire « OMP » est donc le tiers du rectangle
« OPMQ » et qu’on en conclut que l’aire du segment parabolique « MOM’Q »
égale les deux tiers de l’aire du rectangle « MPP’M’ » |
|
|
|
|
|
Exemple 2 : Aire d’une sinusoïde .
|
|
||
|
|
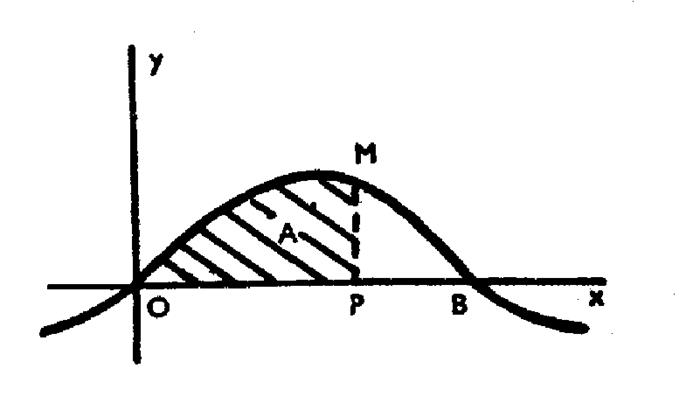
Soit la courbe
sinusoïdale (ci contre) représenté par l’
équation : « y = sin x » Cette aire est une fonction de
« x » dont nous ne connaissons pas la forme .
Mais il nous est possible du moins de calculer sa dérivée, qui est la limite
du rapport : (voir
cours niveau 3) Pour une
courbe quelconque ayant une équation : « y = f ( x ) » ; on a trouvé : « lim
Nous aurons donc ici : « L’aire de « A » est donc la primitive
de « sin x » ; donc : « A = - cos x + C » La constante se détermine en remarquant que , l’aire de « A » s’annulant pour « x =
0 » , on doit avoir : « 0 = -1 + C » d’où
« C = 1 » Par suite , l’aire
« OMP » est donné par la formule : « A = 1 – cos x » En particulier , l’aire
« OMB » s’obtient en faisant « x = |
|
|
|
|
|
|
|
||
|
|
VOLUME d’un solide . |
|
||
|
|
Soit ,
par exemple, à calculer le volume d’un segment sphérique dont l’une des bases est un grand
cercle . ( voir ci contre)
Le volume « V » du segment dépend de sa hauteur que nous
désignerons provisoirement « x » ; cherchons sa dérivée . Donnons a « x » l’accroissement « « V » est évidemment compris entre les
volumes des deux cylindres de même
hauteur « En désignant par « S » et
« S’ » les aires de ces cercles , on
a : « S’ . D’où : «
S’ < |
|
|
|
|
|
Or , quand « «
lim. |
|
||
|
|
« |
|
||
|
|
L’aire « S » est fonction de
« x » facile à évaluer. On a , en effet,
« R » étant le rayon de la sphère. : «
S = d’où « |
|
||
|
|
Le volume « V » est une fonction
primitive de « |
|
||
|
|
|
|
||
|
|
Cette constante est nulle ,
puisque l’on doit avoir : «
V = 0 » pour « x =
0 » |
|
||
|
|
|
|
||
|
|
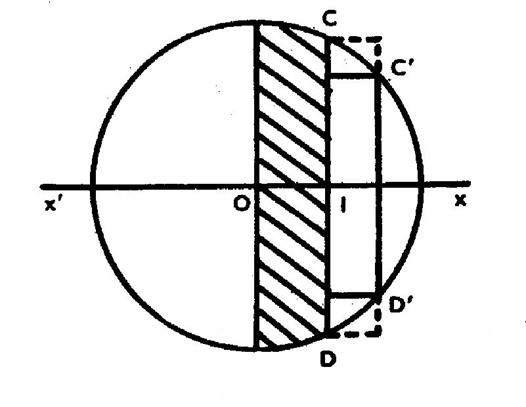
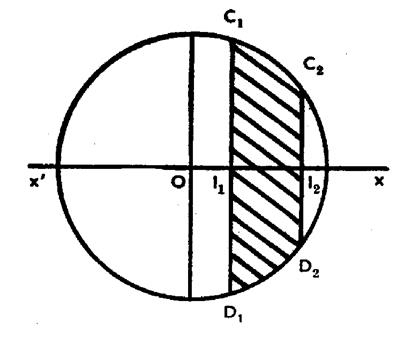
De la formule précédente ,
on déduit facilement le volume d’un segment sphérique à bases parallèles
quelconque, un tel segment étant
la différence ( ou la
somme) de deux segments limités à un
grand cercle. On a ainsi : (voir figure ci contre) « Vol. ( C1
D1 C 2 D2 ) = = |
|
|
|
|
|
Appelons « r » et « r2 »
les rayons des cercles de base du segment, « h » sa hauteur et
remarquons que : « x2
–x1 =
h » ; R² - x12 = r12 ;
R² - x22
= r22 » L’identité : « ( x2
– x1 )² = x12 + x22
– 2 x1 x2 » Donne : « h² = 2 R² - (r12 + r22 )
– 2 x1 x2 » D’où
x1 x2
= R²- |
|
||
|
|
On peut
transformer l’expression du volume : V
= |
|
||
|
|
V
= |
|
||
|
|
Ou
finalement : On
retrouve ainsi la formule de
géométrie élémentaire. |
|
||
|
|
|
|
||
|
|
Moment d’inertie d’une surface. |
|
||
|
|
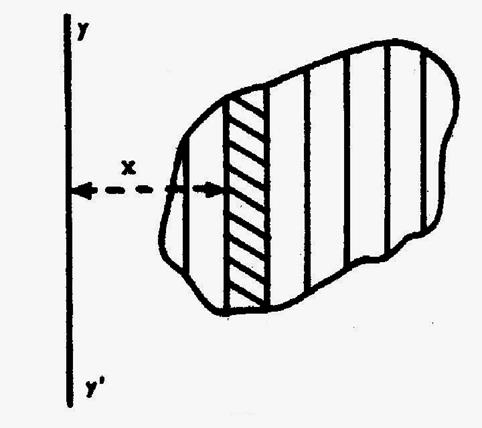
On défini le moment
d’inertie d’une surface « S » par rapport à un axe
« y’y »dans le cours de « Mécanique ». On décompose la surface en bandes très étroites
par des parallèles à « y’y », multiplions l’aire « S1 »…de
chaque bande par le carré de sa
distance : x1 ;
x2 ; x3 ;….à l’axe « y’y ». La limite de la somme « S1 x12 + S2
x22 +…..quand la largeur de bandes tend vers zéro, est
le moment d’inertie de la surface par rapport à l’axe « y’y » |
|
|
|
|
|
Exercice 1 |
|
||
|
|
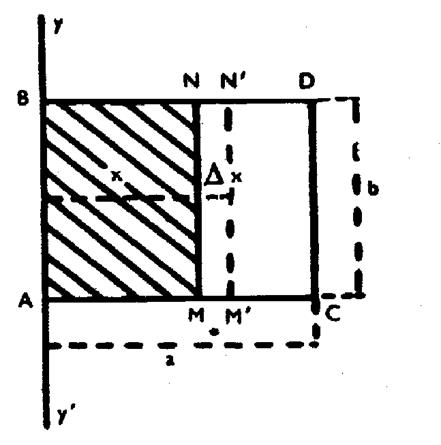
: Chercher
le moment d’inertie d’un rectangle par rapport à l’un des côtés
« AB » (
voir ci contre) Considérons la parallèle à « y ‘y »à la
distance « AM = x » Le moment d’inertie « I » du rectangle
« ABNM » est fonction de « x ». Cherchons la dérivée de cette fonction et , pour cela, donnons à x » un très petit
accroissement « Le moment d’inertie « I » s’augmente
d’une quantité « Donc :
Et , comme ce rapport est
indépendant de « «
lim. |
|
|
|
|
|
La dérivée du moment d’inertie étant « b
x² » on a , en remontant à la fonction
primitive : |
|
||
|
|
D’ailleurs ,
la constante « C » est nulle , car pour « x = 0 » , on a
« I = 0 » |
|
||
|
|
Pour avoir le moment d’inertie du rectangle
« ABCD3, on doit remplacer « x » par « a » dans
l’expression de « I » , ce qui
donne : « |
|
||
|
|
Exercice 2 |
|
||
|
|
Chercher le moment
d’inertie de la surface d’un cercle de rayon R par rapport à son centre .
Le moment d’inertie « I » d’un cercle
concentrique de rayon « x » est une fonction de « x ». Cherchons la dérivée de cette fonction et pour cela , donnons à « x » un petit
accroissement « Le moment d’inertie « I » s’augmente
d’une quantité « On a donc : |
|
|
|
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|||
|
|
|
|
||
|
|
CONTRÔLE |
|
||
|
|
Voir le cours !!!!! |
|
||
|
|
|
|
||
|
|
EVALUATION :
|
|
||
|
|
|
|
||
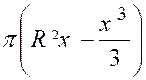
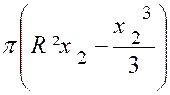
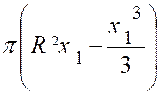
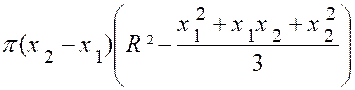
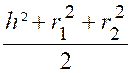
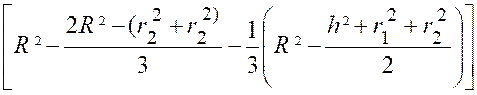
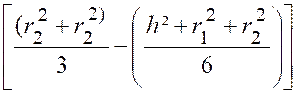
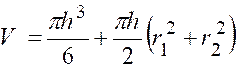

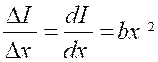 »
»
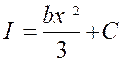
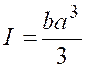 »
»