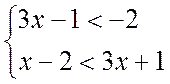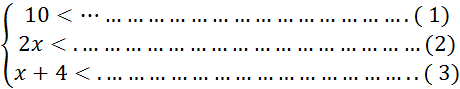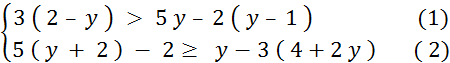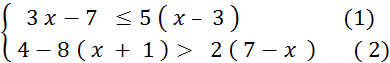|
|
Classe de 3ème |
|
|
|
|
|
|
|
|
|
|
|
Pas de corrigé |
|
Les Segments et droites graduées |
|
|
Les intervalles |
|
|
Les demi droites |
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant : 1°) Suite sur les systèmes d’inégalités du premier
degré à une inconnue |
|
|
Classe de 3ème . |
|
|
|
DOSSIER : SYSTEME d’ INEQUATIONS du premier degré à une inconnue |
|
|
|
|
|
|
|
|
|
|
TEST |
COURS
|
Interdisciplinarité Info
>>>> INTERDISCIPLINARITE
|
|
|
|
Fiche de travail |
|
|
|
|
|
Problème : |
|
||
|
|
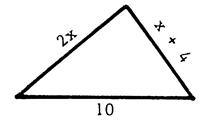
On veut construire un
triangle dont l’un des côtés est égal
à 10 cm et tel que « x » étant un nombre positif
, les autres côtés , les autres côtés aient pour longueur ( en cm )
« Quelles valeurs peut-on donner à « x » pour que
le triangle existe ? |
|
|
|
|
|
|
|
||
|
|
Le triangle existe à
condition que la longueur de chacun
des côtés soit inférieure à la somme des longueurs des deux autres côtés soit inférieure à la
somme des longueurs des deux autres côtés ( voir le cours
de collège précédent ) et ( inégalité …..) |
|
||
|
|
|
|
||
|
|
Ø On vous demande de résoudre chacune de ces
inéquations : |
|
||
|
|
Résolutions de (1) |
|
|
|
|
|
Résolutions de (2) |
|
|
|
|
|
Résolutions de (3) |
|
|
|
|
|
|
|
|
|
|
|
Ø Cherchons les solutions communes à ces trois
inéquations. Pour cela , plaçons les solutions de chacune
des inéquations sur la droite graduée. « |
|
||
|
|
« |
|
||
|
|
« |
|
||
|
|
« |
|
||
|
|
|
|
||
|
|
Ø Les solutions sont donc les nombres
strictement compris entre ……………..et …………… C'est-à-dire , les nombres « |
|
||
|
|
|
|
||
|
|
Autre exemple : Voici ci-dessous deux inéquations d’inconnue «
Chercher l’ensemble des solutions communes à
ces deux inéquations se dit aussi : Résoudre le système d’inéquations
|
|
||
|
|
Pour résoudre ce
système, on résout séparément chacune des inéquations puis on
cherche les solutions communes. |
|
||
|
|
Résolution de (1) : |
|
||
|
|
|
|
||
|
|
Résolution de (2) : |
|
||
|
|
|
|
||
|
|
Placez les solutions
sur la droite graduée ( barrez ce qui ne convient
pas ) La partie non barrée
correspond à l’ensemble des solutions cherchées. |
|
||
|
|
|
|
||
|
|
|
|
||
|
|
Les nombres « |
|
||
|
|
|
|
||
|
|
Activité en ++ :Résolvez le système d’inéquations |
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
CONTROLE :
Donner la procédure qui permet de résoudre un
système d’inéquations du premier degré.
EVALUATION
Quelle valeur de
« x » vérifie le système suivant :
1°) Quelle valeur de « x » vérifie le
système suivant :
(on dit aussi )
Résoudre :