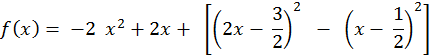utilisation des produits remarquables , problèmes,en troisième collège

 

Programme de la classe de troisième.

 

Classe de troisième collège ,

 

 

 

 

 

 

 

 

 

 

Corrigé à faire…(faire la demande)….

Pré Requis:  

Définition "identité"

Boule verte

Les égalités   EG1             

Boule verte

Les égalités   EG2             

Boule verte

Développer

Boule verte

Les éléments et ensembles 

Boule verte

Environnement du cours :

warmaths       Boule verte

Objectif précédent   Sphère metallique

 

Classe de 4ème : développer..

Classe de 3ème développer-factoriser,….

Objectif suivant : Sphère metallique

 

Les produits remarquables (application newton)

 

 Cours de niveau 4  les identités remarquables , utilisation( lycée )

INFO liste des cours proposés   Sphère metallique

Ou  autre : Sphère metallique

 

Voir : les identités  (ou produits) remarquables en 3ème collège.

 

 

Fiches sur : Utilisation des    PRODUITS  REMARQUABLES  .

 

 

 

 

 

Fiche 1 : Résolution d’un problème.

 

 

Fiche 2 : Exercice de factorisation.

 

 

Fiche 3 : Résolution d’équations.

 

 

Fiches 4 : Exercices types. Aucun corrigé disponible ….

 

 

Fiche 5 : Situations problèmes.

 

 

 

 

TEST

           FilesOfficeverte

COURS

                FilesOfficeverte

Devoir contrôle FilesOfficeverte

Devoir évaluation FilesOfficeverte

Interdisciplinarité

                        Filescrosoft Officeverte

 

Corrigé Contrôle  FilesOfficeverte

Corrigé évaluation  FilesOfficeverte

 

 

 

Fiche 1 : Résolution d’un problème.

 

 

 

 

 

 

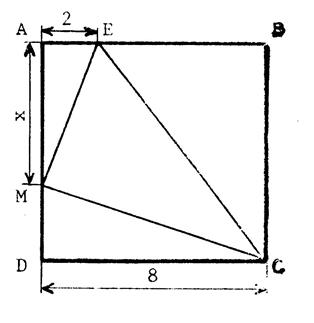
« ABCD » est un carré de 8 m de côté . « E » est un point de «[ AB ]»  tel que « AE = 2 m ».

« M » est un point de «[ AD ]»  .

On désignera  par «  » la longueur de « AM ».

 

1°) Calculons  EC² puis EM² et MC² en fonction de «  ».

pr002

 

 

 

 

 

a)      Dans le triangle « EBC », grâce au triangle de Pythagore : EC² = EB² + BC² . C'est-à-dire :  EC²  = 36 + ……= ………..

b)      Dans le triangle « ……….», grâce au triangle de Pythagore : EM² = ……………………………………………………. ……….. C'est-à-dire :  EM²  = ………… + ……= ………..

c)      Dans le triangle « ……….», grâce au triangle de Pythagore : MC ² = ……………………………………………………. C'est-à-dire :  MC ²  = ……….. + …………= ………..

 

 

 

 

 

2°) Cherchons pour quelles valeurs  de «  » , le triangle « EMC » est rectangle en « E ».

 

 

 

Mise en équation : « EMC » est un triangle  en « E » se traduit par  «  MC² = …………+ …..……. »

En remplaçant par les valeurs  du « 1° » on obtient        ( 8 – x ) ² + 64  = …………

 

Résolution de l’équation : vous transposez : ……………………………………………………………..

 

Voyez-vous une factorisation possible ? …………………………………………

Vous remarquez qu’en développant , après réduction , les …………………disparaissent .

 

Développez  ( utilisez les produits remarquables ) : ……………………………………………………………..

Réduisez les termes semblables : ……………………………………………..d’où la solution : ………………….

 

Réponse : Le triangle « EMC » est rectangle en « E » quand   AM = ………….m.

 

 

 

 

 

 

3°) Cherchons pour quelles valeurs  de « » , le triangle « EMC » est rectangle en « M ».

 

 

 

Mise en équation : « EMC » est un triangle  en « M » se traduit par  « …………+ …..……. = EC ²  »

En remplaçant par les valeurs  du « 1° » on obtient           = ………………………….……

 

Résolution de l’équation : vous transposez : ……………………………………………………………..

 

Développez :………………. …………………………………………

Vous remarquez qu’en développant , après réduction , les …………………disparaissent .

 

Réduisez les termes semblables : ……………………………………………..

 

Cette équation est de la forme «  a x + b = 0 »       , savez- vous la résoudre ? ………………………

 

Vous pouvez mettre « 2 » en facteur :     2 ( ………………………………..) = 0

Cette équation a pour solution unique : …………………………………………..

 

Réponse : Le triangle « EMC » est rectangle en « M » quand   AM = ………….m.

 

 

 

 

 

 

4°) Cherchons pour quelles valeurs  de « » , le triangle « EMC » est isocèle  de base  [ ME ] .

 

 

 

 

 

Mise en équation : « « EMC » est un triangle  isocèle de base [ ME ] » se traduit  «  MC = EC »

 

Nous allons chercher les valeurs de  « » pour lesquelles  MC² = EC²   et nous prendrons celles qui conviennent pour «  MC = EC » .

MC² = EC²   s’écrit   «  ( 8 – x ) ²  + 64 = 100 .   

Résolution de l’équation : vous transposez : ……………………………………………………………..

 

Développez :………………. …………………………………………

Réduisez les termes semblables : ………………………………………………………………..

 

Savez – vous résoudre cette équation ? …………………………………

Au lieu de développer effectuons seulement « 64 – 100  »

 

On obtient          ( 8 – x ) ² - ………………….= 0   c'est-à-dire    ( 8 – x ) ²  - ………………²  =  0.

 

En factorisant , on obtient :  (……………………..) ( ……………………) = 0 , c'est-à-dire  …………………………………………

 

L’équation a alors pour solutions : …………………………………………………………………………..

« x = 14 »  ne convient pas puisque « M » est un point de [ AD ]  et que  « AD = 8 »

«  x = 2 »  «  MC² = ( 8 - …..) ² + 64 = ………………………    MC = ……………………  Et   EC² = ………, EC = ………

 

Réponse : Le triangle « EMC » est isocèle  de base [ ME ] quand   AM = ………….m.

 

 

 

 

 

 

 

 

 

Fiche 2 : Exercice de factorisation.

 

 

 

 

 

 

Dans la leçon n°…1……, pour factoriser , vous avez utilisé :  «  k a  + k b =  k ( a + b )

Dans la leçon n° ….2 …….. Vous avez utilisé les produits remarquables.

Voici quelques exercices dans lesquels on combine les deux procédés.

 

 

 

Exercice 1 :

 

 

Factorisez comme dans la leçon 1 :  

 

Forme :

 

 

 

 

 

Exercice 2 :

 

 

Faites de même avec l’exercice suivant : 

 

 

 

Exercice 3 :

 

 

Factorisez :   

 

Commencez par mettre en évidence le facteur commun : (  factorisez  9 x² - 4    )

 

 

   

 

 

Exercice 4 :

 

 

Factorisez :          ( vous devez obtenir 3 facteurs )

 

 

 

 

 

Exercice 5 : 

 

 

Factorisez :  

 

 

 

 

 

 

Exercice 6 : 

 

 

Factorisez   :  

 

 

 

 

 

 

 

 

 

Fiche 3 : Résolution d’équations.

 

 

 

Pour résoudre les équations ci-dessous , vous procéderez comme dans la leçon n°…1…(fiche 6)…,

Vous transposez puis vous factorisez .

Si la factorisation n’est pas possible , vous développez et vous réduisez .

 

 

 

 

 

Exercice 1 :

Résolvez l’équation :      d’inconnue «  »

 

 

 

 

 

Exercice 2 :

Résolvez l’équation :     d’inconnue  «   »

 

 

 

 

 

Exercice 3 :

Résolvez l’équation :      d’inconnue  «   »

 

 

 

 

 

Exercice 4 :

Résolvez l’équation :     d’inconnue  «   »

 

 

 

 

 

 

Fiches 4 : Exercices types.

Aucun corrigé disponible ….

 

 

Exercice 1 :

( d’après le brevet de Bordeaux juin 88 ) 

«  » désignant un nombre quelconque, on considère la fonction «  » définie par : 

 

On vous demande de :

1°) Développer , réduire et ordonner :

2°) Factoriser   :

3°) Résoudre  les équations :   ; puis 

 

 

 

 

 

Exercice 2 :

( d’après le brevet de Limoges  82 ) 

«  » désignant un nombre quelconque, on considère la fonction «  » définie par :

 

 

On vous demande de :

1°) Développer , réduire et ordonner :

2°) Factoriser   :

3°) Résoudre  les équations :   ; puis 

 

 

 

 

 

 

Exercice 3 :

( d’après le brevet de Amiens  81 ) 

«  » désignant un nombre quelconque, on considère la fonction «  » et   «  »     définies par :

 

On vous demande de :

 

1°) Développer , réduire et ordonner : et

2°) Factoriser   : et

3°) Calculer :

4°) Résoudre  les équations :   ; puis   ;

 

 

 

 

 

 

Exercice 4 :

( d’après le brevet de Besançon  …………..) 

«  » désignant un nombre quelconque, on considère la fonction «  » et   «  »     définies par :

 

On vous demande de :

 

1°) Développer , réduire et ordonner : et

2°) Factoriser   : et

3°) Résoudre  les équations :   ; puis   ;

 

 

 

 

 

 

Exercice 5 :

( d’après le brevet de Rennes   8…… ) 

«  » désignant un nombre quelconque, on considère la fonction «  » définie par :

 

 

On vous demande de :

1°) Développer , réduire et ordonner :

2°) Factoriser   :

3°) Résoudre  les équations :   

4°) Calculez :

 

 

 

 

 

 

Exercice 6 :

( d’après le brevet de Dijon …………..) 

«  » désignant un nombre quelconque, on considère la fonction «  » et   «  »     définies par :

 

On vous demande de :

 

1°) Développer , réduire et ordonner : et

2°) Factoriser   : de deux façons :

-         En partant de l’écriture développée (question1)

-         En partant de l’écriture initiale.

 

3°)  Développer , réduire et ordonner  

4°) Factoriser  

3°) Résoudre  les équations :   ; puis   ;𝑔

 

 

 

 

 

 

Exercice 7 :

 «  » désignant un nombre quelconque, on considère la fonction «  »   définie par :

 

On vous demande de :

 

1°) Développer , réduire et ordonner : 

2°) Factoriser   : 

3°) Calculer :

4°) Résoudre  les équations :   

 

 

 

 

 

 

 

Fiche 5 : Situations problèmes.

 

 

 

 

 

 

Problème 1 : (brevet ….)

« ABCD » est un rectangle . L’unité est le « cm » ,  AB = 7  , AD = 6.

« E » est le point de [ AB ] tel que   AE = 3.

« M » est un point de [ AD ]. On pose  « AM =  » . ( «  » est un nombre tel que   )

 

1°) Calculez  « EC² »  puis « EM² » et « MC² » en fonction de «  ».

 

2°) Pour quelle valeur de « x » le triangle « EMC » est-il rectangle en « E » ?

 

 

 

 

 

 

Problème 2 :

Un enfant joue avec des pions, il essaie de les ranger en carré.

Il forme un premier carré de « x » rangées de « x » pions , il lui reste 11 pions.

Il augmente de « 1 » pion le côté du carré , il lui manque alors 4 pions.

Combien a -t-il de pions ?

 

 

   ;       ;  ;

Faire la vérification : …. ;;  

 

 

 

 

 

Problème 3  :

On considère deux surfaces carrées.

La longueur du côté du grand carré dépasse de 10 m la longueur du côté du petit carré.

L’aire du grand carré est 9 fois plus grande que celle du petit .

Quelle est la longueur du côté du petit carré ?

 

 

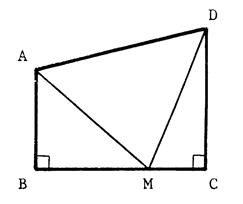
Problème 4  :

ABCD est  un trapèze rectangle ;

( BC ) est perpendiculaire à ( AB ) et à ( CD ).

AB = 7 m ; BC = 12 m ; CD = 10 m.

 

« M » est un point quelconque de  [BC].

On désigne par « x » la longueur BM.

 

Pour qu’elle valeur de « x » a – t – on  «  AM = MD » ?

pr003

 

 

 

 

 

Problème 5  :

Un carré est tel que si l’on augmente son côté de 8 cm , son aire augmente de 304 cm².

Quelle est la longueur initiale du côté du carré ?

 

 

 

 

 

 

Problème 6  :

Vous savez que le triangle dont les côtés ont pour mesures respectives  « 3 » ; « 4 » ; « 5 » est un triangle rectangle ( Vérifiez – le ) .

« 3 » ; « 4 » ; « 5 »  sont des entiers consécutifs .

Existe - -t – il d’autres triangles rectangles dont les mesures des côtés sont des entiers consécutifs ?

 

Indication :

Prenez comme inconnue l’entier du milieu et désignez  par exemple par « n » , ( .

L’entier qui le précède est alors «  »  et celui qui le suit est ……«  » 

 

 

 

 

 

 

Problème 7  :

 

 

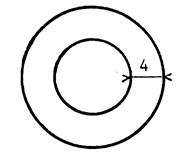
Le dessin ci-contre représente un bassin et autour de ce bassin , une allée en forme de couronne .

La largeur de la couronne est de « 4 m » et son aire  «  351,68 m² ».

Quel est le rayon du bassin ? .

( Prenez   )

pr004

 

 

 

 

 

Problème 8  :

 

 

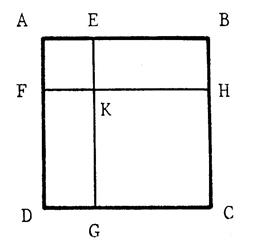
Ci-contre « ABCD » est un carré de 5 m de côté.

« E » est un point de [ AB ] et « F » un point de [ AD ] tel que «  AE = AF ».

On trace par « E »  la parallèle à ( AD ) qui coupe [DC]  en « G ».

On trace par « F »  la parallèle à ( AB ) qui coupe [BC]  en « H » et (EG) en « K ».

1°) Démontrez ( verbalement) que « AEKF » et « KHCG » sont des carrés et que « EBHK » et « FKGD » sont des rectangles.

 

2°) En appelant « x » la longueur de « AE » et de « AF », déterminez « x » pour que la somme des aires de « AEKF » et de « KHCG » soit égale à la somme des aires « EBHK » et de « FKGD ».

 

pr005

 

 

 

 

 

20 mai  15