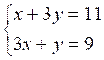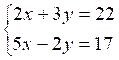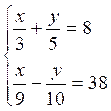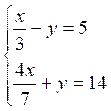@

Devoir diagnostique L tests.	
Devoir Auto - formatif (intégré au cours)	
Devoir Formatif « Contrôle : savoir » ; (remédiation)	
Devoir Formatif « Evaluation savoir faire » (remédiation)	
Devoir sommatif.	
Devoir certificatif : (remédiation)	

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°31	Problèmes à 2 inconnues : Méthode par substitution.

COURS sur :

INTERDISCIPLINARITE : Problèmes à 2 inconnues Méthode par substitution.

Quand une des deux équations est « incomplète » ou « simple » , on délaisse la « méthode par addition » ou « la méthode par soustraction » pour employer la méthode que nous allons employer dite par «substitution ».

I) Exemple.

Résoudre le système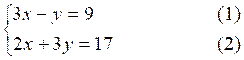

De l’équation « simple » (1) nous en tirons la valeur de « y ».

Soit 3x -9 = y (3)

On remplace « y » (valeur trouvée), dans l’équation (2)

Soit 2x + 3 (3x - 9) = 17

On développe et l’on effectue :

Soit 2x + 9x - 27 = 17

11x = 17 + 27

11x = 44

D’où

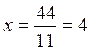
Recherche de « y » : on reporte la valeur de « x » = 4 dans l’équation (3)

Soit 3 x - 9 = y

3 ´ 4 -9 = y

12 - 9 = y

y = 3

* Faire la vérification dans l’équation (2) !!!!

II) Règle de procédure pour résoudre un système à 2 inconnues par substitution :

- rechercher si le système possède une équation « simple » ou incomplète (manque « x » ou « y »).

- Tirer la valeur d’une inconnue par rapport à l’autre dans l’équation simple ou incomplète.

- En déduire la valeur numérique de la deuxième équation (on substitue)

- Reporter cette valeur dans la formule de la première inconnue.

- Calculer la valeur de la deuxième inconnue.

Remarque :

Il faut avoir soin, avant de choisir « une » méthode et de l’appliquer, de rendre l’équation la plus simple possible. Pour cela, il faut :

- réduire au même dénominateur.

- Chasser le dénominateur commun.

- Effectuer les opérations indiquées.

- Réduire les termes semblables et simplifier.

Leçon

Algèbre : Titre

N°31

TRAVAUX d’Auto - FORMATION sur

Problèmes à 2 inconnues : Méthode par substitution

TRAVAUX N° 31 d ’ AUTO - FORMATION : CONTROLE

Compléter les phrases suivantes :

I) Avant de choisir une méthode de résolution que doit -on faire en présence du système ?

II) quand utilise- t-on la méthode par substitution ?

III) Donner la règle de procédure permettant de résoudre un système à 2 inconnues par substitution :

TRAVAUX N°31 d ‘ AUTO - FORMATION EVALUATION

Résoudre les systèmes suivants :

1
2
3
4

Problèmes :

1°) Un salarié est engagé à 3,75 euros de l’heure. Au milieu de la semaine son travail est jugé satisfaisant, le taux horaire est porté à 4 euros. Sachant qu’il a reçu 208,50 euros pour 54 heures de travail, trouver le nombre d’heures à 3,75 euros.

2°) Un marchand de fromage va au marché avec 60 kg. de fromage de deux qualités différentes. La première coûte 24 euros le kg. , la deuxième coûte 18 euros le kg. Ayant tout vendu, elle veut se rappeler de combien de fromage de la première qualité il disposait. Pour cela , il compte que le produit de sa vente s’élève à 1200 euros. Aidez le marchand à trouver ce nombre de kilogrammes

3°) Dans une fonderie, on coule 84 pièces de fonte ; les unes pèsent 8 kg. , les autres 5 kg. L’opération nécessite une masse totale de métaux de 600 kg. Quel est le nombre de pièces de chaque espèce ?

CORRIGE :

Résoudre :

Résoudre les systèmes suivants :

1
2
3
4

Problème :