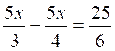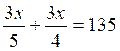|
|
|
|
|
|
ALGEBRE. N°
11 |
Information « TRAVAUX »
|
|
|
OBJECTIFS :-
médiation en algèbre. |
I )
Pré requis:
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs
« passerelle » 3ème / Seconde. |
:i |
|
i9 |
:i |
II )
ENVIRONNEMENT du dossier :
|
|
Info : |
SOMME ALGEBRIQUE.
IV)
INFORMATIONS « formation
leçon » :
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
||||
V ) DEVOIRS
( écrits):
|
Devoir diagnostique L
tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle : savoir » ; (remédiation) |
|
|
|
|
|
Devoir
sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation : ces documents
peuvent être réutilisés ( tout ou partie) pour
conclure une formation .
|
Leçon |
Titre |
|
N°11 |
SOMME ALGEBRIQUE. |
La résolution des équations plus difficiles que les précédentes
nécessite parfois l’emploi de calculs d’algèbre assez compliqués. Pour les
résoudre, il faut étudier comment se font les divers opérations algébriques,
ou, comme on dit, étudier le calcul algébrique.
Commençons par l’apprentissage de l’addition.
Avec des nombres « positifs »
I ) Premier principe.
On peut écrire : 25 + 9 + 11 + 15 = 60
Changeons les termes de place on
a encore 25 + 15 + 11 + 9 = 60
On en conclut que dans une somme on peut changer les termes de place.
|
|
a + b + c
+ d = b + a + d
+ c |
|
II ) Deuxième principe.
On peut écrire 25 + 9 + 11 + 15 = 60
On peut grouper les termes : (25 + 15) + ( 9
+ 11) = 60
Soit
40 + 20 = 60
Inversement : 40 + 20 = 60
Peut s’écrire :
( 25 + 15 ) + ( 11 + 9 ) = 60
et 25 + 9 + 11 + 15 =
60
Dans une somme, on peut regrouper les termes à volonté. On peut
également supprimer les parenthèses et disperser les termes qu’elles
renferment :
|
|
a + b + c
+ d = a +( b
+ c ) + d |
|
|
|
|
|
|
|
a + (b +
c) + d = a + d + c + b |
|
III) Applications.
1°) On peut grouper les termes de façon à obtenir des nombres
« ronds » :
4,6x + 3,75x + 5,4x + 2,25x = (4,6x + 5,4x) + (3,75x + ,25x)
= 10 x
+ 6x
= 16x
2°) On peut grouper des termes
identiques pour les additionner :
( a + b + 3c) + (
2a + b + c) = a + b+ 3c + 2a + b + c
= a + 2a + b + b + 3c + c
= 3a + 2b + 4c
|
Titre |
|
|
N°11 |
TRAVAUX d’Auto -
FORMATION sur SOMME ALGEBRIQUE. |
Enoncé les deux principes concernant la gestion des termes dans une somme
algébrique.
1°) regrouper par calcul :
|
1 |
x + 4 + 2x
+ 6 + 6x + 2 |
|
|
2 |
4,6x + 3,7 x + 5,4x + 2,25x |
|
|
3 |
15x + 7 + 27x +13 + 34x |
|
|
4 |
(x+4+9x) + (6x+6+x) |
|
|
5 |
(3a+2b+c)+(a+3b +c) |
|
|
6 |
( 5a + c +3b ) + (9c + 2b + a) |
|
Pb N°1 : 3 personnes se partagent une somme.
La première reçoit les 2/7 plus 600 € ; la seconde le 1/3 plus 700 € ;la troisième les 1 100 € restants. Quelle est la somme
partagée ?
CORRIGE :
Exercices : Résoudre les équations
suivantes :
|
1 |
18x-10 = 22 |
|
· a |
|
|
2 |
24 -3x = 9 -6 |
· b |
1,2x - 1 = 3,6 + 0,20 |
|
|
3 |
30 - 6x = 30 |
· c |
4,8 - 0,6x = 1,2 + 0,6 |
|
|
4 |
|
· |
2,4 - 0,7x = 5x - 3, 3 |
Pb N°1: Calculer le prix du mètre
d’une étoffe, sachant que la différence entre le prix de 2,75 m et celui de
1,25 m est 10,50 €.
2,75x - 1,25 x = 10,50
275x-125x=1050
11x - 5x = 42
7x = 42
x= 6
Pb N°2 : Un salarié gagne 20 € par
jour de travail, mais dépense journellement 15 €. Au bout de 43 jours, il
calcule qu’il lui manque autant de fois 1,50 € qu’il a travaillé de jours. Quel
est ce nombre de jours de travail ?
20x = somme gagné.
15 fois 43 : somme dépensée
somme
manquante : 1,5 x
20x + 1,5x = 15 fois 43
4x +0,3x = 3 fois 43
40x + 3x = 3 fois 430
43 x = 3 fois 430
x = 3 fois
10 ; x = 30